Set
Basics of Set
Subjects to be Learned
- equality of sets
- subset, proper subset
- empty set
- universal set
- power set
Contents
Definition (Equality of sets): Two sets are
equal if and only if
they have the same elements.
More formally, for any sets A and B,
A = B if and only if
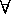 x
[ x
x
[ x
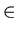 A
A
 x
x
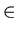 B ] .
B ] .
Thus for example {1, 2, 3} = {3, 2, 1} ,
that is the order of elements does not matter, and
{1, 2, 3} = {3, 2, 1, 1}, that is duplications do not
make any difference for sets.
Definition (Subset): A set A is a
subset of a set B if and only if
everything in A is also in B.
More formally, for any sets A and B,
A is a subset of B, and denoted by
A
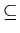 B, if and only if
B, if and only if
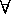 x
[ x
x
[ x
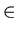 A
A
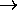 x
x
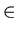 B ] .
B ] .
If
A
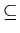 B,
and
A
B,
and
A
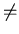 B,
then A is said to be a
proper subset
of B and it is denoted by
A
B,
then A is said to be a
proper subset
of B and it is denoted by
A
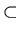 B .
B .
For example
{1, 2}
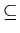 {3, 2, 1} .
{3, 2, 1} .
Also
{1, 2}
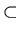 {3, 2, 1} .
{3, 2, 1} .
Definition(Cardinality): If a set S has n
distinct elements for some natural number n, n is the
cardinality (size) of S and S
is a finite set. The cardinality of S is denoted by |S|.
For example the cardinality of the set {3, 1, 2} is 3.
Definition(Empty set): A set which has no elements is called
an empty set.
More formally, an empty set, denoted by
 ,
is a set that satisfies the following:
,
is a set that satisfies the following:
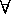 x
x
x
x
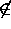
 ,
,
where
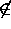 means "is not in" or "is not a member of".
means "is not in" or "is not a member of".
Note that  and
{
and
{ } are different sets.
{
} are different sets.
{ }
has one element namely
}
has one element namely  in it.
So {
in it.
So { }
is not empty.
But
}
is not empty.
But
 has nothing in it.
has nothing in it.
Definition(Universal set): A set which has all the elements in the
universe of discourse is called
a universal set.
More formally, a universal set, denoted by
U ,
is a set that satisfies the following:
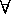 x
x
x
x
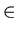 U .
U .
Three subset relationships involving empty set and universal set are listed below
as theorems without proof. Their proofs are found
elsewhere.
Note that the set A in the next four theorems are arbitrary.
So A can be an empty set or universal set.
Theorem 1: For an arbitrary set A
A
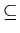 U .
U .
Theorem 2: For an arbitrary set A

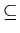 A .
A .
Theorem 3: For an arbitrary set A
A
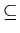 A .
A .
Definition(Power set): The set of all subsets of a set A
is called the power set of A
and denoted by
2A or
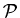 (A) .
(A) .
For example for A = {1, 2},
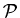 (A)
= {
(A)
= {
 ,
{1},
{2},
{1, 2} } .
,
{1},
{2},
{1, 2} } .
For B = {{1, 2}, {{1}, 2},
 } ,
} ,
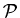 (B)
= {
(B)
= {
 ,
{{1, 2}}, {{{1}, 2}},
{
,
{{1, 2}}, {{{1}, 2}},
{ },
{ {1, 2}, {{1}, 2 }},
{ {1, 2},
},
{ {1, 2}, {{1}, 2 }},
{ {1, 2},
 },
{ {{1}, 2},
},
{ {{1}, 2},
 },
{{1, 2}, {{1}, 2},
},
{{1, 2}, {{1}, 2},
 } } .
} } .
Also
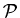 (
( )
= {
)
= { }
and
}
and
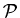 ({
({ })
= {
})
= { ,
{
,
{ }} .
}} .
Theorem 4: For an arbitrary set A,
the number of subsets of A is
2|A| .
Test Your Understanding of Basic Set Concepts
Next -- Mathematical Reasoning
Back to Schedule
Back to Table of Contents