Flow with Lower Bounds
Feasible Flow Problem with Lower Bounds:
Find a flow v that satisfies the following conditions:
 for each
for each  , where
, where  is
the set of arcs of the network.
is
the set of arcs of the network.
To solve this problem we first add an arc  of infinite capacity
to the network. Then solve the following problem:
of infinite capacity
to the network. Then solve the following problem:
Transformed Feasible Flow Problem:
Find a flow that satisfies the following conditions:
 for all
for all 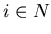 ,
,
 for all
for all  ,
,
where  is he set of arcs and
is he set of arcs and
 is the set of vertices of the network and
is the set of vertices of the network and  is defined as
is defined as
 .
.
This is the same as the feasible flow problem with no lower bounds.
A feasible flow  's for the original Feasible Flow Problem
with Lower Bounds is obtained
from this solution
's for the original Feasible Flow Problem
with Lower Bounds is obtained
from this solution  's of Transformed Feasible Flow Problem by
's of Transformed Feasible Flow Problem by
 .
.
Note that Transformed Feasible Flow Problem is obtained from
Feasible Flow Problem
with Lower Bounds
by
 .
.
Maximum Flow Problem with Lower Bounds:
Maximize flow v
subject to

 for each
for each  , where
, where  is
the set of arcs of the network.
is
the set of arcs of the network.
To solve this problem we first find a feasible flow through the network.
Then starting with that feasible flow, we solve the maximum flow problem
with the residue capacity
 .
The first term shows the remaining capacity through arc
.
The first term shows the remaining capacity through arc  and
the second term shows how much the flow from
and
the second term shows how much the flow from 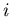 to
to  can be increased by
canceling the existing flow through arc
can be increased by
canceling the existing flow through arc  .
We can use any of the known max flow algorithms to find this maximum flow.
.
We can use any of the known max flow algorithms to find this maximum flow.


