Turing Machines
Unsolvable Problems
Subjects to be Learned
- Halting Problem
- Languages not Accepted by Turing Machines
- Other Unsolvable Problems
Contents
We have learned that deterministic Turing machines are capable of doing any computation that computers
can do, that is computationally they are equally
powerful, and that any of their variations do not exceed the computational power of
deterministic Turing machines. It is also conjectured that any "computation" human
beings perform can be done by Turing machines (Church's thesis).
In this chapter we are going to learn that there are problems that can not be solved by Turing machines
hence by computers. Here "unsolvability" is in the following sense.
First recall that solving a problem can be viewed as recognizing a language (see
Problem Solving as Language Recognition). So we are going to
look at the unsolvability in terms of language recognition.
Suppose that a language is acceptable but not decidable. Then given a string a Turing machine that
accept the language starts the computation. At any point in time, if the Turing machine is running,
there is no way of telling whether it is in an infinite loop or
along the way to a solution and it needs more time. Thus if a language is not decidable, the question
of whether or not a string is in the language may not be answered in any finite amount of time. Since
we can not wait forever for an answer, the question is unanswerable that is the problem is unsolvable.
Below we are going to see some well known unsolvable problems and see why we can say they are unsolvable.
Halting Problem
One of well known unsolvable problems is the halting problem. It asks the following question: Given an
arbitrary Turing machine M
over alphabet  = { a , b } , and an arbitrary
string w over
= { a , b } , and an arbitrary
string w over  , does M
halt when it is given w as an input ?
, does M
halt when it is given w as an input ?
It can be shown that the halting problem is not decidable, hence unsolvable.
Theorem 1 :
The halting problem is undecidable.
Proof (by M. L. Minsky):
This is going to be proven by "proof by contradiction".
Suppose that the halting problem is decidable. Then there is a Turing machine T
that solves the halting problem. That is, given a description of a Turing machine M
(over the alphabet
 ) and a string w, T writes "yes" if M
halts on w and "no"
if M
does
not halt on w, and then T halts.
) and a string w, T writes "yes" if M
halts on w and "no"
if M
does
not halt on w, and then T halts.
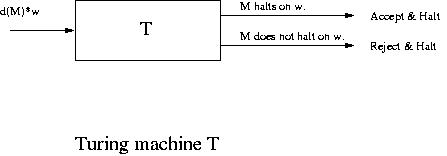
We are now going to construct the following new Turing machine Tc.
First we construct a Turing machine Tm by modifying T so that if T accepts
a string and halts, then Tm goes into an infinite loop
(Tm halts if the original T rejects a string and halts).
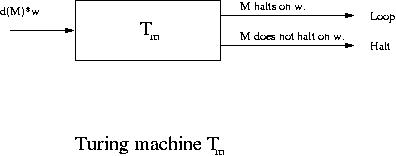
Next using Tm we are going to construct another Turing machine Tc as follows:
Tc takes as input a description of a Turing machine M, denoted by d(M), copies it
to obtain the string d(M)*d(M), where * is a symbol that separates the two copies of d(M) and then
supplies d(M)*d(M) to the Turing machine Tm .
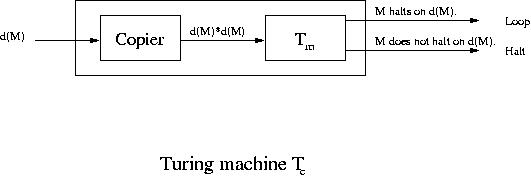
Let us now see what Tc does when a string describing Tc itself is given to it.
When Tc gets the input d(Tc) , it makes a copy, constructs the string
d(Tc)*d(Tc) and gives it to the modified T. Thus
the modified T is given a description of Turing machine Tc and the string d(Tc).
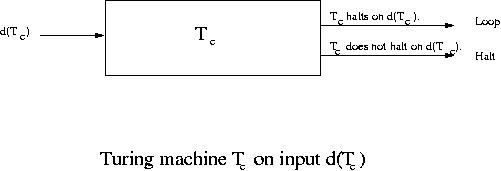
The way T was modified the modified T is going to go into an infinite loop if Tc halts on
d(Tc) and halts if Tc does not halt on d(Tc).
Thus Tc goes into an infinite loop if Tc halts on d(Tc) and it halts
if Tc does not halt on d(Tc). This is a contradiction.
This contradiction has been deduced from our assumption that there is a Turing
machine that solves the halting problem. Hence that assumption must be wrong.
Hence there is no Turing
machine
that solves the halting problem.
Program correctness and Halting Problem
Note that for any computer program a Turing machine can be constructed that
performs the task of the program. Thus the question of whether or not a program
halts for a given input is nothing but the halting problem. Thus one implication of the halting
problem is that there can be no computer programs (Turing machines) that check whether or not any
arbitrary computer
program stops for a given input.
Test Your Understanding of Unsolvable Problems
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.
Next -- More Unsolvable Preoblems
Back to Study Schedule
Back to Table of Contents
 = { a , b } , and an arbitrary
string w over
= { a , b } , and an arbitrary
string w over  , does M
halt when it is given w as an input ?
, does M
halt when it is given w as an input ?
 ) and a string w, T writes "yes" if M
halts on w and "no"
if M
does
not halt on w, and then T halts.
) and a string w, T writes "yes" if M
halts on w and "no"
if M
does
not halt on w, and then T halts.



