Turing Machines
More Unsolvable Problems
Subjects to be Learned
- Languages not Accepted by Turing Machines
- Other Unsolvable Problems
Contents
The next unsolvable problem is in a sense more difficult than the halting problem. It is presented
as a language and it can be shown that there are no Turing machines that accept the language.
Language NonSelfAccepting
Let us first define two languages NSA1 and NSA2 as follows:
NSA1 = { w | w  { a, b }*, w = d(T) for a Turing machine T and T does not accept w }
{ a, b }*, w = d(T) for a Turing machine T and T does not accept w }
NSA2 = { w | w  { a, b }*, w
{ a, b }*, w 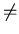 d(T) for any Turing machine T } ,
d(T) for any Turing machine T } ,
where d(T) is a description of the Turing machine T.
NSA1 is the set of strings that describe a Turing machine but that are not
accepted by the Turing machine they describe.
NSA2 is the set of strings that do not describe any Turing machine.
Neither NSA1 nor NSA2 is empty. For let T be a Turing machine that
accepts { a } and let w = d(T). Then this w is a description of a Turing machine
but it must be longer than one symbol. Hence it is not accepted by T. Hence w is
in NSA1 .
For NSA2, let w = a. Then there is no Turing machine that can be
described by the string a. Certainly more symbols than a single a are needed to describe
even the simplest Turing machine. Hence a is in NSA2 .
Thus neither NSA1 nor NSA2 is empty.
Let us define the language NonSelfAccepting as NonSelfAccepting = NSA1
 NSA2 .
Then we can prove the following theorem:
NSA2 .
Then we can prove the following theorem:
Theorem 2 There are no Turing machines that accept the language NonSelfAccepting.
Proof: This is going to be proven by contradiction.
Suppose there is a Turing machine, call it T0, that accepts NonSelfAccepting.
Let w0 = d( T0 ), that is w0
is a description of the Turing machine T0 . We are going to see
that T0 neither accepts w0 nor rejects it, which is absurd. This means
that there can not
be any Turing machine that accepts the language NonSelfAccepting.
Since NonSelfAccepting is a language, either w0 is in NonSelfAccepting or it isn't.
Hence either T0 accepts w0
or rejects it.
(1) If T0 accepts w0, then w0  NonSelfAccepting because T0 accepts NonSelfAccepting. However, by the definitions of NSA1 and NSA2, w0 is
in neither NSA1 nor NSA2 . Hence w0 is not in NonSelfAccepting .
This is a contradiction. Hence T0 can not accept w0 .
NonSelfAccepting because T0 accepts NonSelfAccepting. However, by the definitions of NSA1 and NSA2, w0 is
in neither NSA1 nor NSA2 . Hence w0 is not in NonSelfAccepting .
This is a contradiction. Hence T0 can not accept w0 .
(2) If T0 does not accept w0 , then w0 is not in NonSelfAccepting because T0 accepts NonSelfAccepting. But w0 = d( T0 ) because that is how we selected w0 . Also T0 does not accept w0 . Hence by the definition of NSA1 , w0 is in NSA1 . Hence it
is in SelfAccepting . This is again a contradiction.
Thus there can not be Turing machine T0 that accepts the language SelfAccepting .
Knowing the unsolvability of the halting problem some other problems can be shown to be unsolvable.
Problem Accepts( )
)
The problem Accepts( ) asks whetehr or not a given Turing
machine T accepts
) asks whetehr or not a given Turing
machine T accepts  .
It can be shown to be unsolvable.
.
It can be shown to be unsolvable.
Suppose that Accepts( ) is solvable.
Then there is a Turing machine that solves it. Let A be a Turing machine
that solves Accepts(
) is solvable.
Then there is a Turing machine that solves it. Let A be a Turing machine
that solves Accepts( ).
We are going to show that the halting problem becomes solvable using this A.
).
We are going to show that the halting problem becomes solvable using this A.
Let a Turing machine T' and a string w be an instance of the halting
problem. Consider a Turing machine T = TwT', where machine Tw is a
Turing machine that writes w. This T halts on  if and only
if T' halts on w.
Using this T, a Turing machine, call it M, that solves the halting problem can be
constructed as follows:
if and only
if T' halts on w.
Using this T, a Turing machine, call it M, that solves the halting problem can be
constructed as follows:
Given a description d(T') of a Turing machine T' and a string w as inputs, which is
an instance of the halting problem, M writes
the string d( T ) on the tape and let A take over.
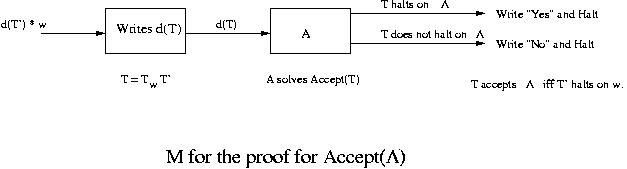
Then M halts on d(T') and w if and only if T' halts on w. That is, M solves the halting
problem. Thus if
Accepts( ) is solvable, the halting problem can be solved.
Since the halting problem is unsolvable, this means that
Accepts(
) is solvable, the halting problem can be solved.
Since the halting problem is unsolvable, this means that
Accepts( ) is unsolvable.
) is unsolvable.
Using a similar idea the following problem can also be shown to be unsolvable.
Problem AcceptsEverything
The problem AcceptsEverything asks whether or not a given Turing machine T halts on
every string over a given alphabet
 .
.
Suppose that AcceptsEverything is solvable. Let A be a Turing machine that solves
AcceptsEverything. We are going to show that Accepts( )
can be solved using the solution to it.
)
can be solved using the solution to it.
Let T' be an instance of Accepts( ).
Then consider the Turing machine T = TeraseT' , where Terase is a
Turing machine that erases the input on the tape and halts. This T halts on every string
over
).
Then consider the Turing machine T = TeraseT' , where Terase is a
Turing machine that erases the input on the tape and halts. This T halts on every string
over  if and only if T1 halts on
if and only if T1 halts on
 .
.
Using this T, a Turing machine, call it M, that solves
Accepts( ) can be constructed as shown below.
) can be constructed as shown below.
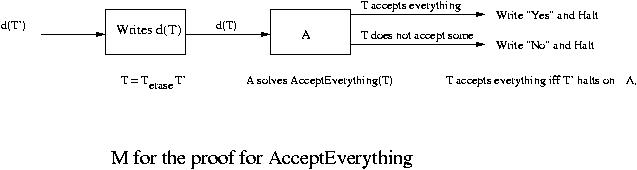
Since Accepts( ) is unsolvable, it means that
AcceptsEverything is unsolvable.
) is unsolvable, it means that
AcceptsEverything is unsolvable.
By similar arguments the following problems can be shown to be unsolvable.
AcceptsNothing
This problem asks whether or not a Turing machine accepts nothing.
It can be shown to be unsolvable using Accepts( ) .
) .
Equivalence
This problem asks whether or not two Turing machines accept the same language.
It can be shown to be unsolvable using AcceptsEverything.
Other Unsolvable Problems
Let G1 and G2 be context-free grammars and let L(G) denote the language generated by grammar G. Then the following problems are all unsolvable.
Is L( G1 )  L( G2 ) ?
L( G2 ) ?
Is L( G1 ) 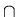 L( G2 ) =
L( G2 ) =  ? finite ? infinite ? context-free ?
? finite ? infinite ? context-free ?
Is L( G1 ) = L( G2 ) ?
Is L( G1 ) =  * ?
* ?
Is the complement of L( G1 ) context-free ?
Test Your Understanding of Unsolvable Problems
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.
Next -- Time Complexity of Problem
Back to Study Schedule
Back to Table of Contents
 { a, b }*, w = d(T) for a Turing machine T and T does not accept w }
{ a, b }*, w = d(T) for a Turing machine T and T does not accept w }
 { a, b }*, w
{ a, b }*, w 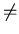 d(T) for any Turing machine T } ,
d(T) for any Turing machine T } ,
 NSA2 .
Then we can prove the following theorem:
NSA2 .
Then we can prove the following theorem:
 NonSelfAccepting because T0 accepts NonSelfAccepting. However, by the definitions of NSA1 and NSA2, w0 is
in neither NSA1 nor NSA2 . Hence w0 is not in NonSelfAccepting .
This is a contradiction. Hence T0 can not accept w0 .
NonSelfAccepting because T0 accepts NonSelfAccepting. However, by the definitions of NSA1 and NSA2, w0 is
in neither NSA1 nor NSA2 . Hence w0 is not in NonSelfAccepting .
This is a contradiction. Hence T0 can not accept w0 .
 )
)
 ) asks whetehr or not a given Turing
machine T accepts
) asks whetehr or not a given Turing
machine T accepts  .
It can be shown to be unsolvable.
.
It can be shown to be unsolvable.
 ) is solvable.
Then there is a Turing machine that solves it. Let A be a Turing machine
that solves Accepts(
) is solvable.
Then there is a Turing machine that solves it. Let A be a Turing machine
that solves Accepts( ).
We are going to show that the halting problem becomes solvable using this A.
).
We are going to show that the halting problem becomes solvable using this A.
 if and only
if T' halts on w.
Using this T, a Turing machine, call it M, that solves the halting problem can be
constructed as follows:
if and only
if T' halts on w.
Using this T, a Turing machine, call it M, that solves the halting problem can be
constructed as follows:

 ) is solvable, the halting problem can be solved.
Since the halting problem is unsolvable, this means that
Accepts(
) is solvable, the halting problem can be solved.
Since the halting problem is unsolvable, this means that
Accepts( ) is unsolvable.
) is unsolvable.
 .
.
 )
can be solved using the solution to it.
)
can be solved using the solution to it.
 ).
Then consider the Turing machine T = TeraseT' , where Terase is a
Turing machine that erases the input on the tape and halts. This T halts on every string
over
).
Then consider the Turing machine T = TeraseT' , where Terase is a
Turing machine that erases the input on the tape and halts. This T halts on every string
over  if and only if T1 halts on
if and only if T1 halts on
 .
.
 ) can be constructed as shown below.
) can be constructed as shown below.

 ) is unsolvable, it means that
AcceptsEverything is unsolvable.
) is unsolvable, it means that
AcceptsEverything is unsolvable.
 ) .
) .
 L( G2 ) ?
L( G2 ) ?
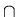 L( G2 ) =
L( G2 ) =  ? finite ? infinite ? context-free ?
? finite ? infinite ? context-free ?
 * ?
* ?