General Induction Example 4
Problem: Let s be the number of occurrences of propositional variables and truth values
(true, false) and let c
be the number of binary connectives in a proposition. Then s = c + 1 holds.
Examples: In proposition (P 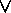 Q),
where P and Q are propositional variables,
s = 2 (P and Q), and c = 1 (
Q),
where P and Q are propositional variables,
s = 2 (P and Q), and c = 1 ( 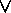 ).
In (
).
In (  (P
(P 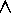 Q )
Q )
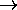 Q ),
s = 3 (P and two Q's) and c = 2
(
Q ),
s = 3 (P and two Q's) and c = 2
( 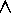 and
and
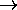 ). Note that is not a binary connective. So it is not
counted into c.
). Note that is not a binary connective. So it is not
counted into c.
Proof
First let us note that the set of propositions can be defined as follows:
Definition of Proposition (Propositional Form)
1. Basis Clause: The truth values 'true' and 'false', and all
propositional variables
such as P and Q are a proposition. Here a propositional
variable
is a variable that takes
an individual specific proposition as its value.
2. Inductive Claus: If E and F are propositions, then
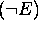 ,
,
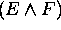 ,
,
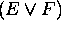 ,
,
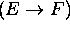 , and
, and
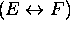 are
propositions.
are
propositions.
3. Extremal Clause: Nothing is a proposition unless it is obtained by 1. and 2.
The proof mirrors the recursive
definition of propositions.
Proof by Induction
Basis Step: Since 'true", 'false" and all propositional variables have no connectives,
s = 1 and c = 0. Hence s = c + 1 holds.
Inductive Step: Consider arbitrary propositions E and F. Let sE and
sF be the numbers of occurrences of 'true", 'false" and propositional variables
for E and F, respectively and let cE and cF be the numbers
of binary connectives for E and F, respectively.
Suppose that
sE =
cE + 1,
and
sF = cF + 1 hold. Then
(1) for ( E), s and c are the same as for E. Hence
s(
E), s and c are the same as for E. Hence
s( E) =
c(
E) =
c( E) + 1 holds.
E) + 1 holds.
(2) For (E * F), where * represents any of the binary connectives,
s(E * F) = sE +
sF, and
c(E * F) = cE + cF + 1, + 1 here being for *.
Since
sE =
cE + 1,
and
sF = cF + 1 hold,
s(E * F) = (cE + 1) + (cF + 1)
=
(cE + cF + 1) + 1
=
c(E * F) + 1
Hence s = c + 1 holds for (E * F) for any binary connective * if it holds for E
and F .
End of Inductive Step.
End of Proof.
Note that combined with the definition of propositions, this the property s = c + 1
for every proposition. Initially 'true', 'false' and propositional variables have the property
s = c + 1. Then as larger propositions are constructed following the Inductive Clause
of the definition of propositions, this property is guaranteed to be carried over to new ones
by the Inductive Step
of the proof.
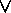 Q),
where P and Q are propositional variables,
s = 2 (P and Q), and c = 1 (
Q),
where P and Q are propositional variables,
s = 2 (P and Q), and c = 1 ( 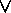 ).
In (
).
In (  (P
(P 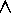 Q )
Q )
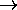 Q ),
s = 3 (P and two Q's) and c = 2
(
Q ),
s = 3 (P and two Q's) and c = 2
( 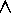 and
and
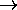 ). Note that is not a binary connective. So it is not
counted into c.
). Note that is not a binary connective. So it is not
counted into c.