Finite Automata
* of DFA and its Properties
Subjects to be Learned
- *
- Language accepted by DFA
Contents
Here we are going to formally describe what is meant by applying a transition
repeatedly, that is
the concept of *
For a state q and string w,
*( q , w ) is the state
the DFA goes into when it reads the string w starting at the state q. In general a DFA goes through
a number of states from the state q responding to the symbols in the string w.
Thus for a DFA < Q , 
,
q0 , , A > ,
the function
* :
Q 
* -> Q
is defined recursively as follows:
Definition of *:
Basis Clause: For any state q of Q , *( q ,
) = q , where denotes
the empty string.
Inducitve Clause: For any state q of Q, any string y 
* and any symbol a
,
*( q , ya ) =
( *( q , y ) , a ) .
In the definition, the Basis Clause says that a DFA stays in state q when it reads an empty string at state q
and the Inductive Clause says that the state DFA reaches after reading string ya starting at state q is the state it reaches
by reading symbol a after reading string y from state q.
Example
For example suppose that a DFA contains the transitions shown below.
Then *( q , DNR ) can be calculated as follows:
*( q , DNR )
= ( *( q , DN ) , R )
by the Inductive Clause.
= ( (
*( q , D ) , N ) , R )
by applying the Inductive Clause to *( q , DN ).
= ( (
*( q , D ) , N ) , R )
since D = D .
= ( ( (
*( q , ) , D ) , N ) , R )
by applying the Inductive Clause to
*( q , D ).
= ( (
( q , D ) , N ) , R ) ,
since ( q , ) = q .
= (
( q1 , N ) , R ) ,
since ( q , D ) = q1
as seen from the diagram.
= ( q2 , R ) ,
since ( q1 , N ) = q2
as seen from the diagram.
= q3
since ( q2 , R ) = q3
as seen from the diagram.
Properties of *
We can see the following two properties of * .
Theorem 1: For any state q of Q and any symbol a of
for a DFA < Q , ,
q0 , , A > ,
*( q , a ) =
( q , a )
Proof : Since a = a ,
*( q , a ) =
*( q , a ) .
By the definition of * ,
*( q , a ) =
(
*( q , ) , a )
But *( q , ) = q
by the definition of * .
Hence
(
*( q , ) , a ) =
( q , a ) .
The next theorem states that the state reached from any state, say q , by reading a string, say w , is the same as the state reached by first reading a prefix of w, call it x, and then by reading the rest of the w, call it y.
Theorem 2: For any state q of Q and any strings x and y over
for a DFA < Q , ,
q0 , , A > ,
*( q , xy ) =
*( *( q , x ) , y ) .
Proof : This is going to be proven by induction on string y.
That is the statement to be proven is the following:
For an arbitrary fixed string x, *( q , xy ) =
*( *( q , x ) , y ) holds for any arbitrary string y.
First let us review the recursive definition of *.
Recursive definition of *:
Basis Clause: *.
Inductive Clause: If x * and a ,
then xa * .
Extremal Clause: Nothing is in * unless it is obtained from the above two clauses.
Now the proof of the theorem.
Basis Step: If y = , then
*( q , xy ) =
*( q , x ) = *( q , x ) .
Also *( *( q , x ) , y ) =
*( *( q , x ) , ) =
*( q , x ) by the definition of
* .
Hence the theorem holds for y = .
Inductive Step: Assume that
*( q , xy ) =
*( *( q , x ) , y ) holds for an arbitrary string y. This is the induction hypothesis.
We are going to prove that
*( q , xya ) =
*( *( q , x ) , ya )
for any arbitrary symbol a of .
*( q , xya ) =
( *( q , xy ) , a ) by the definition of
*
=
( * ( *( q , x ) , y ) , a )
by the induction hypothesis.
= *( *( q , x ) , ya )
by the definition of * .
Thus the theorem has been proven.
Test Your Understanding of * of DFA and its Properties
Indicate which of the following statements are correct and which are not.
Click Yes or No , then Submit.
For the following DFA answer the questions given below.
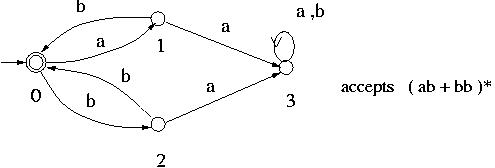
The following notations are used in the questions:
: \delta
* : \delta^*
: \Lambda
Next -- Language Accepted by DFA
Back to Study Schedule
Back to Table of Contents