Finite Automata
Conversion of NFA to DFA
Conversion of NFA to DFA
Let M2 = < Q2 ,  ,
q2,0 ,
,
q2,0 ,  2 , A2 > be an
NFA
that recognizes a language L.
Then the DFA M
= < Q,
2 , A2 > be an
NFA
that recognizes a language L.
Then the DFA M
= < Q,  ,
q0 ,
,
q0 ,  , A > that satisfies the following conditions recognizes L:
, A > that satisfies the following conditions recognizes L:
Q = 2Q2 , that is the set of all subsets of Q2 ,
q0 = { q2,0 } ,
 ( q, a ) =
( q, a ) = 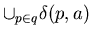 for each state q in Q and each symbol a in
for each state q in Q and each symbol a in  and
and
A = { q  Q | q
Q | q 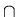 A2
A2
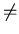
 }
}
To obtain a DFA M = < Q,  ,
q0 ,
,
q0 ,  , A > which accepts the same language as the given
NFA
M2 = < Q2 ,
, A > which accepts the same language as the given
NFA
M2 = < Q2 ,  ,
q2,0 ,
,
q2,0 ,  2 , A2 > does,
you may proceed as follows:
2 , A2 > does,
you may proceed as follows:
Initially Q =  .
.
First put { q2,0 } into Q. { q2,0 } is the initial state of the DFA M.
Then for each state q in Q do the following:
add the set 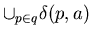 , where
, where  here is that of NFA M2,
as a state to Q if it is not already in Q for each symbol a
in
here is that of NFA M2,
as a state to Q if it is not already in Q for each symbol a
in  .
.
For this new state, add
 ( q, a ) =
( q, a ) =
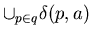 to
to
 , where the
, where the  on the right hand side
is that of NFA M2.
on the right hand side
is that of NFA M2.
When no more new states can be added to Q, the process terminates. All the states of Q that contain
accepting states of M2 are accepting states of M.
Note: The states that are not reached from the initial state are not included in Q obtained by this procedure.
Thus the set of states Q thus obtained is not necessarily equal to 2Q2 .
Example 1: Let us convert the following NFA
to DFA.
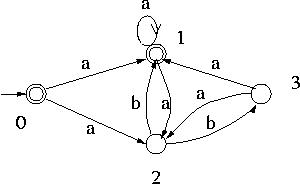
Initially Q is empty.
Then since the initial state of the DFA is {0} , {0} is added to Q.
Since  2( 0 , a ) = { 1 , 2 } ,
{ 1 , 2 } is added to Q and
2( 0 , a ) = { 1 , 2 } ,
{ 1 , 2 } is added to Q and  ( { 0 } , a ) =
{ 1 , 2 } .
( { 0 } , a ) =
{ 1 , 2 } .
Since  2( 0 , b ) =
2( 0 , b ) =
 ,
,
 is added to
Q and
is added to
Q and  ( { 0 } , b ) =
( { 0 } , b ) =
 .
.
At this point Q = { {0} , { 1 , 2 },
 } .
} .
Then since { 1 , 2 } is now in Q, the transitions from { 1 , 2 } on symbols a and b are computed.
Since  2( 1 , a ) = { 1 , 2 } , and
2( 1 , a ) = { 1 , 2 } , and
 2( 2 , a ) =
2( 2 , a ) =  ,
,
 ( { 1 , 2 } , a ) = { 1 , 2 } .
Similarly
( { 1 , 2 } , a ) = { 1 , 2 } .
Similarly  ( { 1 , 2 } , b ) = { 1 , 3 } . Thus { 1 , 3 } is added to Q .
( { 1 , 2 } , b ) = { 1 , 3 } . Thus { 1 , 3 } is added to Q .
Similarly  ( { 1 , 3 } , a ) = { 1 , 2 } and
( { 1 , 3 } , a ) = { 1 , 2 } and
 ( { 1 , 3 } , b ) =
( { 1 , 3 } , b ) =  .
Thus
no new states are added to Q . Since the transitions from all states of Q have been
computed and no more states are added to Q, the conversion process stops here.
.
Thus
no new states are added to Q . Since the transitions from all states of Q have been
computed and no more states are added to Q, the conversion process stops here.
Note that there are no states of Q2 in  .
Hence there are no states that M2 can go to from
.
Hence there are no states that M2 can go to from  .
Hence
.
Hence  (
(
 , a ) =
, a ) =
 (
(
 , b ) =
, b ) =
 .
.
For the accepting states of M, since states 0 and 1 are the accepting states of the NFA, all the states of
Q that contain 0 and/or 1 are accepting states. Hence { 0 }, { 1 , 2 } and { 1 , 3 } are the accepting
states of M.
The DFA thus obtained is shown below.
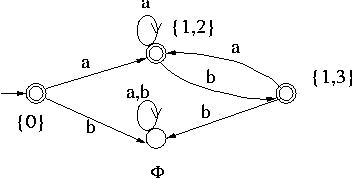
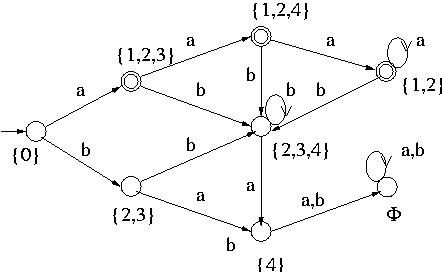
Example 2: Similarly the NFA
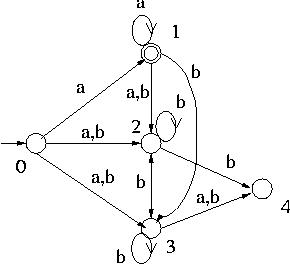
is converted to the following DFA:
Test Your Understanding of Conversion of NFA to DFA
Indicate which of the following statements are correct and which are not.
Click Yes or No , then Submit.
There are two sets of questions.
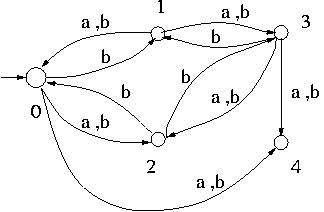
Answer the questions below on converting the following NFA
to DFA.
The following notation is used in the questions:
 : \delta
: \delta
Next -- Equivalence of NFA- andf NFA
andf NFA
Back to Study Schedule
Back to Table of Contents
 andf NFA
andf NFA  ,
q2,0 ,
,
q2,0 ,  2 , A2 > be an
NFA
that recognizes a language L.
Then the DFA M
= < Q,
2 , A2 > be an
NFA
that recognizes a language L.
Then the DFA M
= < Q,  ,
q0 ,
,
q0 ,  , A > that satisfies the following conditions recognizes L:
, A > that satisfies the following conditions recognizes L:
 ( q, a ) =
( q, a ) = 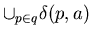 for each state q in Q and each symbol a in
for each state q in Q and each symbol a in  and
and
 Q | q
Q | q 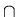 A2
A2
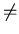
 }
}
 ,
q0 ,
,
q0 ,  , A > which accepts the same language as the given
NFA
M2 = < Q2 ,
, A > which accepts the same language as the given
NFA
M2 = < Q2 ,  ,
q2,0 ,
,
q2,0 ,  2 , A2 > does,
you may proceed as follows:
2 , A2 > does,
you may proceed as follows:
 .
.
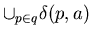 , where
, where  here is that of NFA M2,
as a state to Q if it is not already in Q for each symbol a
in
here is that of NFA M2,
as a state to Q if it is not already in Q for each symbol a
in  .
.
 ( q, a ) =
( q, a ) =
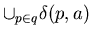 to
to
 , where the
, where the  on the right hand side
is that of NFA M2.
on the right hand side
is that of NFA M2.

 2( 0 , a ) = { 1 , 2 } ,
{ 1 , 2 } is added to Q and
2( 0 , a ) = { 1 , 2 } ,
{ 1 , 2 } is added to Q and  ( { 0 } , a ) =
{ 1 , 2 } .
( { 0 } , a ) =
{ 1 , 2 } .
 2( 0 , b ) =
2( 0 , b ) =
 ,
,
 is added to
Q and
is added to
Q and  ( { 0 } , b ) =
( { 0 } , b ) =
 .
.
 } .
} .
 2( 1 , a ) = { 1 , 2 } , and
2( 1 , a ) = { 1 , 2 } , and
 2( 2 , a ) =
2( 2 , a ) =  ,
,
 ( { 1 , 2 } , a ) = { 1 , 2 } .
Similarly
( { 1 , 2 } , a ) = { 1 , 2 } .
Similarly  ( { 1 , 2 } , b ) = { 1 , 3 } . Thus { 1 , 3 } is added to Q .
( { 1 , 2 } , b ) = { 1 , 3 } . Thus { 1 , 3 } is added to Q .
 ( { 1 , 3 } , a ) = { 1 , 2 } and
( { 1 , 3 } , a ) = { 1 , 2 } and
 ( { 1 , 3 } , b ) =
( { 1 , 3 } , b ) =  .
Thus
no new states are added to Q . Since the transitions from all states of Q have been
computed and no more states are added to Q, the conversion process stops here.
.
Thus
no new states are added to Q . Since the transitions from all states of Q have been
computed and no more states are added to Q, the conversion process stops here.
 .
Hence there are no states that M2 can go to from
.
Hence there are no states that M2 can go to from  .
Hence
.
Hence  (
(
 , a ) =
, a ) =
 (
(
 , b ) =
, b ) =
 .
.




 : \delta
: \delta
 andf NFA
andf NFA