Finite Automata
Language Accepted by NFA-
Subjects to be Learned
 -closure
-closure
 * for NFA-
* for NFA-
- Language accepted by NFA-

- Properties of
 *
*
Contents
To formally define  *
for NFA-
*
for NFA- , we start with the concept
of
, we start with the concept
of  -closure for a state which is
the set of states reachable from the state without reading any symbol.
Using that concept we define
-closure for a state which is
the set of states reachable from the state without reading any symbol.
Using that concept we define  *
and then strings and languqges accepted by NFA-
*
and then strings and languqges accepted by NFA- .
.
Definition of  -closure
-closure
Let < Q ,  ,
q0 ,
,
q0 ,  , A > be
an NFA-
, A > be
an NFA- .
Let us denote the
.
Let us denote the  -closure of a set S of states of Q
by
-closure of a set S of states of Q
by  ( S ). Then
( S ). Then  ( S )
is defined recursively as follows:
( S )
is defined recursively as follows:
Basis Clause: S 
 ( S )
( S )
Inductive Clause: For any state q of Q, if q 
 ( S ) , then
( S ) , then  ( q ,
( q ,  )
) 
 ( S ) .
( S ) .
Extremal Clause: Nothing is in  ( S ) unless it is obtained by the above two clauses.
( S ) unless it is obtained by the above two clauses.
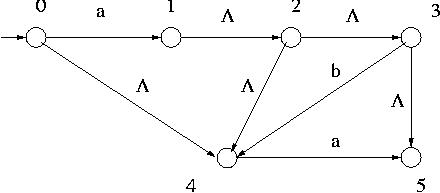
For the NFA- of the above figure,
of the above figure,
 ( { 2 } ) is obtained as follows:
( { 2 } ) is obtained as follows:
First { 2 } 
 ( { 2 } ) ,
that is, 2
( { 2 } ) ,
that is, 2 
 ( { 2 } ) .
Then since 2
( { 2 } ) .
Then since 2 
 ( { 2 } ) , by the Inductive Clause,
( { 2 } ) , by the Inductive Clause,
 ( 2 ,
( 2 ,  )
) 
 ( { 2 } ) .
( { 2 } ) .
Since  ( 2 ,
( 2 ,  ) = { 3 , 4 }, we now have { 2 , 3 , 4 }
) = { 3 , 4 }, we now have { 2 , 3 , 4 }

 ( { 2 } ) .
( { 2 } ) .
Since 3 and 4 have been added to  ( { 2 } ) ,
( { 2 } ) ,
 ( 3 ,
( 3 ,  ) = { 5 }
and
) = { 5 }
and  ( 4 ,
( 4 ,  ) =
) =
 must be included in
must be included in
 ( { 2 } ) .
Thus now { 2 , 3 , 4 , 5 }
( { 2 } ) .
Thus now { 2 , 3 , 4 , 5 } 
 ( { 2 } ) .
( { 2 } ) .
Though 5 has become a memeber of the closure,
since  ( 5 ,
( 5 ,
 ) is empty, no new members are added to
) is empty, no new members are added to
 ( { 2 } ) .
Since
( { 2 } ) .
Since  ( q ,
( q ,
 ) has been examined for all the states currently in
) has been examined for all the states currently in
 ( { 2 } ) and no more elements are added to it,
this process of generating the
( { 2 } ) and no more elements are added to it,
this process of generating the  closure terminates
and
closure terminates
and
 ( { 2 } ) = { 2 , 3 , 4 , 5 } is obtained.
( { 2 } ) = { 2 , 3 , 4 , 5 } is obtained.
As we can see from the example,  ( S )
is the set of states that can be reached from the states of S by traversing
any number of
( S )
is the set of states that can be reached from the states of S by traversing
any number of  arcs. That is, it is the set of states
that can be reached from the states of S without reading any symbols
in
arcs. That is, it is the set of states
that can be reached from the states of S without reading any symbols
in  .
.
Now with this  -closure, we can define
-closure, we can define
 * recursively as follows:
* recursively as follows:
As in the cases of DFA and NFA,  *
gives the result of applying the transition function
*
gives the result of applying the transition function  repeatedly as dictated by the given string.
repeatedly as dictated by the given string.
Definition of  *
*
 * is going to be defined recursively.
* is going to be defined recursively.
Let < Q ,  ,
q0 ,
,
q0 ,  , A > be an
NFA-
, A > be an
NFA- .
.
Basis Clause: For any state q of Q,
 *( q ,
*( q ,
 ) =
) =  ( { q } ) .
( { q } ) .
Inductive Clause: For any state q, a string y in  * and a symbol a in
* and a symbol a in  ,
,
 *( q , ya ) =
*( q , ya ) =
 (
( 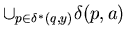 ) .
) .
What the Inductive Clause means is that
 *( q , ya ) is obtained by first
finding the states that can be reached from q by reading y
(
*( q , ya ) is obtained by first
finding the states that can be reached from q by reading y
(  *( q , y ) ), then
from each of those states p by reading a
(i.e. by finding
*( q , y ) ), then
from each of those states p by reading a
(i.e. by finding  ( p , a ) ), and then by reading
( p , a ) ), and then by reading
 's
( i.e. by taking the
's
( i.e. by taking the
 closure of the
closure of the
 ( p , a )'s ) .
( p , a )'s ) .
Example : For the NFA- of the following figure,
of the following figure,  *( 0 , ab ) can be
obtained as below:
*( 0 , ab ) can be
obtained as below:
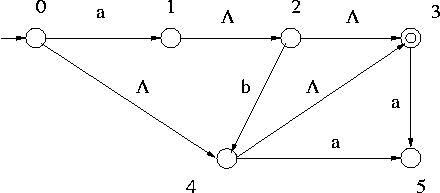
First let us compute
 *( 0 , a ) .
*( 0 , a ) .
For that we need  ( { 0 } ).
( { 0 } ).
Since it is the set of states reached by traversing the  arcs from state 0,
arcs from state 0,  ( { 0 } ) = { 0 , 3 , 4 } .
( { 0 } ) = { 0 , 3 , 4 } .
Next from each of the states in  ( { 0 } ) we read symbol
a and move to another state
(i.e. apply
( { 0 } ) we read symbol
a and move to another state
(i.e. apply  ). They are
). They are
 ( 0 , a ) = { 1 } ,
( 0 , a ) = { 1 } ,
 ( 3 , a ) =
( 3 , a ) =
 ( 4 , a ) = { 5 }.
( 4 , a ) = { 5 }.
Hence 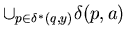 = { 1 , 5 } for q = 0 .
= { 1 , 5 } for q = 0 .
We then traverse the  arcs from
{ 1 , 5 } to get to the states in
arcs from
{ 1 , 5 } to get to the states in
 *( 0 , a ) .
Since
*( 0 , a ) .
Since
 ( { 1 } ) = { 1 , 2 , 3 } and
( { 1 } ) = { 1 , 2 , 3 } and
 ( { 5 } ) = { 5 } ,
( { 5 } ) = { 5 } ,
 *( 0 , a ) = { 1 , 2 , 3 , 5 } .
*( 0 , a ) = { 1 , 2 , 3 , 5 } .
Then to find  *( 0 , ab )
read b from each of the states in
*( 0 , ab )
read b from each of the states in  *( 0 , a ) and then take the
*( 0 , a ) and then take the
 arcs from there.
arcs from there.
Now  ( 1 , b ) ,
( 1 , b ) ,  ( 3 , b ) and
( 3 , b ) and  ( 5 , b ) are empty sets, and
( 5 , b ) are empty sets, and
 ( 2 , b ) = { 4 } .
Thus
Since
( 2 , b ) = { 4 } .
Thus
Since  ( { 4 } ) = { 3 , 4 } ,
( { 4 } ) = { 3 , 4 } ,
 *( 0 , ab ) = { 3 , 4 } .
*( 0 , ab ) = { 3 , 4 } .
A string x is accepted by an NFA- < Q ,
< Q ,  ,
q0 ,
,
q0 ,  , A >
if and only if
, A >
if and only if  *( q0 , x ) contains at least one accepting state.
*( q0 , x ) contains at least one accepting state.
The language
accepted by an NFA- < Q ,
< Q ,  ,
q0 ,
,
q0 ,  , A >
is the set of strings accepted by the NFA-
, A >
is the set of strings accepted by the NFA- .
.
For example the NFA- of the figure given above accepts the language {
of the figure given above accepts the language {  , a ,
ab } .
, a ,
ab } .
Test Your Understanding of  * of NFA-
* of NFA- and its
Properties
and its
Properties
Indicate which of the following statements are correct and which are not.
Click Yes or No , then Submit.
For the following NFA- answer the questions given below.
answer the questions given below.
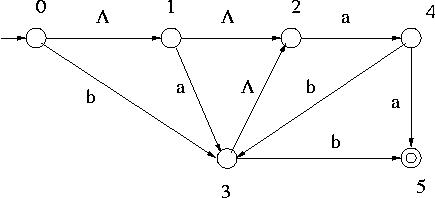
The following notations are used in the questions:
 : \delta
: \delta
 * : \delta^*
* : \delta^*
 : \Lambda
: \Lambda
Next -- Equivalence of FAs
Back to Study Schedule
Back to Table of Contents

 -closure
-closure
 * for NFA-
* for NFA-

 *
*
 *
for NFA-
*
for NFA- , we start with the concept
of
, we start with the concept
of  -closure for a state which is
the set of states reachable from the state without reading any symbol.
Using that concept we define
-closure for a state which is
the set of states reachable from the state without reading any symbol.
Using that concept we define  *
and then strings and languqges accepted by NFA-
*
and then strings and languqges accepted by NFA- .
.
 -closure
-closure
 ,
q0 ,
,
q0 ,  , A > be
an NFA-
, A > be
an NFA- .
Let us denote the
.
Let us denote the  -closure of a set S of states of Q
by
-closure of a set S of states of Q
by  ( S ). Then
( S ). Then  ( S )
is defined recursively as follows:
( S )
is defined recursively as follows:

 ( S )
( S )

 ( S ) , then
( S ) , then  ( q ,
( q ,  )
) 
 ( S ) .
( S ) .
 ( S ) unless it is obtained by the above two clauses.
( S ) unless it is obtained by the above two clauses.

 of the above figure,
of the above figure,
 ( { 2 } ) is obtained as follows:
( { 2 } ) is obtained as follows:

 ( { 2 } ) ,
that is, 2
( { 2 } ) ,
that is, 2 
 ( { 2 } ) .
Then since 2
( { 2 } ) .
Then since 2 
 ( { 2 } ) , by the Inductive Clause,
( { 2 } ) , by the Inductive Clause,
 ( 2 ,
( 2 ,  )
) 
 ( { 2 } ) .
( { 2 } ) .
 ( 2 ,
( 2 ,  ) = { 3 , 4 }, we now have { 2 , 3 , 4 }
) = { 3 , 4 }, we now have { 2 , 3 , 4 }

 ( { 2 } ) .
( { 2 } ) .
 ( { 2 } ) ,
( { 2 } ) ,
 ( 3 ,
( 3 ,  ) = { 5 }
and
) = { 5 }
and  ( 4 ,
( 4 ,  ) =
) =
 must be included in
must be included in
 ( { 2 } ) .
Thus now { 2 , 3 , 4 , 5 }
( { 2 } ) .
Thus now { 2 , 3 , 4 , 5 } 
 ( { 2 } ) .
( { 2 } ) .
 ( 5 ,
( 5 ,
 ) is empty, no new members are added to
) is empty, no new members are added to
 ( { 2 } ) .
Since
( { 2 } ) .
Since  ( q ,
( q ,
 ) has been examined for all the states currently in
) has been examined for all the states currently in
 ( { 2 } ) and no more elements are added to it,
this process of generating the
( { 2 } ) and no more elements are added to it,
this process of generating the  closure terminates
and
closure terminates
and
 ( { 2 } ) = { 2 , 3 , 4 , 5 } is obtained.
( { 2 } ) = { 2 , 3 , 4 , 5 } is obtained.
 ( S )
is the set of states that can be reached from the states of S by traversing
any number of
( S )
is the set of states that can be reached from the states of S by traversing
any number of  arcs. That is, it is the set of states
that can be reached from the states of S without reading any symbols
in
arcs. That is, it is the set of states
that can be reached from the states of S without reading any symbols
in  .
.
 -closure, we can define
-closure, we can define
 * recursively as follows:
* recursively as follows:
 *
gives the result of applying the transition function
*
gives the result of applying the transition function  repeatedly as dictated by the given string.
repeatedly as dictated by the given string.
 *
*
 * is going to be defined recursively.
* is going to be defined recursively.
 ,
q0 ,
,
q0 ,  , A > be an
NFA-
, A > be an
NFA- .
.
 *( q ,
*( q ,
 ) =
) =  ( { q } ) .
( { q } ) .
 * and a symbol a in
* and a symbol a in  ,
,
 *( q , ya ) =
*( q , ya ) =
 (
( 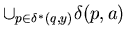 ) .
) .
 *( q , ya ) is obtained by first
finding the states that can be reached from q by reading y
(
*( q , ya ) is obtained by first
finding the states that can be reached from q by reading y
(  *( q , y ) ), then
from each of those states p by reading a
(i.e. by finding
*( q , y ) ), then
from each of those states p by reading a
(i.e. by finding  ( p , a ) ), and then by reading
( p , a ) ), and then by reading
 's
( i.e. by taking the
's
( i.e. by taking the
 closure of the
closure of the
 ( p , a )'s ) .
( p , a )'s ) .
 of the following figure,
of the following figure,  *( 0 , ab ) can be
obtained as below:
*( 0 , ab ) can be
obtained as below:

 *( 0 , a ) .
*( 0 , a ) .
 ( { 0 } ).
( { 0 } ).
 arcs from state 0,
arcs from state 0,  ( { 0 } ) = { 0 , 3 , 4 } .
( { 0 } ) = { 0 , 3 , 4 } .
 ( { 0 } ) we read symbol
a and move to another state
(i.e. apply
( { 0 } ) we read symbol
a and move to another state
(i.e. apply  ). They are
). They are
 ( 0 , a ) = { 1 } ,
( 0 , a ) = { 1 } ,
 ( 3 , a ) =
( 3 , a ) =
 ( 4 , a ) = { 5 }.
( 4 , a ) = { 5 }.
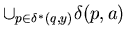 = { 1 , 5 } for q = 0 .
= { 1 , 5 } for q = 0 .
 arcs from
{ 1 , 5 } to get to the states in
arcs from
{ 1 , 5 } to get to the states in
 *( 0 , a ) .
Since
*( 0 , a ) .
Since
 ( { 1 } ) = { 1 , 2 , 3 } and
( { 1 } ) = { 1 , 2 , 3 } and
 ( { 5 } ) = { 5 } ,
( { 5 } ) = { 5 } ,
 *( 0 , a ) = { 1 , 2 , 3 , 5 } .
*( 0 , a ) = { 1 , 2 , 3 , 5 } .
 *( 0 , ab )
read b from each of the states in
*( 0 , ab )
read b from each of the states in  *( 0 , a ) and then take the
*( 0 , a ) and then take the
 arcs from there.
arcs from there.
 ( 1 , b ) ,
( 1 , b ) ,  ( 3 , b ) and
( 3 , b ) and  ( 5 , b ) are empty sets, and
( 5 , b ) are empty sets, and
 ( 2 , b ) = { 4 } .
Thus
Since
( 2 , b ) = { 4 } .
Thus
Since  ( { 4 } ) = { 3 , 4 } ,
( { 4 } ) = { 3 , 4 } ,
 *( 0 , ab ) = { 3 , 4 } .
*( 0 , ab ) = { 3 , 4 } .
 < Q ,
< Q ,  ,
q0 ,
,
q0 ,  , A >
if and only if
, A >
if and only if  *( q0 , x ) contains at least one accepting state.
*( q0 , x ) contains at least one accepting state.
 < Q ,
< Q ,  ,
q0 ,
,
q0 ,  , A >
is the set of strings accepted by the NFA-
, A >
is the set of strings accepted by the NFA- .
.
 of the figure given above accepts the language {
of the figure given above accepts the language {  , a ,
ab } .
, a ,
ab } .
 * of NFA-
* of NFA- and its
Properties
and its
Properties
 answer the questions given below.
answer the questions given below.

 : \delta
: \delta
 * : \delta^*
* : \delta^*
 : \Lambda
: \Lambda