Finite Automata
Equivalence of NFA and DFA
We are going to prove that the DFA obtained from
NFA by the conversion algorithm
accepts the same language as the NFA.
NFA that recognizes a language L is denoted by
M1 = < Q1 ,  ,
q1,0 ,
,
q1,0 ,  1 , A1 > and
DFA obtained by the conversion is denoted by M2 = < Q2,
1 , A1 > and
DFA obtained by the conversion is denoted by M2 = < Q2,
 ,
q2,0 ,
,
q2,0 ,  2 , A2 >
2 , A2 >
First we are going to prove by induction on strings that
 1*( q1,0 , w ) =
1*( q1,0 , w ) =
 2*( q2,0 , w )
for any string w. When it is proven, it obviously implies that
NFA M1 and DFA M2
accept the same strings.
2*( q2,0 , w )
for any string w. When it is proven, it obviously implies that
NFA M1 and DFA M2
accept the same strings.
Theorem: For any string w,
 1*( q1,0 , w ) =
1*( q1,0 , w ) =
 2*( q2,0 , w ) .
2*( q2,0 , w ) .
Proof: This is going to be proven by induction on w.
Basis Step: For w =  ,
,
 2*( q2,0 ,
2*( q2,0 ,
 ) = q2,0 by the definition of
) = q2,0 by the definition of
 2* .
2* .
= { q1,0 } by the construction of DFA M2 .
=  1*( q1,0 ,
1*( q1,0 ,
 ) by the definition of
) by the definition of
 1* .
1* .
Inductive Step: Assume that
 1*( q1,0 , w ) =
1*( q1,0 , w ) =
 2*( q2,0 , w )
for an arbitrary string w. --- Induction Hypothesis
2*( q2,0 , w )
for an arbitrary string w. --- Induction Hypothesis
For the string w and an arbitrry symbol a in  ,
,
 1*( q1,0 , wa ) =
1*( q1,0 , wa ) =
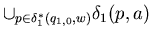
=  2(
2(
 1*( q1,0 , w ) , a )
1*( q1,0 , w ) , a )
=  2(
2(
 2*( q2,0 , w ) , a )
2*( q2,0 , w ) , a )
=  2*( q2,0 , wa )
2*( q2,0 , wa )
Thus for any string w
 1*( q1,0 , w ) =
1*( q1,0 , w ) =
 2*( q2,0 , w ) holds.
2*( q2,0 , w ) holds.
End of Proof
????
Back to Study Schedule
????
Back to Table of Contents
 ,
q1,0 ,
,
q1,0 ,  1 , A1 > and
DFA obtained by the conversion is denoted by M2 = < Q2,
1 , A1 > and
DFA obtained by the conversion is denoted by M2 = < Q2,
 ,
q2,0 ,
,
q2,0 ,  2 , A2 >
2 , A2 >
 1*( q1,0 , w ) =
1*( q1,0 , w ) =
 2*( q2,0 , w )
for any string w. When it is proven, it obviously implies that
NFA M1 and DFA M2
accept the same strings.
2*( q2,0 , w )
for any string w. When it is proven, it obviously implies that
NFA M1 and DFA M2
accept the same strings.
 1*( q1,0 , w ) =
1*( q1,0 , w ) =
 2*( q2,0 , w ) .
2*( q2,0 , w ) .
 ,
,
 2*( q2,0 ,
2*( q2,0 ,
 ) = q2,0 by the definition of
) = q2,0 by the definition of
 2* .
2* .
 1*( q1,0 ,
1*( q1,0 ,
 ) by the definition of
) by the definition of
 1* .
1* .
 1*( q1,0 , w ) =
1*( q1,0 , w ) =
 2*( q2,0 , w )
for an arbitrary string w. --- Induction Hypothesis
2*( q2,0 , w )
for an arbitrary string w. --- Induction Hypothesis
 ,
,
 1*( q1,0 , wa ) =
1*( q1,0 , wa ) =
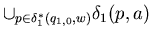
 2(
2(
 1*( q1,0 , w ) , a )
1*( q1,0 , w ) , a )
 2(
2(
 2*( q2,0 , w ) , a )
2*( q2,0 , w ) , a )
 2*( q2,0 , wa )
2*( q2,0 , wa )
 1*( q1,0 , w ) =
1*( q1,0 , w ) =
 2*( q2,0 , w ) holds.
2*( q2,0 , w ) holds.