Finite Automata
Regular Grammar
Subjects to be Learned
- Production and Grammar
- Regular Grammar
- Context-Free, Context-Sensitive and Phrase Structure Grammars
Contents
We have learned three ways of characterising regular languages:
regular expressions, finite automata and construction from simple languages
using simple operations. There is yet another way of characterizing them,
that is by something called grammar. A grammar is a set of rewrite rules
which are used to generarte strings by successively rewriting symbols.
For example consider the language represented by a+, which is
{ a, aa, aaa, . . . } .
One can generate the strings of this language by the following procedure:
Let S be a symbol to start the process with. Rewrite S using one of
the following two rules: S -> a
, and S -> aS .
These rules mean that S is rewritten as a
or as aS.
To generate the string aa for example, start with S
and apply the second rule to replace S
with the right hand side of the rule, i.e. aS, to obtain aS.
Then apply the first rule to aS to rewrite S as a.
That gives us aa.
We write S => aS to express that aS is obtained from S by applying a single production.
Thus the process of obtaining aa from S is written as S => aS => aa .
If we are not interested in the intermediate steps,
the fact that aa is obtained from S is written as S =>* aa ,
In general if a string  is obtained
from a string
is obtained
from a string
 by applying productions of a grammar G, we write
by applying productions of a grammar G, we write
 =>*G
=>*G
 and say that
and say that
 is derived from
is derived from  .
If there is no ambiguity about the grammar G
that is referred to, then we simply write
.
If there is no ambiguity about the grammar G
that is referred to, then we simply write  =>*
=>*

Formally a grammar consists of a set of nonterminals
(or variables) V, a set of terminals
 (the alphabet of the language), a start symbol S,
which ia a nonterminal, and a set of
rewrite rules (productions) P. A production has in general the form
(the alphabet of the language), a start symbol S,
which ia a nonterminal, and a set of
rewrite rules (productions) P. A production has in general the form
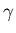 ->
->
 , where
, where 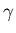 is a string of terminals and nonterminals with at least one nonterminal in it and
is a string of terminals and nonterminals with at least one nonterminal in it and
 is a string of terminals and nonterminals.
A grammar is regular if and only if
is a string of terminals and nonterminals.
A grammar is regular if and only if
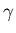 is a single
nonterminal and
is a single
nonterminal and  is a single terminal
or a single terminal followed by a single nonterminal, that is a production
is of the form X -> a or X -> aY, where X and Y are nonterminals and a is a terminal.
is a single terminal
or a single terminal followed by a single nonterminal, that is a production
is of the form X -> a or X -> aY, where X and Y are nonterminals and a is a terminal.
For example,  = {a, b}, V = { S }
and P = { S -> aS, S -> bS, S ->
= {a, b}, V = { S }
and P = { S -> aS, S -> bS, S ->  }
is a regular grammar and it generates all the strings consisting of a's and b's
including the empty string.
}
is a regular grammar and it generates all the strings consisting of a's and b's
including the empty string.
The following theorem holds for regular grammars.
Theorem 3:
A language L is accepted by an FA i.e. regular,
if L - { } can be generated by a regular grammar.
} can be generated by a regular grammar.
This can be proven by constructing an FA for the given grammar as follows:
For each nonterminal create a state. S corresponds to the initial state.
Add another state as the accepting state Z.
Then for every production X -> aY, add the transition
 ( X, a ) = Y
and for every production X -> a add the transition
( X, a ) = Y
and for every production X -> a add the transition
 ( X, a ) = Z.
( X, a ) = Z.
For example  = {a, b}, V = { S }
and P = { S -> aS, S -> bS, S -> a, S -> b } form a regular grammar
which generates the language ( a + b )+.
An NFA that recognizes this language can be obtained by creating two states S and Z,
and adding transitions
= {a, b}, V = { S }
and P = { S -> aS, S -> bS, S -> a, S -> b } form a regular grammar
which generates the language ( a + b )+.
An NFA that recognizes this language can be obtained by creating two states S and Z,
and adding transitions  ( S, a ) = { S, Z } and
( S, a ) = { S, Z } and
 ( S, b ) = { S, Z } ,
where S is the initial state and Z is the accepting state of the NFA.
( S, b ) = { S, Z } ,
where S is the initial state and Z is the accepting state of the NFA.
The NFA thus obtained is shown below.
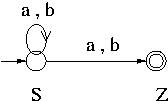
Thus L - { } is regular. If L contains
} is regular. If L contains
 as its member, then since
{
as its member, then since
{  } is regular ,
L = ( L -{
} is regular ,
L = ( L -{  } )
} )
 {
{ } is also regular.
} is also regular.
Conversely from any NFA < Q,  ,
,
 ,
q0, A > a regular grammar < Q,
,
q0, A > a regular grammar < Q,  , P,
q0 >
is obtained as follows:
, P,
q0 >
is obtained as follows:
for any a
in  , and nonterminals X and Y,
X -> aY is in P if and only if
, and nonterminals X and Y,
X -> aY is in P if and only if  (X, a) = Y ,
and for any a
in
(X, a) = Y ,
and for any a
in  and any nonterminal X,
X -> a is in P if and only if
and any nonterminal X,
X -> a is in P if and only if  (X, a) = Y
for some accepting state Y.
(X, a) = Y
for some accepting state Y.
Thus the following converse of Theorem 3 is obtained.
Theorem 4 : If L is regular i.e. accepted by an NFA,
then L - { } is generated by a regular grammar.
} is generated by a regular grammar.
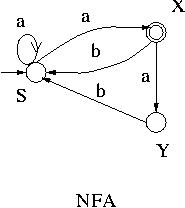
For example, a regular grammar corresponding to the NFA given below
is < Q, { a, b }, P, S > ,
where Q = { S, X, Y } , P = { S -> aS, S -> aX, X -> bS, X -> aY, Y -> bS, S -> a } .
In addition to regular languages there are three other types of languages in
Chomsky hierarchy
: context-free languages, context-sensitive languages and
phrase structure languages. They are characterized by context-free grammars,
context-sensitive grammars and phrase structure grammars, respectively.
These grammars are distinguished by the kind of productions they have
but they also form a hierarchy, that is the set of regular languages is a subset of
the set of context-free languages which is in turn a subset of the set of context-sensitive
languages
and the set of context-sensitive languages is a subset of the set of phrase structure
languages.
A grammar is a context-free grammar if and only if its
production is of the form X ->  ,
where
,
where  is a string of terminals and nonterminals,
possibly the empty string.
is a string of terminals and nonterminals,
possibly the empty string.
For example P = { S -> aSb, S -> ab } with  = { a, b }
and V = { S } is a contex-free grammar and it generates the language
{ anbn | n is a positive integer } . As we shall see later
this is an example of context-free language which is not regular.
= { a, b }
and V = { S } is a contex-free grammar and it generates the language
{ anbn | n is a positive integer } . As we shall see later
this is an example of context-free language which is not regular.
A grammar is a context-sensitive grammar if and only if its production is of the form
 1X
1X 2 ->
2 ->
 1
1
 2,
where X is a nonterminal and
2,
where X is a nonterminal and  1 ,
1 ,
 2 and
2 and
 are strings of terminals and nonterminals, possibly empty except
are strings of terminals and nonterminals, possibly empty except  .
.
Thus the nonterminal X can be rewritten as  only in the context of
only in the context of
 1X
1X 2 .
2 .
For example P = { S -> XYZS1, S -> XYZ, S1 -> XYZS1,
S1 -> XYZ, YX -> XY, ZX -> XZ, ZY -> YZ, X -> a, aX -> aa, aY -> ab,
BY -> bb, bZ -> bc, cZ -> cc } with  = { a, b, c } and V = { X, Y, Z, S, S1 } is a context-sensitive grammar
and it generates the language { anbncn | n is a positive integer } . It is an example of context-sensitive language which is
not context-free.
= { a, b, c } and V = { X, Y, Z, S, S1 } is a context-sensitive grammar
and it generates the language { anbncn | n is a positive integer } . It is an example of context-sensitive language which is
not context-free.
Context-sensitive grammars are also characterized by productions whose left hand side is not longer than the right hand side, that is, for every production
 ->
->  ,
|
,
| |
|  |
| | .
| .
For a phrase structure grammar, there is no restriction on the form of production, that is a production of a phrase structure grammar can take
the form  ->
->
 , where
, where  and
and  can be any string, but
can be any string, but  must contain at least one non-terminal.
must contain at least one non-terminal.
Test Your Understanding of Regular Grammar
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.
There are two sets of questions.
Next -- Minimization of DFA
Back to Study Schedule
Back to Table of Contents
 is obtained
from a string
is obtained
from a string
 by applying productions of a grammar G, we write
by applying productions of a grammar G, we write
 =>*G
=>*G
 and say that
and say that
 is derived from
is derived from  .
If there is no ambiguity about the grammar G
that is referred to, then we simply write
.
If there is no ambiguity about the grammar G
that is referred to, then we simply write  =>*
=>*

 (the alphabet of the language), a start symbol S,
which ia a nonterminal, and a set of
rewrite rules (productions) P. A production has in general the form
(the alphabet of the language), a start symbol S,
which ia a nonterminal, and a set of
rewrite rules (productions) P. A production has in general the form
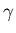 ->
->
 , where
, where 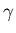 is a string of terminals and nonterminals with at least one nonterminal in it and
is a string of terminals and nonterminals with at least one nonterminal in it and
 is a string of terminals and nonterminals.
A grammar is regular if and only if
is a string of terminals and nonterminals.
A grammar is regular if and only if
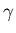 is a single
nonterminal and
is a single
nonterminal and  is a single terminal
or a single terminal followed by a single nonterminal, that is a production
is of the form X -> a or X -> aY, where X and Y are nonterminals and a is a terminal.
is a single terminal
or a single terminal followed by a single nonterminal, that is a production
is of the form X -> a or X -> aY, where X and Y are nonterminals and a is a terminal.
 = {a, b}, V = { S }
and P = { S -> aS, S -> bS, S ->
= {a, b}, V = { S }
and P = { S -> aS, S -> bS, S ->  }
is a regular grammar and it generates all the strings consisting of a's and b's
including the empty string.
}
is a regular grammar and it generates all the strings consisting of a's and b's
including the empty string.
 } can be generated by a regular grammar.
} can be generated by a regular grammar.
 ( X, a ) = Y
and for every production X -> a add the transition
( X, a ) = Y
and for every production X -> a add the transition
 ( X, a ) = Z.
( X, a ) = Z.
 = {a, b}, V = { S }
and P = { S -> aS, S -> bS, S -> a, S -> b } form a regular grammar
which generates the language ( a + b )+.
An NFA that recognizes this language can be obtained by creating two states S and Z,
and adding transitions
= {a, b}, V = { S }
and P = { S -> aS, S -> bS, S -> a, S -> b } form a regular grammar
which generates the language ( a + b )+.
An NFA that recognizes this language can be obtained by creating two states S and Z,
and adding transitions  ( S, a ) = { S, Z } and
( S, a ) = { S, Z } and
 ( S, b ) = { S, Z } ,
where S is the initial state and Z is the accepting state of the NFA.
( S, b ) = { S, Z } ,
where S is the initial state and Z is the accepting state of the NFA.

 } is regular. If L contains
} is regular. If L contains
 as its member, then since
{
as its member, then since
{  } is regular ,
L = ( L -{
} is regular ,
L = ( L -{  } )
} )
 {
{ } is also regular.
} is also regular.
 ,
,
 ,
q0, A > a regular grammar < Q,
,
q0, A > a regular grammar < Q,  , P,
q0 >
is obtained as follows:
, P,
q0 >
is obtained as follows:
 , and nonterminals X and Y,
X -> aY is in P if and only if
, and nonterminals X and Y,
X -> aY is in P if and only if  (X, a) = Y ,
and for any a
in
(X, a) = Y ,
and for any a
in  and any nonterminal X,
X -> a is in P if and only if
and any nonterminal X,
X -> a is in P if and only if  (X, a) = Y
for some accepting state Y.
(X, a) = Y
for some accepting state Y.
 } is generated by a regular grammar.
} is generated by a regular grammar.

 ,
where
,
where  is a string of terminals and nonterminals,
possibly the empty string.
is a string of terminals and nonterminals,
possibly the empty string.
 = { a, b }
and V = { S } is a contex-free grammar and it generates the language
{ anbn | n is a positive integer } . As we shall see later
this is an example of context-free language which is not regular.
= { a, b }
and V = { S } is a contex-free grammar and it generates the language
{ anbn | n is a positive integer } . As we shall see later
this is an example of context-free language which is not regular.
 1X
1X 2 ->
2 ->
 1
1
 2,
where X is a nonterminal and
2,
where X is a nonterminal and  1 ,
1 ,
 2 and
2 and
 are strings of terminals and nonterminals, possibly empty except
are strings of terminals and nonterminals, possibly empty except  .
.
 only in the context of
only in the context of
 1X
1X 2 .
2 .
 = { a, b, c } and V = { X, Y, Z, S, S1 } is a context-sensitive grammar
and it generates the language { anbncn | n is a positive integer } . It is an example of context-sensitive language which is
not context-free.
= { a, b, c } and V = { X, Y, Z, S, S1 } is a context-sensitive grammar
and it generates the language { anbncn | n is a positive integer } . It is an example of context-sensitive language which is
not context-free.
 ->
->  ,
|
,
| |
| 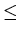 |
| | .
| .
 ->
->
 , where
, where  and
and  can be any string, but
can be any string, but  must contain at least one non-terminal.
must contain at least one non-terminal.