Turing Machines
Types of Turing Machines
Subjects to be Learned
- Variation of Turing Machine
Contents
There are a number of other types of Turing machines in addition to the one we have seen such as Turing machines with multiple tapes, ones having one tape but with multiple heads, ones with two dimensional tapes, nondeterministic Turing machines etc.
It turns out that computationally all these Turing machines are equally powerful.
That is, what one type can compute any other can also compute. However, the efficiency of computation,
that is, how fast they can compute, may vary.
Turing Machines with Two Dimensional Tapes
This is a kind of Turing machines that have one finite control, one read-write head
and one two dimensional tape. The tape has the top end and the left end but extends indefinitely
to the right and down. It is divided into rows of small squares.
For any Turing machine of this type there is a Turing machine with a one dimensional tape
that is equally powerful, that is, the former can be simulated by the latter.
To simulate a two dimensional tape with a one dimensional tape, first we map the squares of the two
dimensional
tape to those of the one dimensional tape diagonally as shown in the following tables:
Two Dimensional Tape
| v | v | v | v |
v | v | v | . . . | . . . |
h | 1 | 2 | 6 | 7 | 15 | 16 | . . . | . . . |
h | 3 | 5 | 8 | 14 | 17 | 26 | . . . | . . . |
h | 4 | 9 | 13 | 18 | 25 | . . . | . . . | . . . |
h | 10 | 12 | 19 | 24 | . . . | . . . | . . . | . . . |
h | 11 | 20 | 23 | . . . | . . . | . . . | . . . | . . . |
h | 21 | 22 | . . . | . . . | . . . | . . . | . . . | . . . |
| . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . | . . . |
Here the numbers indicate the correspondence of squares in the two tapes: square i
of the two dimensional
tape is mapped to square i of the one dimensional tape. h and
v are symbols which
are not
in the tape alphabet
and
they are used to mark the left and the top end of the tape, respectively.
One Dimensional Tape
| v | 1 | v | 2 | 3 | h | 4 | 5 | 6 | v | 7 | 8 | 9 | 10 | h | 11 | . . . | . . . |
The head of a two dimensional tape moves one square up, down, left or right.
Let us simulate this head move with a one dimensional tape.
Let i be the head position of the two dimensional tape. If the head moves down from
i, then move the head of the one dimensional tape to right until it hits h
or v counting the number of squares it has visited after i.
Let k be the number of squares visited by the head of the one dimensional tape.
If h was hit first, then from h move
the head of the one dimensional tape further right to the k-th square from h.
That is the square corresponding to the square below i in the two dimensional tape.
If v was hit first, then (k+1)-th square to the right from v is the new head
position.
For example, suppose that the head position is at 8 for the two dimensional tape in the above table,
that is i = 8. If the head moves down to position 13, then
for the one dimensional tape, the head moves from position 8 to right. Then it
meets h first, which is the third square from 8. Thus from h, move 3
positions to the right. That is the head position of the one dimensional tape corresponding to 13 on the two dimensional tape.
If i = 5 and the head moves down on the other hand, then on the one dimensional tape the
head moves to the right and it hits v first, which is the second square from
i = 5. Thus this time the third square is the head position of the one dimensional tape
corresponding to 9 on the two dimensional tape.
Similarly formulas can be found for the head position on the one dimensional tape corresponding to move
up, right or left on the two dimensional tape. Details are omitted. Thus some Turing machines with a one
dimensional tape can simulate every move of a Turing machine with one two dimensional tape. Hence they
are
at least as powerful as Turing machines with a two dimensional tape. Since
Turing machines with a two dimensional tape obviously can simulate Turing machines with a one
dimensional tape, it can be said that they are equally powerful.
Turing Machines with Multiple Tapes :
This is a kind of Turing machines that have one finite control and more than one tapes
each with its own read-write head.
It is denoted by a 5-tuple < Q ,  ,
,
 , q0,
, q0,  > .
Its transition function is a partial function
> .
Its transition function is a partial function
 : Q
: Q  (
( 
 {
{ } )n ->
( Q
} )n ->
( Q  { h } )
{ h } )  (
( 
 {
{ } )n
} )n
 { R , L , S }n .
{ R , L , S }n .
A configuration for this kind of Turing machine must show the current state the machine is in and the state
of each tape.
It can be proven that any language accepted by an n-tape Turing machine can be accepted by a one tape
Turing machine and that any function computed by an n-tape Turing machine can be computed by a one tape
Turing machine. Since the converses are obviously true, one can say that one tape Turing machines
are as powerful as n-tape Turing machines.
Turing Machines with Multiple Heads :
This is a kind of Turing machines that have one finite control and one tape but
more than one read-write heads. In each state only one of the heads is allowed to read
and write. It is denoted by a 5-tuple < Q ,  ,
,
 , q0,
, q0,  >.
The transition function is a partial function
>.
The transition function is a partial function
 : Q
: Q  { H1 , H2 ... ,
Hn }
{ H1 , H2 ... ,
Hn }  (
( 
 {
{ } ) ->
( Q
} ) ->
( Q  { h } )
{ h } )  (
( 
 {
{ }
}
 { R , L , S } ,
{ R , L , S } ,
where H1 , H2 ... ,
Hn denote the tape heads.
It can be easily seen that this type of Turing machines are as powerful as one tape Turing machines.
Turing Machines with Infinite Tape :
This is a kind of Turing machines that have one finite control and one tape
which extends infinitely in both directions.
It turns out that this type of Turing machines are only as powerful as one tape Turing machines
whose tape has a left end.
Nondeterministic Turing Machines
A nondeterministic Turing machine is a Turing machine which, like nondeterministic finite automata,
at any state it is in and for the tape symbol it is reading, can take any action selecting from a set of
specified actions rather than taking one definite predetermined action. Even in the same situation
it may take different actions at different times.
Here an action means the combination of writing a symbol on the tape, moving the tape head and going to
a next state. For example let us consider the language L = { ww : w
 { a , b }* } . Given a string x, a
nondeterministic Turing machine that accepts this language L would first guess the midpoint of x,
that is the place where the second half of x starts. Then it would compare the first half of x
with the second half by comparing the i-th symbol of the first half with the i-th symbol of the second
half for i = 1, 2, ... . A deterministic Turing machine, on the other hand, can not guess the midpoint
of the string x. It must find the midpoint by for example
pairing off symbols from either end of x.
{ a , b }* } . Given a string x, a
nondeterministic Turing machine that accepts this language L would first guess the midpoint of x,
that is the place where the second half of x starts. Then it would compare the first half of x
with the second half by comparing the i-th symbol of the first half with the i-th symbol of the second
half for i = 1, 2, ... . A deterministic Turing machine, on the other hand, can not guess the midpoint
of the string x. It must find the midpoint by for example
pairing off symbols from either end of x.
Formally a nondeterministic Turing machine is a Turing machine whose
transition function takes values that are subsets of
( Q  { h } )
{ h } )  (
( 
 {
{ }
}
 { R , L , S } .
{ R , L , S } .
As in the case of NFA, it is understood that a nondeterministic Turing machine at any configuration
selects one combination of
next state, tape symbol and head movement out of the set of triples
without following any specific
predetermined rule.
It can be shown that a nondeterministic Turing machine is only as powerful
as a deterministic Turing machine.
Theorem
Any language accepted by a nondeterministic Turing machine is also accepted by
some deterministic Turing machine.
Proof :
Let TN denote a nondeterministic Turing machine.
Given a string x , TN starts at the initial configuration and goes through a sequence of
configurations until it reaches a halt configuration , goes into an infinite loop or aborts.
At any point in the process TN is in some configuration and has a finite set of
configurations to choose from for its next configuration. The set of all possible computations that
TN can perform for a given string x can be represented by a rooted tree as follows. The root
of the tree is the
initial configuration and it is the only vertex of level 0. All possible configurations that are
reachable by applying the transition function of TN once form the children of the initial
configuration. They form level 1. In general for each vertex of level i
all possible configurations that are reachable by applying the transition function of TN
are its children. The children of all the vertices of
level i form level i+1. Note that the number of children for a vertex
in this tree is finite because
the number of states is finite and there are a finite number of tape symbols.
For example consider the following nondeterministic Turing machine that accepts
a+ .
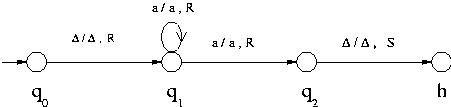
Turing machine accepting a+
Given the string aa, it would proceed as follows to accept it:
( q0 ,  aa )
aa )
 ( q1 ,
( q1 ,  aa )
aa )
 ( q1 ,
( q1 ,  aa )
aa )
 ( q2 ,
( q2 ,  aa
aa )
)
 ( h ,
( h ,  aa
aa ) .
) .
At the second and third configurations in the above sequence, it has two
candidates for the next configuration:
( q1 ,  aa ) and
( q2 ,
aa ) and
( q2 ,  aa ) for the second,
and ( q1 ,
aa ) for the second,
and ( q1 ,  aa
aa )
and
( q2 ,
)
and
( q2 ,  aa
aa ) for the third.
) for the third.
The tree for this case would be as follows:

One way to simulate a nondeterministic Turing machine, call it T1, with a deterministic one, call it T2,
is to traverse this tree breadth-first way from the root until the halt state
is reached. At each level of the tree, T2 applies the transition function of T1
to each configuration at that level and computes its children. These children are the configurations of
the next level and they are stored on the tape (if necessary a second tape may be used). If there is
the halting state among these children, then T2 accepts the string and halts. It can be
easily seen that T2 accepts a string if and only if T1 accepts it. Thus any
language accepted by a nondeterministic Turing machine is also accepted by a deterministic Turing
machine, though a deterministic Turing machine might take much more time than a nondeterministic Turing
machine to accept a string.
Many other variations of Turing machine are possible. However, it has been shown that none of them
exceed the capability of basic deterministic Turing machine
as far as accepting languages is concerned. In fact the Church's thesis
conjectures that any so called computation done by humans or computers can be
performed by a basic deterministic Turing machine.
Test Your Understanding of Different Types of Turing Machines
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.
Next -- Unsolvable Problems
Back to Study Schedule
Back to Table of Contents
 ,
,
 , q0,
, q0,  > .
Its transition function is a partial function
> .
Its transition function is a partial function
 : Q
: Q  (
( 
 {
{ } )n ->
( Q
} )n ->
( Q  { h } )
{ h } )  (
( 
 {
{ } )n
} )n
 { R , L , S }n .
{ R , L , S }n .
 ,
,
 , q0,
, q0,  >.
The transition function is a partial function
>.
The transition function is a partial function
 : Q
: Q  { H1 , H2 ... ,
Hn }
{ H1 , H2 ... ,
Hn }  (
( 
 {
{ } ) ->
( Q
} ) ->
( Q  { h } )
{ h } )  (
( 
 {
{ }
}
 { R , L , S } ,
{ R , L , S } ,
 { a , b }* } . Given a string x, a
nondeterministic Turing machine that accepts this language L would first guess the midpoint of x,
that is the place where the second half of x starts. Then it would compare the first half of x
with the second half by comparing the i-th symbol of the first half with the i-th symbol of the second
half for i = 1, 2, ... . A deterministic Turing machine, on the other hand, can not guess the midpoint
of the string x. It must find the midpoint by for example
pairing off symbols from either end of x.
{ a , b }* } . Given a string x, a
nondeterministic Turing machine that accepts this language L would first guess the midpoint of x,
that is the place where the second half of x starts. Then it would compare the first half of x
with the second half by comparing the i-th symbol of the first half with the i-th symbol of the second
half for i = 1, 2, ... . A deterministic Turing machine, on the other hand, can not guess the midpoint
of the string x. It must find the midpoint by for example
pairing off symbols from either end of x.
 { h } )
{ h } )  (
( 
 {
{ }
}
 { R , L , S } .
{ R , L , S } .
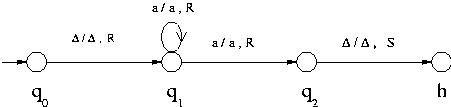
 aa )
aa )
 ( q1 ,
( q1 ,  aa )
aa )
 ( q1 ,
( q1 ,  aa )
aa )
 ( q2 ,
( q2 ,  aa
aa )
)
 ( h ,
( h ,  aa
aa ) .
) .
 aa ) and
( q2 ,
aa ) and
( q2 ,  aa ) for the second,
and ( q1 ,
aa ) for the second,
and ( q1 ,  aa
aa )
and
( q2 ,
)
and
( q2 ,  aa
aa ) for the third.
) for the third.
