Reasoning



Subjects to be Learned

Contents

Predicate logic is more powerful than propositional logic. It allows one to reason about properties and relationships of individual objects. In predicate logic, one can use some additional inference rules, which are discussed below, as well as those for propositional logic such as the equivalences, implications and inference rules.

The following four rules describe when and how the universal and existential quantifiers can be added to or deleted from an assertion.

  1. Universal Instantiation:

    x P(x)
    -------
    P(c)

    where c is some arbitrary element of the universe.


    2. Go to Universal Instantiation for further explanations and examples.

  2. Universal Generalization:

    P(c)
    ----------
    x P(x)

    where P(c) holds for every element c of the universe of discourse.


    3. Go to Universal Generalization for further explanations and examples.

  3. Existential Instantiation:

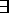    x P(x)
    -------
    P(c)

    where c is some element of the universe of discourse. It is not arbitrary but must be one for which P(c) is true.


    4. Go to Existential Instantiation for further explanations and examples.

  4. Existential Generalization:

    P(c)
    ----------
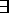    x P(x)

    where c is an element of the universe.


    5. Go to Existential Generalization for further explanations and examples.

Negation of Quantified Statement

Another important inference rule is the following:

    x P(x) x P(x)

This, for example, shows that if P(x) represnts x is happy and the universe is the set of people, then "There does not exist a person who is happy" is equivalent to "Everyone is not happy".
Thus the left side can be substituted for the right side whenever necessary in reasoning and vice versa.

Example:

As an example of inference using these rules, let us consider the following reasoning:

A check is void if it has not been cashed for 30 days. This check has not been cashed for 30 days. Therefore this check is void. You can not cash a check which is void. Therefore you can not cash this check. We now have a check which can not be cashed.

This can be put into symbolic form using the following predicates assuming the universe is the set of all objects:
C(x):  x is a check.
T(x):  x has been cashed within 30 days.
V(x):  x is void.
S(x):  x can be cashed.
This_check represents a specific object in the universe which corresponds to "this check".

x [ [ C(x)     T(x) ] V(x) ]
T( This_check )
-----------------------------------
V( This_check )

x [ [ C(x)     V(x) ] S(x) ]
-----------------------------------------------
S( This_check )
-----------------------------------------------
x [ C(x)     S(x) ] .

Here the reasoning proceeds as follows:

From x [ [ C(x)     T(x) ] V(x) ] by Universal Instantiation
[ [ C( This_check ) T( This_check ) ] V( This_check ) ]

Since This_check is a check and T( This_check ) ,
[ C( This_check ) T( This_check ) ] holds.

Hence
[ [ C( This_check ) T( This_check ) ] V( This_check ) ]
[ C( This_check ) T( This_check ) ]
---------------------------------------------------------
V( This_check )
by Modus Ponens.

Then from x [ [ C(x) V(x) ] S(x) ] by Universal Instantiation,
[ [ C( This_check ) V( This_check ) ] S( This_check ) ]

Since V( This_check ) , and C( This_check ),

[ [ C( This_check ) V( This_check ) ] S( This_check ) ]
[ C( This_check ) V( This_check ) ]
----------------------------------------------------
S( This_check )
by Modus Ponens.

Since C( This_check ) also holds,

S( This_check )
C( This_check )
----------------------------------------------------
C( This_check ) S( This_check )

Then by Existential Generalization x [ C( x ) S(x) ] .


More examples of reasoning using these rules can be found in sets.



Next -- Introduction to Sets

Back to Schedule
Back to Table of Contents