Predicate Logic
From Wff to Proposition
Subjects to be Learned
- interpretation
- satisfiable wff
- invalid wff (unsatisfiable wff)
- valid wff
- equivalence of wffs
Contents
Interpretation
A wff is, in general, not a proposition.
For example, consider the wff  x P(x).
Assume that
P(x) means that x is non-negative (greater than or equal to 0).
This wff is true
if the universe is the set {1, 3, 5}, the set {2, 4, 6}
or the set of natural numbers, for example, but it is not true if the universe is the set
{-1, 3, 5}, or the set of integers, for example.
x P(x).
Assume that
P(x) means that x is non-negative (greater than or equal to 0).
This wff is true
if the universe is the set {1, 3, 5}, the set {2, 4, 6}
or the set of natural numbers, for example, but it is not true if the universe is the set
{-1, 3, 5}, or the set of integers, for example.
Further more the wff  x Q(x, y),
where Q(x, y) means x is greater than y,
for the universe {1, 3, 5} may be true or false depending on the value of y.
x Q(x, y),
where Q(x, y) means x is greater than y,
for the universe {1, 3, 5} may be true or false depending on the value of y.
As one can see from these examples, the truth value of a wff is determined by the universe,
specific predicates assigned to the predicate variables such as P
and Q,
and the
values assigned to the
free variables. The specification of the universe and predicates,
and an assignment of a value to
each free variable in a wff is called an interpretation
for the wff.
For example, specifying the set {1, 3, 5} as the universe and assigning 0
to the variable y, for example, is an interpretation for the wff
 x Q(x, y),
where Q(x, y) means x is greater than y.
x Q(x, y),
where Q(x, y) means x is greater than y.
 x Q(x, y) with that interpretation reads,
for example, "Every number in the set {1, 3, 5} is greater than 0".
x Q(x, y) with that interpretation reads,
for example, "Every number in the set {1, 3, 5} is greater than 0".
As can be seen from the above example, a wff becomes a proposition when it is given an interpretation.
There are, however, wffs which are always true or always false under any interpretation.
Those and related concepts are discussed below.
Satisfiable, Unsatisfiable and Valid Wffs
A wff is said to be satisfiable if there exists an interpretation
that makes it true, that is if there are a universe, specific predicates assigned
to the predicate variables, and an assignment of values to the free
variables that make the wff true.
For example,  x N(x), where
N(x) means that x is non-negative, is satisfiable. For if the universe
is the set of natural numbers,
the assertion
x N(x), where
N(x) means that x is non-negative, is satisfiable. For if the universe
is the set of natural numbers,
the assertion
 x N(x) is true,
because all natural numbers are non-negative.
Similarly
x N(x) is true,
because all natural numbers are non-negative.
Similarly 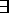 x N(x) is also satisfiable.
x N(x) is also satisfiable.
However,  x [N(x)
x [N(x) 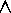
 N(x)] is not satisfiable because it can never be true.
A wff is called invalid or
unsatisfiable,
if there is no interpretation that makes it true.
N(x)] is not satisfiable because it can never be true.
A wff is called invalid or
unsatisfiable,
if there is no interpretation that makes it true.
A wff
is valid if it is true for every interpretation*.
For example, the wff
 x P(x)
x P(x) 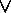
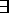 x
x  P(x)
is valid for any predicate name P ,
because
P(x)
is valid for any predicate name P ,
because
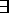 x
x  P(x)
is the negation of
P(x)
is the negation of  x P(x).
x P(x).
However, the wff
 x N(x) is satisfiable but not valid.
x N(x) is satisfiable but not valid.
Note that a wff is not valid iff it is unsatisfiable for a valid wff is equivalent to true.
Hence its negation is false.
Equivalence
Two wffs W1 and W2 are
equivalent
if and only if W1  W2
is valid, that is if and only if
W1
W2
is valid, that is if and only if
W1  W2
is true for all interpretations.
W2
is true for all interpretations.
For example  x P(x) and
x P(x) and

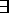 x
x
 P(x)
are equivalent for any predicate name P . So are
P(x)
are equivalent for any predicate name P . So are
 x [ P(x)
x [ P(x) 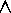 Q(x) ]
and [
Q(x) ]
and [  x P(x)
x P(x) 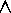
 x Q(x) ] for any predicate names
P and Q .
x Q(x) ] for any predicate names
P and Q .
*
To be precise, it is not for every interpretation but for the ones that "make sense".
For example you don't consider the universe of set of people for the predicate x > 1 as
an interpretation.
Also an interpretation assingns a specific predicate to each
predicate varialbe. A rigorous definition of interpretation etc. are, however, beyond the scope of this course.
Test Your Understanding of Equivalence etc.
Indicate which of the following statements are correct and which are not.
Click Yes or No , then Submit. There are two sets of questions.
Next -- English to Logic Translation
Back to Schedule
Back to Table of Contents
 x P(x).
Assume that
P(x) means that x is non-negative (greater than or equal to 0).
This wff is true
if the universe is the set {1, 3, 5}, the set {2, 4, 6}
or the set of natural numbers, for example, but it is not true if the universe is the set
{-1, 3, 5}, or the set of integers, for example.
x P(x).
Assume that
P(x) means that x is non-negative (greater than or equal to 0).
This wff is true
if the universe is the set {1, 3, 5}, the set {2, 4, 6}
or the set of natural numbers, for example, but it is not true if the universe is the set
{-1, 3, 5}, or the set of integers, for example.
 x Q(x, y),
where Q(x, y) means x is greater than y,
for the universe {1, 3, 5} may be true or false depending on the value of y.
x Q(x, y),
where Q(x, y) means x is greater than y,
for the universe {1, 3, 5} may be true or false depending on the value of y.
 x Q(x, y),
where Q(x, y) means x is greater than y.
x Q(x, y),
where Q(x, y) means x is greater than y.
 x Q(x, y) with that interpretation reads,
for example, "Every number in the set {1, 3, 5} is greater than 0".
x Q(x, y) with that interpretation reads,
for example, "Every number in the set {1, 3, 5} is greater than 0".
 x N(x), where
N(x) means that x is non-negative, is satisfiable. For if the universe
is the set of natural numbers,
the assertion
x N(x), where
N(x) means that x is non-negative, is satisfiable. For if the universe
is the set of natural numbers,
the assertion
 x N(x) is true,
because all natural numbers are non-negative.
Similarly
x N(x) is true,
because all natural numbers are non-negative.
Similarly 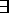 x N(x) is also satisfiable.
x N(x) is also satisfiable.
 x [N(x)
x [N(x) 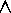
 N(x)] is not satisfiable because it can never be true.
A wff is called invalid or
unsatisfiable,
if there is no interpretation that makes it true.
N(x)] is not satisfiable because it can never be true.
A wff is called invalid or
unsatisfiable,
if there is no interpretation that makes it true.
 x P(x)
x P(x) 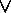
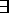 x
x  P(x)
is valid for any predicate name P ,
because
P(x)
is valid for any predicate name P ,
because
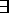 x
x  P(x)
is the negation of
P(x)
is the negation of  x P(x).
x P(x).
 x N(x) is satisfiable but not valid.
x N(x) is satisfiable but not valid.
 W2
is valid, that is if and only if
W1
W2
is valid, that is if and only if
W1  W2
is true for all interpretations.
W2
is true for all interpretations.
 x P(x) and
x P(x) and

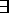 x
x
 P(x)
are equivalent for any predicate name P . So are
P(x)
are equivalent for any predicate name P . So are
 x [ P(x)
x [ P(x) 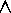 Q(x) ]
and [
Q(x) ]
and [  x P(x)
x P(x) 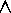
 x Q(x) ] for any predicate names
P and Q .
x Q(x) ] for any predicate names
P and Q .