1.
 ( P
( P
 Q )
Q )
 ( P
( P

 Q )
Q )
What this means is that the negation of "if P then Q" is "P but not Q". For example, if you said to someone "If I win a lottery, I will give you $100,000." and later that person says "You lied to me." Then what that person means is that you won the lottery but you did not give that person $100,000 you promised.
To prove this, first let us get rid of
 using one of the identities: ( P
using one of the identities: ( P
 Q )
Q )
 (
(  P
P
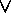 Q ).
Q ).
That is,
 ( P
( P
 Q )
Q )

 (
(  P
P
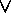 Q ).
Q ).
Then by De Morgan, it is equivalent to

 P
P

 Q , which is equivalent to
P
Q , which is equivalent to
P 
 Q,
since the double negation of a proposition is equivalent to the original proposition
as seen in the identities.
Q,
since the double negation of a proposition is equivalent to the original proposition
as seen in the identities.
2. P
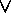 ( P
( P  Q )
Q )
 P --- Absorption
P --- Absorption
What this tells us is that P
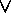 ( P
( P  Q )
can be simplified to P, or if necessary P can be expanded
into P
Q )
can be simplified to P, or if necessary P can be expanded
into P 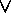 ( P
( P  Q ) .
Q ) .
To prove this, first note that P
 ( P
( P  T ).
T ).
Hence
P
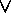 ( P
( P  Q )
Q )
 ( P
( P  T )
T )
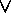 ( P
( P  Q )
Q )
 P
P
 ( T
( T 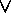 Q ) ,
by the distributive law.
Q ) ,
by the distributive law.
 ( P
( P  T ) ,
since ( T
T ) ,
since ( T 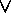 Q )
Q )  T.
T.
 P ,
since ( P
P ,
since ( P
 T )
T )
 P.
P.
Note that by the duality
P
 ( P
( P 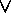 Q )
Q )
 P
also holds.
P
also holds.
More examples of use of identities can be found in the