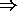 (P
(P  Q).
Q).
To prove that this implication holds, let us first construct a truth table for the proposition P
 Q.
Q.
For example consider the first implication "addition": P 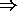 (P
(P  Q).
Q).
To prove that this implication holds, let us first construct
a truth table for the proposition P  Q.
Q.
| P | Q | (P  Q) Q) |
|---|---|---|
| F | F | F |
| F | T | T |
| T | F | T |
| T | T | T |
Then by the definition of 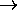 , we
can add a column for P
, we
can add a column for P 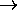 (P
(P  Q)
to obtain the following truth table.
Q)
to obtain the following truth table.
| P | Q | (P  Q) Q) |
P 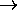 (P (P  Q) Q) |
|---|---|---|---|
| F | F | F | T |
| F | T | T | T |
| T | F | T | T |
| T | T | T | T |
The first row in the rightmost column results since P is false,
and the others in that column follow since (P  Q) is true.
Q) is true.
The rightmost column shows that
P 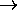 (P
(P  Q)
is always true.
Q)
is always true.
2. Some of the implications can also be proven by using identities and implications
that have already been proven.
For example suppose that
the identity
"exportation":
[(X  Y)
Y)  Z]
Z]
 [X
[X  (Y
(Y  Z)] ,
Z)] ,
and
the implication
"hypothetical syllogism":
[(P  Q)
Q)
 (Q
(Q  R)]
R)]
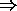 (P
(P  R)
R)
have been proven. Then the implication No. 7:
(P  Q)
Q)
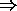 [(Q
[(Q  R)
R)
 (P
(P  R)]
R)]
can be proven by applying the "exportation" to the "hypothetical syllogism" as
follows:
Consider (P  Q) , (Q
Q) , (Q  R) ,
and
(P
R) ,
and
(P  R) in the "hypothetical syllogism" as
X, Y and Z of
the "exportation", respectively.
R) in the "hypothetical syllogism" as
X, Y and Z of
the "exportation", respectively.
Then since [ (X  Y )
Y )
 Z ]
Z ]
 [ X
[ X  ( Y
( Y  Z ) ]
implies [ ( X
Z ) ]
implies [ ( X  Y )
Y )
 Z ]
Z ]
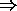 [ X
[ X  ( Y
( Y
 Z ) ] ,
the implication of No. 7 follows.
Z ) ] ,
the implication of No. 7 follows.
Similarly the modus ponens (implication No. 3) can be proven as follows:
Noting that
( P
 Q )
Q )
 (
(  P
P
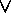 Q ) ,
Q ) ,
P
 ( P
( P
 Q )
Q )
 P
P
 (
(  P
P
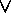 Q )
Q )
 ( P
( P

 P )
P )
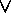 ( P
( P
 Q ) --- by the distributive law
Q ) --- by the distributive law
 F
F
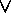 ( P
( P
 Q )
Q )
 ( P
( P
 Q )
Q )
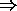 Q
Q
Also the exportation (identity No. 20),
( P  ( Q
( Q  R ) )
R ) )
 ( P
( P  Q )
Q )
 R )
can be proven using identities as follows:
R )
can be proven using identities as follows:
( P  ( Q
( Q  R ) )
R ) )

 P
P
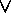 ( Q
( Q  R )
R )

 P
P
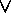 (
(  Q
Q
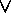 R )
R )
 (
(  P
P
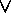
 Q )
Q )
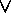 R
R

 ( P
( P
 Q )
Q )
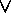 R
R
 ( P
( P
 Q )
Q )
 R
R
3. Some of them can be proven by noting that a proposition in an implication
can be replaced by an equivalent
proposition without affecting its value.
For example by substituting
(  Q
Q 
 P )
for ( P
P )
for ( P  Q ) ,
since they are equivalent being contrapositive to each other, modus tollens
(the implication No. 4):
[ ( P
Q ) ,
since they are equivalent being contrapositive to each other, modus tollens
(the implication No. 4):
[ ( P  Q )
Q ) 
 Q ]
Q ]
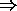
 P ,
reduces to the modus ponens:
[ X
P ,
reduces to the modus ponens:
[ X  ( X
( X  Y ) ]
Y ) ]
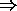 Y.
Hence if the modus ponens and the "contrapositive" in the "Identities" have been proven,
then the modus tollens follows from them.
Y.
Hence if the modus ponens and the "contrapositive" in the "Identities" have been proven,
then the modus tollens follows from them.