Relation
Definition of Binary Relation
Subjects to be Learned
- ordered pair (review)
- equality of ordered pair (review)
- binary relation
- Cartesian product (review)
Contents
Here we are going to define relation formally,
first binary relation,
then general n-ary relation.
A relation in everyday life shows an association of objects of a set with objects of
other sets (or the same set) such as John owns a red Mustang, Jim has a green Miata etc. The essence of
relation is these associations. A collection of these individual associations is a relation,
such as the ownership relation between peoples and automobiles. To represent these individual associations, a set of
"related" objects, such as John and a red Mustang, can be used. However, simple sets such as { John,
a red Mustang } are not sufficient
here.
The order of
the objects must also be taken into account, because John owns a red Mustang but the red Mustang
does not own John, and simple sets do not deal with orders. Thus sets with an order on its members
are needed to describe
a relation.
Here the concept of ordered pair
and, more generally, that of
ordered n-tuple are going to be defined first. A relation is then defined as
a set of ordered pairs or ordered n-tuples.
Definition (ordered pair):
An ordered pair is a set of a pair of objects with an order
associated with them.
If objects are represented by x and y, then we write an ordered pair
as <x, y> or <y, x>. In general <x, y>
is different from <y, x>.
Definition (equality of ordered pairs):
Two ordered pairs <a, b> and <c, d> are
equal
if and only if a = c and b = d.
For example, if the ordered pair <a, b> is equal to <1, 2>,
then a = 1, and b = 2.
<1, 2>
is not equal to the ordered pair <2, 1>.
Definition (binary relation):
A binary relation from a set A to a set
B is a set
of ordered pairs <a, b> where a is an element of A and
b is an element of B.
When an ordered pair <a, b> is in a relation R, we write
a R b, or <a, b>
 R.
It means that element a is related to element b in relation R.
R.
It means that element a is related to element b in relation R.
When A = B, we call a relation from A to B a (binary) relation on A
.
Definition (Cartesian product):
The set of all ordered pairs <a, b>, where a is an element of
A and b is an element of B,
is called the Cartesian product of A and B
and is denoted by A
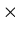 B.
B.
Thus a binary relation from A to B is a subset of Cartesian product
A
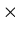 B.
B.
Examples:
If A = {1, 2, 3} and B = {4, 5}, then {<1, 4>,
<2, 5>,
<3, 5>}, for example,
is a binary
relation from A to B.
However,
{<1, 1>, <1, 4>, <3, 5>} is not a binary relation from A to B
because 1 is not in B.
The parent-child relation is a binary relation on the set of people. <John, John Jr.>,
for example, is an element of the parent-child relation if John is the father of John Jr.
Test Your Understanding of Binary Relation
Indicate which of the following statements are correct and which are not.
Click Yes or No , then Submit. There are two sets of questions.
Next -- Definition of Relation (general relation)
Back to Schedule
Back to Table of Contents