Set
Representation of Set
Subjects to be Learned
- representation of set
- list up all the members of set
- describe properties for membership for set
- recursive definition
Contents
A set can be described in a number of different ways.
The simplest is to list up all of its members
if that is possible.
For example {1, 2, 3} is the set of three numbers 1,
2, and
3. { indicates the beginning of the set, and } its end.
Every object between them separated by commas is a member of the set.
Thus {{1, 2}, {{3}, 2}, 2}, {1 } } is
the set of
the elements {1, 2}, {{3}, 2}
and {1}.
A set can also be described by listing the
properties
that its members
must satisfy. For example, { x| 1
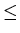 x
x
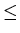 2
and x is a real number. }
represents the set of real numbers between 1 and 2,
and { x| x is the square of an integer and
x
2
and x is a real number. }
represents the set of real numbers between 1 and 2,
and { x| x is the square of an integer and
x
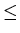 100 } represents the set
{ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 }.
100 } represents the set
{ 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 }.
A third way to describe a set is to give a procedure
to generate the members
of the set. The
recursive/inductive definition is an example and it is going to be studied later.
In this representation, first, basic elements of the set are presented. Then a method
is given to generate elements of the set from known elements of the set.
Thirdly a statement is given that excludes undesirable elements
(which may be included in the set otherwise) from the set.
for example the set of natural numbers N can be defined
recursively as the set that satisfies the following (1), (2), and (3):
(1) 0
 N
N
(2) For any number x
if x  N,
then
x + 1
N,
then
x + 1  N.
N.
(3) Nothing is in N unless it is obtained from (1) and (2).
Following this definition, the set of natural numbers N can be obtained as follows:
First by (1), 0 is put into N.
Then by (2), since 0 is in N, 0 + 1 (= 1)
is in N.
Then by (2) again, 1 + 1 (= 2) is
in N.
Proceeding in this manner all the natural numbers
are put into N.
Note that if we don't have (3), 0.5, 1.5, 2.5, ... can be included in
N, which is not what we want as the set of natural numbers.
Next -- Equality, Subset, etc.
Back to Schedule
Back to Table of Contents