Set
Properties of Set Operation
Subjects to be Learned
- equalities involving set operations
- intersection of sets
- subset relations
- proofs of equalities
- proofs of subset relations
Basic properties of set operations are discussed here. 1 - 6 directly correspond
to
identities
and
implications
of propositional logic, and 7 - 11 also follow immediately from them as illustrated below.
If you widh to review them as well as inference rules
click here.
1.
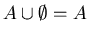
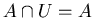
------- Identity Laws
2.
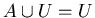
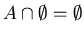
------- Domination Laws
3.
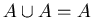
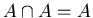
------- Idempotent Laws
4. 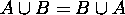
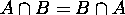
------- Commutative Laws
5. 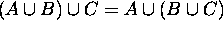
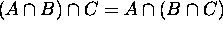
------- Associative Laws
6. 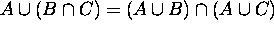
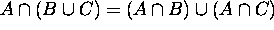
------- Distributive Laws
7. If 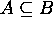 and
and 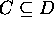 , then
, then 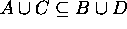 ,
and
,
and 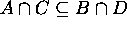 .
.
8. If 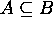 , then
, then 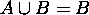 and
and 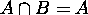 .
.
9. 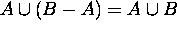
10. 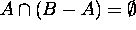
11. 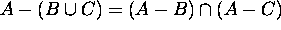 ( cf.
( cf. 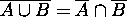 )
)
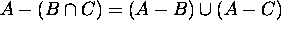 ( cf.
( cf. 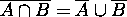 )
)
------- De Morgan's Laws
12. 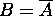 if and only if
if and only if 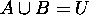 and
and 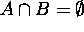
13. 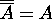 .
.
Additional properties:
14. A
 A
A
 B
B
15. A
 B
B
 A
A
The properties 1 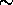 6 , and 11
can be proven using equivalences of propositional logic. The others can also be proven similarly by going to logic,
though they can be proven also using some of these properties (after those properties are proven, needless to say).
Let us prove some of these properties.
6 , and 11
can be proven using equivalences of propositional logic. The others can also be proven similarly by going to logic,
though they can be proven also using some of these properties (after those properties are proven, needless to say).
Let us prove some of these properties.
Proof for 4: 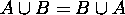
We are going to prove this by showing that every element that is in
A
 B
is also in
B
B
is also in
B
 A
and vice versa.
A
and vice versa.
Consider an arbitrary element x. Then by the definition of set union
x
 A
A
 B
B
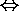 x
x
 A
A
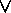 x
x
 B
B
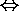 x
x
 A
A
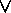 x
x
 B
by the commutativity of
B
by the commutativity of 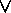
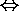 x
x
 B
B
 A
by the definition of set union.
A
by the definition of set union.
Hence by Universal Generalization, every element is in
A
 B
is also in
B
B
is also in
B
 A .
A .
Hence 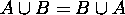 .
.
Note here the correspondence of
the commutativity of
 and that of
and that of
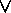 This correspondence holds not just for the commutativity
but also for others.
This correspondence holds not just for the commutativity
but also for others.
Furthermore a similar correspondence exists between
 and
and
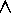 ,
and between
,
and between
 and
and
 .
.
Proof for 6: By the definition of the equality of sets, we need to prove that
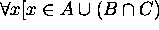 if and only if
if and only if 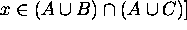
For that, considering the Univesal Generalization rule, we need to show that for an arbitrary element in the universe x,
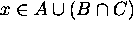 if and only if
if and only if 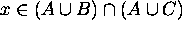
Here the only if part is going to be proven. The if part can be proven similarly.
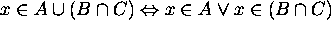 by the definition
of
by the definition
of  .
.
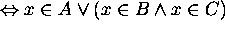 by the definition of
by the definition of  .
.
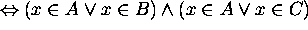 by the distribution
from the equivalences of propositional logic.
by the distribution
from the equivalences of propositional logic.
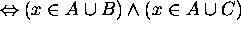 by the definition of
by the definition of  .
.
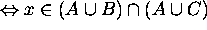 by the definition of
by the definition of  .
.
Proof for 8: (a) If 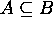 then
then 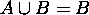 .
.
Let x be an arbitrary element in the universe.
Then 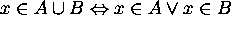 .
.
Since 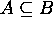 ,
, 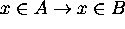 .
.
Also 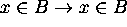 .
.
Hence 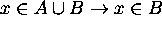 .
.
Hence 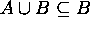 .
.
Since 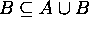 (use "addition" rule),
(use "addition" rule), 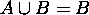 follows.
follows.
(b) Similarly for 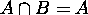 .
.
Alternative proof:
These can also be proven using 8, 14, and 15. For example, (b) can be proven as follows:
First by 15
A
 B
B
 A.
A.
Then since
A
 A, and
A
A, and
A
 B, by 7
A
B, by 7
A
 A
A
 A
A
 B .
B .
Since A
 A
= A by 3,
A
A
= A by 3,
A
 A
A
 B .
B .
Proof for 9: Let x be an arbitrary element in the universe.
Then 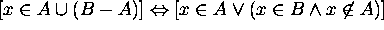
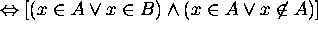
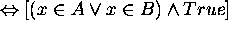
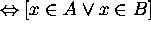
Hence 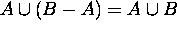 .
.
Alternative proof
This can also proven using set properties as follows.
A
 ( B - A )
= A
( B - A )
= A
 ( B
( B

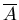 ) by the definition of ( B - A ) .
) by the definition of ( B - A ) .
= ( A
 B )
B )
 ( A
( A

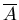 ) by the distribution.
) by the distribution.
= ( A
 B )
B )
 U
U
= ( A
 B )
by 1.
B )
by 1.
Proof for 10: Suppose 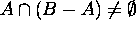 .
.
Then there is an element x that is in 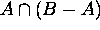 , i.e.
, i.e.
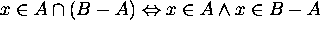
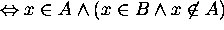
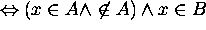
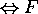
Hence 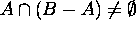 does not hold.
does not hold.
Hence 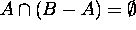 .
.
This can also be proven in the similar manner to 9 above.
Proof for 11: Let x be an arbitrary element in the universe.
Then 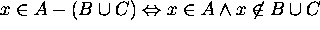
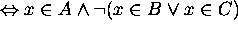
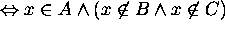
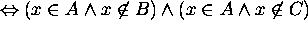
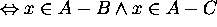
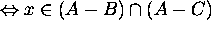
Hence 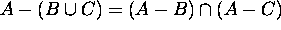
Proof for 12: (a) 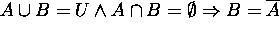 ?
?
Try to prove 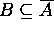 and
and 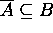 .
.
Let x be an arbitrary element in the universe.
Then if 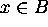 , then
, then 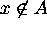 since
since 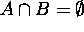 . Hence
. Hence 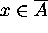 .
.
Hence 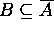 .
.
If 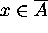 , then
, then 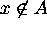 . Since
. Since 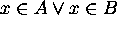 (from
(from 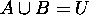 ),
),
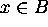 must hold. Hence
must hold. Hence 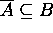 .
.
Hence 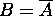 .
.
(b) 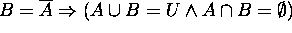 ?
?
Since 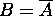 ,
, 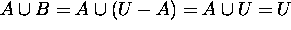 since
since 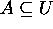 .
.
Also 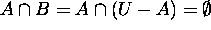 by 10 above.
by 10 above.
Proof for 13: Since 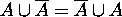 ,
, 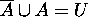 .
.
Also since 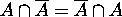 ,
, 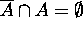 .
.
Hence A satisfies the conditions for the complement of 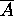 .
.
Hence 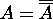 .
.
Next -- Recursive Definition
Back to Schedule
Back to Table of Contents
 B
B
 B
B
 and
and