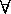 x x > 1".
This new statement is true or false in the universe of discourse. Hence it is a proposition.
x x > 1".
This new statement is true or false in the universe of discourse. Hence it is a proposition.
Quantification --- Forming Propositions from Predicates
A predicate with variables is not a proposition. For example,
the statement x > 1 with variable x over the universe of real numbers
is neither true nor false since we don't know what x is. It can be true
or false depending on the value of x.
For x > 1 to be a proposition either we substitute a specific number for x
or change it to something like "There is a number x for which x > 1 holds",
or "For every number x, x > 1 holds".
More generally, a predicate with variables (
For example, x > 1 becomes 3 > 1 if 3 is assigned to x, and it becomes a true statement, hence a proposition.
In general, a quantification is performed on formulas of predicate logic
(called
The universal quantifier turns, for example, the statement x > 1
to "for every object x
in the universe, x > 1", which is expressed as "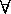 x x > 1".
This new statement is true or false in the universe of discourse. Hence it is a proposition.
x x > 1".
This new statement is true or false in the universe of discourse. Hence it is a proposition.
Similarly the existential quantifier turns, for example, the statement x > 1
to "for some
object x in the universe, x > 1", which is expressed as " x x > 1." Again, it is true or false in the universe of discourse, and hence
it is a proposition.
x x > 1." Again, it is true or false in the universe of discourse, and hence
it is a proposition.
The Universal Quantifier
The expression:
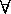 x P(x), denotes the universal quantification
of the atomic formula P(x). Translated into the English language, the expression is understood as:
"For all x, P(x) holds" or "for every x, P(x) holds".
x P(x), denotes the universal quantification
of the atomic formula P(x). Translated into the English language, the expression is understood as:
"For all x, P(x) holds" or "for every x, P(x) holds".
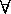 is called the universal quantifier,
and
is called the universal quantifier,
and
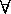 x means all the objects x in the universe. If this is
followed by P(x) then the meaning is that P(x) is true for every object
x in the universe. For
example, "All cars have wheels" could be transformed into the propositional form,
x means all the objects x in the universe. If this is
followed by P(x) then the meaning is that P(x) is true for every object
x in the universe. For
example, "All cars have wheels" could be transformed into the propositional form,
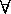 x P(x), where:
x P(x), where:
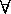 x P(x) is equivalent to the conjunction:
P(x1))
x P(x) is equivalent to the conjunction:
P(x1)) 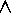 P(x2)
P(x2)
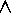 P(x3)
P(x3)
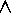 ...
... 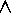 P(xn) .
P(xn) .
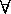 x P(x),
if we knew that there were only 4 cars in our universe of discourse (c1, c2, c3 and
c4) then we could also translate the statement as:
P(c1)
x P(x),
if we knew that there were only 4 cars in our universe of discourse (c1, c2, c3 and
c4) then we could also translate the statement as:
P(c1) 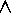 P(c2)
P(c2) 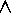 P(c3)
P(c3)
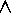 P(c4)
P(c4)
The Existential Quantifier
The expression:
 xP(x), denotes the existential
quantification of P(x). Translated into the English language, the expression could also be understood as:
"There exists an x such that P(x)"
or
"There is at least one x such that P(x)"
xP(x), denotes the existential
quantification of P(x). Translated into the English language, the expression could also be understood as:
"There exists an x such that P(x)"
or
"There is at least one x such that P(x)"
 is called the existential quantifier,
and
is called the existential quantifier,
and
 x means at least one object x in the universe. If this is
followed by P(x) then the meaning is that P(x) is true for at least one object
x of the universe.
For example, "Someone loves you" could be transformed into the propositional form,
x means at least one object x in the universe. If this is
followed by P(x) then the meaning is that P(x) is true for at least one object
x of the universe.
For example, "Someone loves you" could be transformed into the propositional form,
 x P(x), where:
x P(x), where:
Existential Quantifier and Connective OR
If all the elements in the universe of discourse can be listed, then the existential quantification
 xP(x) is equivalent to the disjunction:
P(x1)
xP(x) is equivalent to the disjunction:
P(x1) 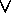 P(x2)
P(x2) 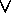 P(x3)
P(x3)
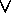 ...
... 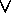 P(xn).
P(xn).
For example, in the above example of  x P(x),
if we knew that there were only 5 living creatures in our universe of discourse
(say: me, he, she, rex and fluff), then we could also write the statement as:
P(me)
x P(x),
if we knew that there were only 5 living creatures in our universe of discourse
(say: me, he, she, rex and fluff), then we could also write the statement as:
P(me) 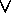 P(he)
P(he) 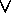 P(she)
P(she)
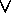 P(rex)
P(rex) 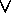 P(fluff)
P(fluff)
An appearance of a variable in a
For example,
in  x P(x, y), the variable x
is bound while y is free.
In
x P(x, y), the variable x
is bound while y is free.
In 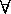 x [
x [  y
P(x, y)
y
P(x, y) 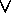 Q(x, y) ] , x and the y in P(x, y)
are bound, while y in Q(x, y) is free, because the scope of
Q(x, y) ] , x and the y in P(x, y)
are bound, while y in Q(x, y) is free, because the scope of
 y is P(x, y).
The scope of
y is P(x, y).
The scope of
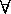 x is [
x is [  y
P(x, y)
y
P(x, y) 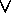 Q(x, y) ] .
Q(x, y) ] .
Order of Application of Quantifiers
When more than one variables are quantified in a wff such as
 y
y 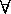 x
P( x, y ), they are applied from the inside, that is, the one closest to
the atomic formula is applied first. Thus
x
P( x, y ), they are applied from the inside, that is, the one closest to
the atomic formula is applied first. Thus
 y
y 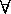 x
P( x, y )
reads
x
P( x, y )
reads  y [
y [ 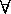 x
P( x, y ) ] ,
and we say for some y, P( x, y ) holds
for every x.
x
P( x, y ) ] ,
and we say for some y, P( x, y ) holds
for every x.
The positions of the same type of quantifiers can be switched
without affecting the truth value
as long as there are
no
quantifiers of the other type between the ones to be interchanged.
For example
 x
x  y
y
 z P(x, y , z)
is equivalent to
z P(x, y , z)
is equivalent to
 y
y  x
x
 z P(x, y , z),
z P(x, y , z),
 z
z  y
y
 x P(x, y , z),
etc.
It is the same for the universal quantifier.
x P(x, y , z),
etc.
It is the same for the universal quantifier.
However, the positions of different types of quantifiers can
not be switched.
For example
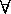 x
x  y
P( x, y ) is not equivalent to
y
P( x, y ) is not equivalent to
 y
y 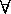 x
P( x, y ). For let P( x, y ) represent x
< y for the set of numbers as the universe, for example. Then
x
P( x, y ). For let P( x, y ) represent x
< y for the set of numbers as the universe, for example. Then x
 y
P( x, y ) reads "for every number x, there is a number
y that is greater than x", which is true, while
y
P( x, y ) reads "for every number x, there is a number
y that is greater than x", which is true, while y
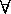 x
P( x, y ) reads "there is a number y that is
greater than
any number",
which is not true.
x
P( x, y ) reads "there is a number y that is
greater than
any number",
which is not true.