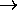 Q, the proposition
Q
Q, the proposition
Q 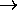 P is called its converse,
and the proposition
P is called its converse,
and the proposition  Q
Q 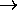
 P is called its contrapositive.
P is called its contrapositive.
For example for the proposition "If it rains, then I get wet",
Converse: If I get wet, then it rains.
Contrapositive: If I don't get wet, then it does not rain.
The converse of a proposition is not necessarily logically equivalent to it, that is
they may or may not take the same truth value at the same time.
On the other hand, the contrapositive of a proposition is always
logically equivalent to the proposition. That is, they take the same truth value regardless
of the values of their constituent variables.
Therefore, "If it rains, then I get wet." and "If I don't get wet,
then it does not rain." are logically equivalent. If one is true then the other is also true, and vice versa.