What is a set?
        Set is a group of elements, having a property that characterizes those elements.

        How to specify a Set?
        One way is to enumerate the elements completely. All the elements belonging to the set are explicitly given.

                Example:   A = {1,2,3,4,5}

         Alternate way is to give the properties that characterize the elements of the set.

                Example: B = {x | x is a positive integer less than or equal to 5}

        Some sets can also be defined recursively.
 

       Set terminology

        Belongs To
            x  B  means that  x  is an element of set B. Using this notation we can specify the set {0,1,2,3,4} call it Z
            by writing

                     Z = {x | x 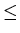 N | x 5}
            where N represents the set of natural numbers.
            It is read as "the set of natural numbers that are less than or equal to 5".
 

       Subset
            Let A and B be two sets.

            A is a subset of B, if every element of A is an element of B.

            A is a subset of B is represented as A  B.

            Note:  If A is a subset of B and B is a subset of A then A=B. Also, if A is a subset of, but not equal to B
                        represented as A 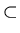 B.

        Universal Set
            The set U of all the elements we might ever consider in the discourse is called the universal set.

        Complement
            If A is a set, then the complement of A is the set consisting of all elements of the universal set
            that are not in A. It is denoted by A' or . Thus
            A' = { x | x U ^ x  A } ,   where     means " is not an element of "..
            Example:
                 If U is the set of natural numbers and A = { 1,2,3 } , then A' = { x | x U ^ x > 3 } .
 

       Set Operations

            The operations that can be performed on sets are:

           1. Union
                   If A and B are two sets, then the union of A and B is the set that contains all the elements that are in
                   A and B including the ones in both A and B. It is denoted by A  B.

                   Example:  If   A = {1,2,3} and B = {3,4,5}
                                   then A  B = {1,2,3,4,5}

            2. Difference
                    If A and B are two sets, then the difference of A from B is the set that consists of the elements of A
                    that are not in B. It is denoted by A - B.

                    Example:  If A = {1,2,3} B = {3,4,5}
                                    then A - B = {1,2}

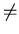                    Note that in general A - B B - A .
                    For A and B of the above example B - A = {4,5} .

            3. Intersection
                    If A and B are two sets, then the intersection of A and B is the set that consists of the elements in
                    both A and B . It is denoted by A  B.
                    Example:  If A = {1,2,3,8}     B = {3,4,5,8}
                                    then A B = {3,8}.

        Disjoint sets
             A and B are said to be disjoint if they contain no elements in common
             i.e. A  B =  ø, where ø  is the Empty set.

             Example:   A = { 1,2,3,4,5 }    and     B = { 6,8,9 } are disjoint.

        Following is a list of some standard Set Identities
         A, B, C represent arbitrary sets and ø is the empty set and U is the Universal Set.

    The Commutative laws:
             A  B = B  A
             A  B = B  A

    The Associative laws:
             A  (B  C) = (A  B)  C
             A  (B  C) = (A  B)  C

    The Distributive laws:
             A  (B  C) = (A  B)  (A  C)
             A  (B  C) = (A  B)  (A  C)

    The Idempotent laws:
             A  A = A
             A A = A

    The Absorptive laws:
             A  (A  B) = A
             A  (A  B) = A

    The De Morgan laws:
             (A  B)' = A' B'
             (A  B)' = A' B'

    Other laws involving Complements:
             ( A' )' = A
             A  A' = ø
             A  A' = U

    Other laws involving the empty set
             A  ø = A
             A  ø = ø

    Other laws involving the Universal Set:
             A  U = U
             A  U = A

    Venn Diagrams
    A common technique in working with Set Operations is to illustrate them by drawing Venn Diagrams.
    It is a very good tool to get a general idea.
    Note, however, that Venn Diagrams must NOT be used for rigorous discussions, because they can represent
    only very limited situations and miss many other possibilities.

    The idea of Venn Diagram is to draw a region representing the universe and within that to draw the regions
    representing the component sets we are starting with so that the resulting diagram describes their
    interrelationships.

   For example sets A = { 1,2,3,4 }  and   B = { 6,8,2,4 } can be represented as shown below using Venn Diagrams:

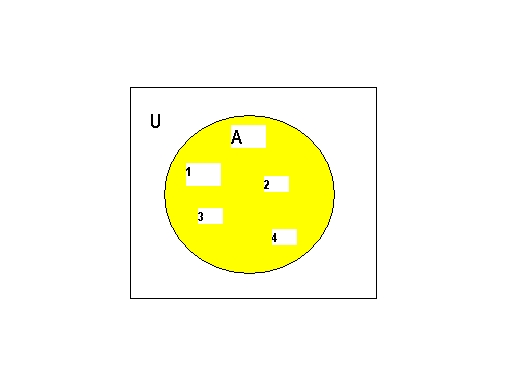
                                                       Set A


U represents the Universal set in which  A is one of the Set.
 

     
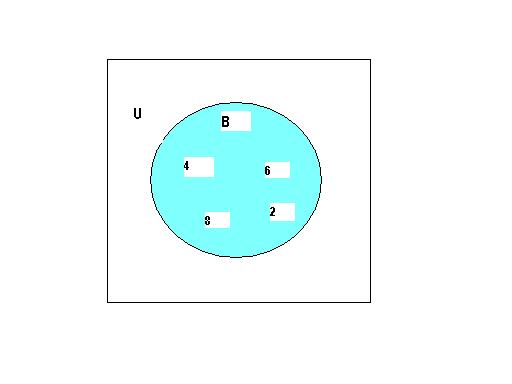
                                               Set B

The following Venn Diagram is used to illustrate A  B

                                     A  B
 

The following Venn Diagram is used to illustrate A U B

                                     A  B


    A  B is the set consisting of all the different elements in A and B.
 
 

    (A  B)' is the yellow region in the Venn diagram given below.

      For example:     U = { 1,2,3,4,5,6,7,8 }    A = { 1,2,3,4 }     B = { 2,4,6,8 }
                               A  B = { 1,2,3,4,6,8 }
                               (A  B)' =  U - (A  B)
                                              = { 5, 7 }
 

    A - B  is the yellow shaded region and
    B - A is the blue shaded region in the Venn Diagram shown below

        Generalized Set Operations

        Union, intersection and Cartesian product of sets are associative.

        For example   holds. To denote either of these expressions
        we often use A B C .

        This can be generalized for the union of any finite number of sets as A₁ A₂ .... A_n ,

        which we write as

           A_i

        This generalized union of sets can be rigorously defined as follows:

        Definition ( A_i) :

        Basis Clause: For n = 1 ,   A_i = A₁.

        Inductive Clause:   A_i = ( A_i) A_n+1

        Similarly the generalized intersection A_i and generalized Cartesian product A_i can be defined.

        Based on these definitions, De Morgan's law on set union and intersection can also be generalized as follows:

        Theorem (Generalized De Morgan)

             = ,     and

             =

        Proof: These can be proven by induction on n and are left as an exercise.