Finite Automata
Proof of Equivalence of NFA- and NFA
and NFA
We are going to prove that the NFA obtained from
NFA- by the conversion algorithm
accepts the same language as the NFA-
by the conversion algorithm
accepts the same language as the NFA- .
.
NFA- that recognizes a language L is denoted by
M1 = < Q1 ,
that recognizes a language L is denoted by
M1 = < Q1 ,  , q1,0 ,
, q1,0 ,
 1 , A1 > and
NFA obtained by the conversion is denoted by M2 = < Q2,
1 , A1 > and
NFA obtained by the conversion is denoted by M2 = < Q2,
 ,
q2,0 ,
,
q2,0 ,  2 , A2 >
2 , A2 >
First we are going to prove that
 1*( q , w ) =
1*( q , w ) =
 2*( q , w )
for any non-empty string w.
2*( q , w )
for any non-empty string w.
To review the definition of  *
for NFA,
and NFA-
*
for NFA,
and NFA- ,
and the conversion of
NFA-
,
and the conversion of
NFA- to NFA
click here.
to NFA
click here.
When it is proven, it implies that
NFA- M1 and NFA M2
accept the same non-empty strings.
The case when w is an empty string is going to be proven separately.
M1 and NFA M2
accept the same non-empty strings.
The case when w is an empty string is going to be proven separately.
Claim 1: For any non-empty string w and for any state q,
 1*( q , w ) =
1*( q , w ) =
 2*( q , w ) .
2*( q , w ) .
Proof: This is going to be proven by induction on w.
Recall that the set of strings is defined recursively
(click here for a quick review). Thus we first prove that it is true
for any arbitrary symbol, then assuming it holds for any arbitrary string w we prove it
for any of the children of w, that is wa for any symbol a in the alphabet.
Basis Step: We need to show that for any symbol a in 
 1*( q , a ) =
1*( q , a ) =
 2*( q , a ) .
2*( q , a ) .
We are going to prove it by showing that both of them are equal to
 2( q , a ) .
2( q , a ) .
Firstly  2( q , a ) =
2( q , a ) =
 1*( q , a ) --- (1)
1*( q , a ) --- (1)
because of the way NFA
is constructed from NFA- (click here for a review)
.
(click here for a review)
.
Secondly
 2*( q , a ) =
2*( q , a ) =
 2*(q ,
2*(q ,  a )
=
a )
= 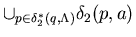
by the definition of  2* for NFA
(click here for a review)
.
.
2* for NFA
(click here for a review)
.
.
Since  2*(q ,
2*(q ,  )
= { q } ,
)
= { q } ,
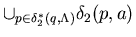 =
= 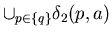 =
=  2( q , a ) .
2( q , a ) .
Hence
 2*( q , a ) =
2*( q , a ) =
 2( q , a ) . --- (2)
2( q , a ) . --- (2)
Hence from (1) and (2),
 1*( q , a ) =
1*( q , a ) =
 2*( q , a ) .
2*( q , a ) .
Inductive Step: We need to show that if
 1*( q , w ) =
1*( q , w ) =
 2*( q , w )
for an arbitrary string w (Induction Hypothesis),
2*( q , w )
for an arbitrary string w (Induction Hypothesis),
then
 1*( q , wa ) =
1*( q , wa ) =
 2*( q , wa ) holds
for any arbitrary symbol a in
2*( q , wa ) holds
for any arbitrary symbol a in  .
.
First we show that
 2*( q , wa ) =
2*( q , wa ) =
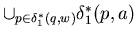 --- (1)
--- (1)
using the definition of  2*,
the induction hypothesis and the construction of NFA from NFA-
2*,
the induction hypothesis and the construction of NFA from NFA- .
.
Then we show that 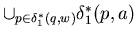 =
=  1*( q , wa ) --- (2)
1*( q , wa ) --- (2)
basically using the definition of  1*.
1*.
Then from (1) and (2) we can see that
 1*( q , wa ) =
1*( q , wa ) =
 2*( q , wa ) .
2*( q , wa ) .
Let us first prove (1).
By the definition of  2*
2*
 2*( q , wa ) =
2*( q , wa ) =
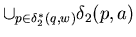
Since  2*( q , w ) =
2*( q , w ) =
 1*( q , w )
by the induction hypothesis,
1*( q , w )
by the induction hypothesis,
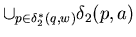 =
=
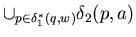
Since  2( q , a ) =
2( q , a ) =
 1*( q , a ) by the way NFA
is constructed from NFA-
1*( q , a ) by the way NFA
is constructed from NFA- .
.
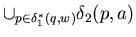 =
=
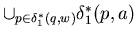
Hence
 2*( q , wa ) =
2*( q , wa ) =
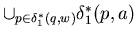 , that is (1) has been proven.
, that is (1) has been proven.
Let us next prove (2), that is
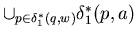 =
=  1*( q , wa ) .
1*( q , wa ) .
By the definition of  1* for
NFA-
1* for
NFA- ,
,
 1*( p , a ) =
1*( p , a ) =
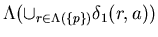
Substituting this into the left hand side of (2) produces
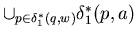 =
=
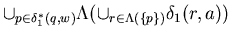 .
.
The right hand side of this equality is equal to
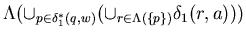 ( the first
( the first  and
and  have been swapped to get this) ,
have been swapped to get this) ,
as proven below in Claim 3,
This can be shown to be equal to 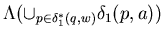 ,
because
,
because
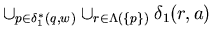 =
= 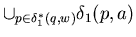 .
.
To see an explanation for this
click here.
Hence 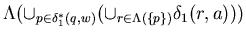 =
= 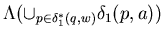 .
.
On the other hand
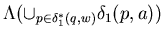 =
=
 1*( q , wa ) ,
by the definition of
1*( q , wa ) ,
by the definition of  1* .
1* .
Hence
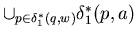 =
=  1*( q , wa ) .
1*( q , wa ) .
Hence we have proven (2).
Thus from (1) and (2)
 1*( q , wa ) =
1*( q , wa ) =
 2*( q , wa ) .
2*( q , wa ) .
End of Induction
With this Claim 1 we can see that any non-empty string w is accepted by NFA
if and only if it is accepted by the corresponding
NFA- .
.
As for the empty string  , if it is accepted
by an NFA-
, if it is accepted
by an NFA- , then
, then
 ( { q10 } )
( { q10 } ) 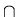 A1
A1 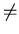
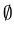 .
Hence by the way A2 is constructed, q20
.
Hence by the way A2 is constructed, q20
 A2 .
Hence
A2 .
Hence  is accepted by NFA.
is accepted by NFA.
Conversely if  is accepted by NFA, then
q20
is accepted by NFA, then
q20
 A2 .
By the way NFA is constructed from NFA-
A2 .
By the way NFA is constructed from NFA- this means that
this means that
 ( { q10 } )
( { q10 } ) 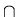 A1
A1 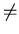
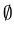 .
Hence
.
Hence  is accepted by
NFA-
is accepted by
NFA- .
.
Thus NFA- and the corresponding NFA
accept the same language.
and the corresponding NFA
accept the same language.
As a preparation for the proof of commutativity of union and
 -closure
operations, let us prove the following claim.
-closure
operations, let us prove the following claim.
Claim 2:  ( S
( S  T )
=
T )
=  ( S )
( S ) 
 ( T ) .
( T ) .
We are going to prove this in two parts:
 ( S
( S  T )
T )

 ( S )
( S ) 
 ( T ) and
( T ) and
 ( S )
( S ) 
 ( T )
( T )

 ( S
( S  T ) .
T ) .
Part 1 :
 ( S
( S  T )
T )

 ( S )
( S ) 
 ( T )
( T )
This is going to be proven by induction on
 ( S
( S  T ) .
T ) .
For that let us restate the statement so that the induction becomes clearer.
What Part 1 states is that all the elements of
 ( S
( S  T )
have the property of being in the set
T )
have the property of being in the set
 ( S )
( S ) 
 ( T ) .
( T ) .
Since  ( S
( S  T )
is defined recursively, in the Basis Step of our proof we prove the property
for the elements of the basis of
T )
is defined recursively, in the Basis Step of our proof we prove the property
for the elements of the basis of
 ( S
( S  T )
and in the Inductive Step we prove that if an arbitrary element of
T )
and in the Inductive Step we prove that if an arbitrary element of
 ( S
( S  T ) has
that property, then its childen also have it.
T ) has
that property, then its childen also have it.
Let us review the definition of the  -closure of
the set of states of an NFA-
-closure of
the set of states of an NFA- .
Let X be the set of states of an NFA-
.
Let X be the set of states of an NFA- . Then the
. Then the
 -closure of X is defined recursively as
-closure of X is defined recursively as
Basis Clause: X 
 ( X ) .
( X ) .
Inductive Clause: If q 
 ( X ) , then
( X ) , then
 ( q ,
( q ,  )
)

 ( X ) .
( X ) .
Extremal Clause: Nothng is in  ( X ) unless it is
obtained by the Basis and Inductive Clauses.
( X ) unless it is
obtained by the Basis and Inductive Clauses.
Proof of Part 1:
Basis Step: We need to prove that ( S  T )
T )

 ( S )
( S ) 
 ( T ) .
( T ) .
Since S 
 ( S )
and T
( S )
and T 
 ( T ) ,
S and T are subsets of
( T ) ,
S and T are subsets of
 ( S )
( S ) 
 ( T ) .
Hence
( S
( T ) .
Hence
( S  T )
T )

 ( S )
( S ) 
 ( T ) .
( T ) .
Inductive Step: We need to prove that if q is an
arbitrary element of
 ( S
( S  T )
with the property of being in
T )
with the property of being in  ( S )
( S )

 ( T ) ,
then
( T ) ,
then
 ( q ,
( q ,
 )
)

 ( S )
( S ) 
 ( T ) .
( T ) .
Let q be an
arbitrary element of
 ( S
( S  T )
with the property of being in
T )
with the property of being in  ( S )
( S )

 ( T ) .
( T ) .
Since q 
 ( S )
( S ) 
 ( T ) ,
q
( T ) ,
q 
 ( S ) or
q
( S ) or
q 
 ( T ) .
( T ) .
If q 
 ( S ) , then
( S ) , then
 ( q ,
( q ,
 )
)

 ( S ) by the definition of
( S ) by the definition of
 ( S ) . Hence
( S ) . Hence
 ( q ,
( q ,
 )
)

 ( S )
( S )

 ( T ) .
( T ) .
Similarly if q 
 ( T ) , then
( T ) , then
 ( q ,
( q ,
 )
)

 ( S )
( S )

 ( T ) .
( T ) .
Hence
if q is an
arbitrary element of
 ( S
( S  T )
with the property of being in
T )
with the property of being in  ( S )
( S )

 ( T ) ,
then
( T ) ,
then
 ( q ,
( q ,
 )
)

 ( S )
( S ) 
 ( T ) .
( T ) .
Thus all the elements of
 ( S
( S  T )
have the property of being in
T )
have the property of being in
 ( S )
( S ) 
 ( T ) which is to say that
( T ) which is to say that
 ( S
( S  T )
T )

 ( S )
( S ) 
 ( T ) .
( T ) .
End of Proof for Part 1
Part 2 :
 ( S )
( S ) 
 ( T )
( T )

 ( S
( S  T ) .
T ) .
Proof of Part 2: We are going to prove
 ( S )
( S )

 ( S
( S  T ) and
T ) and
 ( T )
( T )

 ( S
( S  T ) .
That would imply that
T ) .
That would imply that
 ( S )
( S ) 
 ( T )
( T )

 ( S
( S  T ) .
T ) .
Proof of  ( S )
( S )

 ( S
( S  T ) :
T ) :
By induction on  ( S ) .
( S ) .
Basis Step: We need to show that S 
 ( S
( S  T ) .
T ) .
Since S  ( S
( S  T ) , and
( S
T ) , and
( S  T )
T )

 ( S
( S  T ) ,
S
T ) ,
S 
 ( S
( S  T ) .
T ) .
Inductive Step: We need to prove that for an arbitrary element q in
 ( S ) , if q is in
( S ) , if q is in
 ( S
( S  T ) ,
then
T ) ,
then  ( q ,
( q ,
 )
)

 ( S
( S  T ) .
T ) .
Since q is in
 ( S
( S  T )
and since
T )
and since  ( S
( S  T )
is a
T )
is a  -closure, by the definition of
-closure, by the definition of
 -closure
-closure  ( q ,
( q ,
 )
)

 ( S
( S  T ) .
T ) .
Thus  ( S )
( S )

 ( S
( S  T )
has been proven.
T )
has been proven.
Similarly  ( T )
( T )

 ( S
( S  T ) holds.
T ) holds.
Hence  ( S )
( S ) 
 ( T )
( T )

 ( S
( S  T ) holds.
T ) holds.
End of Proof of Part 2
End of Proof of Claim 2
Claim 3:  (
(
 Si ) =
Si ) =

 ( Si ) .
( Si ) .
Proof : Proof by induction on n.
Basis Step: n = 1. If n = 1, then  (
(
 Si )
=
Si )
=  ( S1 ) and
( S1 ) and

 ( Si )
=
( Si )
=  ( S1 ) .
( S1 ) .
Hence  (
(
 Si ) =
Si ) =

 ( Si )
holds for n = 1.
( Si )
holds for n = 1.
Inductive Step: Assume that  (
(
 Si ) =
Si ) =

 ( Si )
holds for n. --- Inducion Hypothesis
( Si )
holds for n. --- Inducion Hypothesis
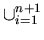
 ( Si )
= (
( Si )
= ( 
 ( Si ) )
( Si ) )

 ( Sn+1 )
by the definition of union.
( Sn+1 )
by the definition of union.
=  (
(  Si )
Si )

 ( Sn+1 )
by the induction hypothesis.
( Sn+1 )
by the induction hypothesis.
=  ( (
( (  Si )
Si )
 Sn+1 ) by Claim 2 above, since
Sn+1 ) by Claim 2 above, since  Si is a set as well as Sn+1.
Si is a set as well as Sn+1.
=  (
( 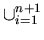 Si )
by the definition of union.
Si )
by the definition of union.
End of Proof for Claim 3
Test Your Understanding of Proof of Equivalence of NFA and NFA-
Indicate which of the following statements are correct and which are not.
Click Yes or No , then Submit.
There are two sets of questions.
The following notations are used in the questions:
 : \delta
: \delta
 : \Lambda
: \Lambda
 : \Sigma
: \Sigma
 * : \Sigma^*
* : \Sigma^*
 : \cup
: \cup
Next -- Kleene's Theorem --- Part 1
Back to Study Schedule
Back to Table of Contents
 and NFA
and NFA by the conversion algorithm
accepts the same language as the NFA-
by the conversion algorithm
accepts the same language as the NFA- .
.
 that recognizes a language L is denoted by
M1 = < Q1 ,
that recognizes a language L is denoted by
M1 = < Q1 ,  , q1,0 ,
, q1,0 ,
 1 , A1 > and
NFA obtained by the conversion is denoted by M2 = < Q2,
1 , A1 > and
NFA obtained by the conversion is denoted by M2 = < Q2,
 ,
q2,0 ,
,
q2,0 ,  2 , A2 >
2 , A2 >
 1*( q , w ) =
1*( q , w ) =
 2*( q , w )
for any non-empty string w.
2*( q , w )
for any non-empty string w.
 *
for NFA,
and NFA-
*
for NFA,
and NFA- ,
and the conversion of
NFA-
,
and the conversion of
NFA- to NFA
click here.
to NFA
click here.
 M1 and NFA M2
accept the same non-empty strings.
The case when w is an empty string is going to be proven separately.
M1 and NFA M2
accept the same non-empty strings.
The case when w is an empty string is going to be proven separately.
 1*( q , w ) =
1*( q , w ) =
 2*( q , w ) .
2*( q , w ) .

 1*( q , a ) =
1*( q , a ) =
 2*( q , a ) .
2*( q , a ) .
 2( q , a ) .
2( q , a ) .
 2( q , a ) =
2( q , a ) =
 1*( q , a ) --- (1)
1*( q , a ) --- (1)
 (click here for a review)
.
(click here for a review)
.
 2*( q , a ) =
2*( q , a ) =
 2*(q ,
2*(q ,  a )
=
a )
= 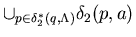
 2* for NFA
(click here for a review)
.
.
2* for NFA
(click here for a review)
.
.
 2*(q ,
2*(q ,  )
= { q } ,
)
= { q } ,
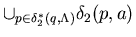 =
= 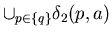 =
=  2( q , a ) .
2( q , a ) .
 2*( q , a ) =
2*( q , a ) =
 2( q , a ) . --- (2)
2( q , a ) . --- (2)
 1*( q , a ) =
1*( q , a ) =
 2*( q , a ) .
2*( q , a ) .
 1*( q , w ) =
1*( q , w ) =
 2*( q , w )
for an arbitrary string w (Induction Hypothesis),
2*( q , w )
for an arbitrary string w (Induction Hypothesis),
 1*( q , wa ) =
1*( q , wa ) =
 2*( q , wa ) holds
for any arbitrary symbol a in
2*( q , wa ) holds
for any arbitrary symbol a in  .
.
 2*( q , wa ) =
2*( q , wa ) =
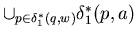 --- (1)
--- (1)
 2*,
the induction hypothesis and the construction of NFA from NFA-
2*,
the induction hypothesis and the construction of NFA from NFA- .
.
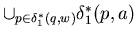 =
=  1*( q , wa ) --- (2)
1*( q , wa ) --- (2)
 1*.
1*.
 1*( q , wa ) =
1*( q , wa ) =
 2*( q , wa ) .
2*( q , wa ) .
 2*
2*
 2*( q , wa ) =
2*( q , wa ) =
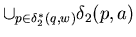
 2*( q , w ) =
2*( q , w ) =
 1*( q , w )
by the induction hypothesis,
1*( q , w )
by the induction hypothesis,
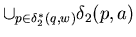 =
=
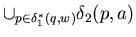
 2( q , a ) =
2( q , a ) =
 1*( q , a ) by the way NFA
is constructed from NFA-
1*( q , a ) by the way NFA
is constructed from NFA- .
.
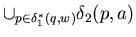 =
=
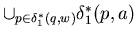
 2*( q , wa ) =
2*( q , wa ) =
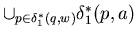 , that is (1) has been proven.
, that is (1) has been proven.
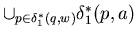 =
=  1*( q , wa ) .
1*( q , wa ) .
 1* for
NFA-
1* for
NFA- ,
,
 1*( p , a ) =
1*( p , a ) =
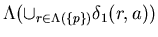
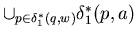 =
=
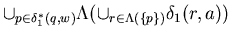 .
.
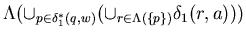 ( the first
( the first  and
and  have been swapped to get this) ,
have been swapped to get this) ,
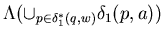 ,
because
,
because
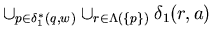 =
= 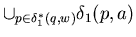 .
.
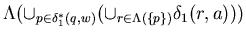 =
= 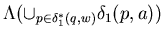 .
.
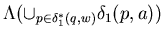 =
=
 1*( q , wa ) ,
by the definition of
1*( q , wa ) ,
by the definition of  1* .
1* .
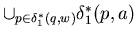 =
=  1*( q , wa ) .
1*( q , wa ) .
 1*( q , wa ) =
1*( q , wa ) =
 2*( q , wa ) .
2*( q , wa ) .
 .
.
 , if it is accepted
by an NFA-
, if it is accepted
by an NFA- , then
, then
 ( { q10 } )
( { q10 } ) 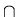 A1
A1 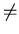
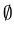 .
Hence by the way A2 is constructed, q20
.
Hence by the way A2 is constructed, q20
 A2 .
Hence
A2 .
Hence  is accepted by NFA.
is accepted by NFA.
 is accepted by NFA, then
q20
is accepted by NFA, then
q20
 A2 .
By the way NFA is constructed from NFA-
A2 .
By the way NFA is constructed from NFA- this means that
this means that
 ( { q10 } )
( { q10 } ) 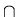 A1
A1 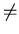
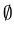 .
Hence
.
Hence  is accepted by
NFA-
is accepted by
NFA- .
.
 and the corresponding NFA
accept the same language.
and the corresponding NFA
accept the same language.
 -closure
operations, let us prove the following claim.
-closure
operations, let us prove the following claim.
 ( S
( S  T )
=
T )
=  ( S )
( S ) 
 ( T ) .
( T ) .
 ( S
( S  T )
T )

 ( S )
( S ) 
 ( T ) and
( T ) and
 ( S )
( S ) 
 ( T )
( T )

 ( S
( S  T ) .
T ) .
 ( S
( S  T )
T )

 ( S )
( S ) 
 ( T )
( T )
 ( S
( S  T ) .
T ) .
 ( S
( S  T )
have the property of being in the set
T )
have the property of being in the set
 ( S )
( S ) 
 ( T ) .
( T ) .
 ( S
( S  T )
is defined recursively, in the Basis Step of our proof we prove the property
for the elements of the basis of
T )
is defined recursively, in the Basis Step of our proof we prove the property
for the elements of the basis of
 ( S
( S  T )
and in the Inductive Step we prove that if an arbitrary element of
T )
and in the Inductive Step we prove that if an arbitrary element of
 ( S
( S  T ) has
that property, then its childen also have it.
T ) has
that property, then its childen also have it.
 -closure of
the set of states of an NFA-
-closure of
the set of states of an NFA- .
Let X be the set of states of an NFA-
.
Let X be the set of states of an NFA- . Then the
. Then the
 -closure of X is defined recursively as
-closure of X is defined recursively as

 ( X ) .
( X ) .

 ( X ) , then
( X ) , then
 ( q ,
( q ,  )
)

 ( X ) .
( X ) .
 ( X ) unless it is
obtained by the Basis and Inductive Clauses.
( X ) unless it is
obtained by the Basis and Inductive Clauses.
 T )
T )

 ( S )
( S ) 
 ( T ) .
( T ) .

 ( S )
and T
( S )
and T 
 ( T ) ,
S and T are subsets of
( T ) ,
S and T are subsets of
 ( S )
( S ) 
 ( T ) .
Hence
( S
( T ) .
Hence
( S  T )
T )

 ( S )
( S ) 
 ( T ) .
( T ) .
 ( S
( S  T )
with the property of being in
T )
with the property of being in  ( S )
( S )

 ( T ) ,
then
( T ) ,
then
 ( q ,
( q ,
 )
)

 ( S )
( S ) 
 ( T ) .
( T ) .
 ( S
( S  T )
with the property of being in
T )
with the property of being in  ( S )
( S )

 ( T ) .
( T ) .

 ( S )
( S ) 
 ( T ) ,
q
( T ) ,
q 
 ( S ) or
q
( S ) or
q 
 ( T ) .
( T ) .

 ( S ) , then
( S ) , then
 ( q ,
( q ,
 )
)

 ( S ) by the definition of
( S ) by the definition of
 ( S ) . Hence
( S ) . Hence
 ( q ,
( q ,
 )
)

 ( S )
( S )

 ( T ) .
( T ) .

 ( T ) , then
( T ) , then
 ( q ,
( q ,
 )
)

 ( S )
( S )

 ( T ) .
( T ) .
 ( S
( S  T )
with the property of being in
T )
with the property of being in  ( S )
( S )

 ( T ) ,
then
( T ) ,
then
 ( q ,
( q ,
 )
)

 ( S )
( S ) 
 ( T ) .
( T ) .
 ( S
( S  T )
have the property of being in
T )
have the property of being in
 ( S )
( S ) 
 ( T ) which is to say that
( T ) which is to say that
 ( S
( S  T )
T )

 ( S )
( S ) 
 ( T ) .
( T ) .
 ( S )
( S ) 
 ( T )
( T )

 ( S
( S  T ) .
T ) .
 ( S )
( S )

 ( S
( S  T ) and
T ) and
 ( T )
( T )

 ( S
( S  T ) .
That would imply that
T ) .
That would imply that
 ( S )
( S ) 
 ( T )
( T )

 ( S
( S  T ) .
T ) .
 ( S )
( S )

 ( S
( S  T ) :
T ) :
 ( S ) .
( S ) .

 ( S
( S  T ) .
T ) .
 ( S
( S  T ) , and
( S
T ) , and
( S  T )
T )

 ( S
( S  T ) ,
S
T ) ,
S 
 ( S
( S  T ) .
T ) .
 ( S ) , if q is in
( S ) , if q is in
 ( S
( S  T ) ,
then
T ) ,
then  ( q ,
( q ,
 )
)

 ( S
( S  T ) .
T ) .
 ( S
( S  T )
and since
T )
and since  ( S
( S  T )
is a
T )
is a  -closure, by the definition of
-closure, by the definition of
 -closure
-closure  ( q ,
( q ,
 )
)

 ( S
( S  T ) .
T ) .
 ( S )
( S )

 ( S
( S  T )
has been proven.
T )
has been proven.
 ( T )
( T )

 ( S
( S  T ) holds.
T ) holds.
 ( S )
( S ) 
 ( T )
( T )

 ( S
( S  T ) holds.
T ) holds.
 (
(
 Si ) =
Si ) =

 ( Si ) .
( Si ) .
 (
(
 Si )
=
Si )
=  ( S1 ) and
( S1 ) and

 ( Si )
=
( Si )
=  ( S1 ) .
( S1 ) .
 (
(
 Si ) =
Si ) =

 ( Si )
holds for n = 1.
( Si )
holds for n = 1.
 (
(
 Si ) =
Si ) =

 ( Si )
holds for n. --- Inducion Hypothesis
( Si )
holds for n. --- Inducion Hypothesis
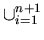
 ( Si )
= (
( Si )
= ( 
 ( Si ) )
( Si ) )

 ( Sn+1 )
by the definition of union.
( Sn+1 )
by the definition of union.
 (
(  Si )
Si )

 ( Sn+1 )
by the induction hypothesis.
( Sn+1 )
by the induction hypothesis.
 ( (
( (  Si )
Si )
 Sn+1 ) by Claim 2 above, since
Sn+1 ) by Claim 2 above, since  Si is a set as well as Sn+1.
Si is a set as well as Sn+1.
 (
( 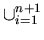 Si )
by the definition of union.
Si )
by the definition of union.

 : \delta
: \delta
 : \Lambda
: \Lambda
 : \Sigma
: \Sigma
 * : \Sigma^*
* : \Sigma^*
 : \cup
: \cup