Finite Automata
Application of Finite Automata
Subjects to be Learned
- Reactive system
- Modeling reactive systems with FA
Contents
We have seen an example of use of finite automata in describing the operation of a simplified version of vending machine. Many other systems operating in practice can also be modeled by finite automata such as control circuits of computers, computer network communication protocols, lexical analysers for compilers etc. Many of those systems fall into the class of systems called reactive system. A reactive system is a system that changes its actions, outputs
and conditions/status in response to stimuli from within or outside it.
It is an event driven or control driven system continuously having to react to external and/or internal stimuli.
The inputs for a reactive system are never ready unlike for example
when two numbers are added together by an adder (Here we are considering
an adder at a higher level of abstraction than physical devices level ignoring
for example the transient states of the electronic circuit
that realizes an adder).
An adder does not respond
unless the input i.e. two numbers to be added are ready. A system such as
an adder is called a transformational system. In the case of vending machine
or communication protocol, on the other hand, a system must respond
to each stimulus, even to a fragment of input such as each coin tossed in
for a can of soda or every message received.
It is generally agreed that finite automata are a natural medium to describe
dynamic behaviors of reactive systems. Finite automata are formal and rigorous
and computer programs can be easily written to simulate their behaviors.
To model a reactive system with finite automaton, first the states the system
goes in or the modes of its operation are identified. These become the states
of the finite automaton that models it.
Then the transitions between the states triggered by events and conditions,
external or internal to the system, are identified and they become arcs
in the transition diagram of the finite automaton. In addition actions that
may take place in those states can also be added to the model.
For example consider the following very simplified version of login process
to a computer from the computer point of view. Let us assume for simplicity
that this computer accepts a single user at a time.
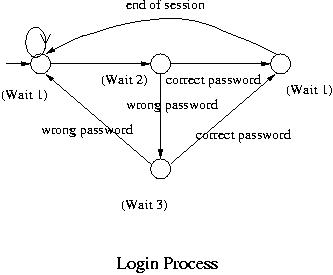
Initially the computer waits for a user name to be typed in. This is one state of
the system. When a name is typed in, it checks whether or not the name is valid.
If it is valid, then it asks for and then waits for the password, which is
another state.
If the user name typed in is not valid, it goes back to the initial state.
We could make it go to a different state
and count the number of login attempts for security purpose. But let us make it
simple. When a password is typed in and it is correct, then it accepts the user
and starts a session. That is another state though it could further be broken
down into a number of more states. When the session terminates, it gets a signal,
goes back
to the initial state and waits for another login. If the password typed in is
incorrect, then it informs the user of that and waits for the next try. That is
a fourth state. If the second password fails, it goes to the initial state and
starts all over again. Again what we have seen is a model for one level of
abstraction.
Depending on how much detail we are interested in, different states would be
identified and transitions would have to be selected accrdingly.
The next example is a protocol for a computer to follow in communicating
with another computer. Again it is a very simplified version.
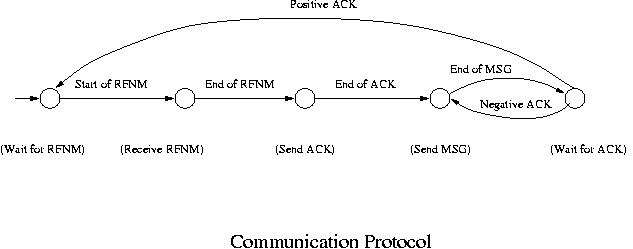
Initially the computer is in wait state waiting for "Request for Next Message"
(RFNM) to come from another computer. When a RFNM starts coming, it goes
into the state of
receiving it (Our interpretation is that the computer is in a state of receiving
an RFNM and it is taking the action of receiving the RFNM) .
Upon completion of the RFNM, it sends "Acknowledgement" (ACK) to the other
computer, which is another state. After sending the ACK, it starts sending
the requested message
to the other party. When it is complete, it goes into another wait state waiting
for
an ACK to come from the other computer. If a negative ACK is received, it resends
the message. If a positive ACK is received, it goes back to the initial state
and waits for another RFNM to come. Thus a finite automaton that models this
protocol has the following five states: initial state (wait for RFNM),
receiving RFNM, sending ACK, sending message and waiting for ACK.
Again depending on the level of abstraction, different states and transitions
would have to be chosen.
Our third example is a system that recognizes numbers with or without a sign
such as 5.378, -15, +213.8 etc.
One such system initially waits for the first symbol to come in. If the first symbol is a sign, then it goes into a state, denote it by G, that indicates that a sign has been received.
If the first digit is received before a decimal point, regardless of whether a sign has been read or not, it goes into a state, denote it by D, that indicates a digit has been read before a decimal point.
If a decimal point is received before a digit, then it goes into a state, denote it by P, that indicates that a decimal point has been read.
If a decimal point has been read (i.e. in state P), then it must receive at least one digit after that. After one digit it can continue receiving digits. Therefore from state P it goes to another state, denote it by Q, after reading a digit and stays there as long as digits are read. This Q is an accepting state.
On the other hand if a digit has been read before a decimal point, i.e. it is in state D, then it can continue receiving digits and stay in D. D is another accepting state. If a decimal point is read while in D, then it goes to state P
indicating that a decimal point has been read.
This system can also be described by a regular expression.
Since these numbers are represented by strings consisting of a possible sign, followed by zero or more digits, followed by a possible decimal point, followed by one or more digits, they can be represented by the following regular expression:
( s+ + s- +  ) ( d+.d+ +
d+ + .d+ ),
) ( d+.d+ +
d+ + .d+ ),
where s+ and s-
represent the positive and negative signs, respectively and d  { 0 , 1 , 2 , . . . , 9 } .
This system can be modeled by the following finite automaton:
{ 0 , 1 , 2 , . . . , 9 } .
This system can be modeled by the following finite automaton:
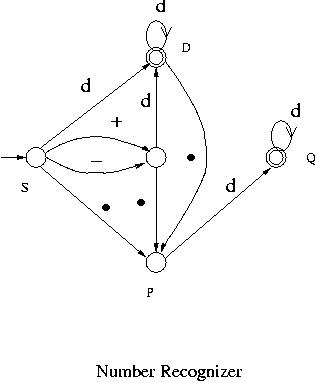
Next -- Simulation of FA
Back to Study Schedule
Back to Table of Contents


 ) ( d+.d+ +
d+ + .d+ ),
) ( d+.d+ +
d+ + .d+ ),
 { 0 , 1 , 2 , . . . , 9 } .
This system can be modeled by the following finite automaton:
{ 0 , 1 , 2 , . . . , 9 } .
This system can be modeled by the following finite automaton:
