Finite Automata
Kleene's Theorem --- Part 1
Subjects to be Learned
- Union of FAs
- Concatenation of FAs
- Kleene Star of FAs
- Acceptance of regular languages by FAs
Contents
In this unit we are going to learn Kleene's theorem. It states that any regular language is accepted by an FA
and conversely that any language accepted by an FA is regular.
Theorem 1 (Part 1 of Kleene's theorem):
Any regular language is accepted by a finite automaton.
Proof: This is going to be proven by (general) induction following
the recursive definition of regular language.
Basis Step:
As shown below the languages
 ,
{
,
{ } and
{ a } for any symbol a in
} and
{ a } for any symbol a in  are accepted by an FA.
are accepted by an FA.
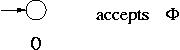
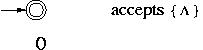

Inductive Step: We are going to show that for any languages L1 and L2
if they are accepted by FAs, then L1 L2 ,
L1L2 and L1* are accepted by FAs.
Since any regular language is obtained from
{
L2 ,
L1L2 and L1* are accepted by FAs.
Since any regular language is obtained from
{ } and
{ a } for any symbol a in
} and
{ a } for any symbol a in  by using union, concatenation and Kleene star operations,
that together with the Basis Step would prove the theorem.
by using union, concatenation and Kleene star operations,
that together with the Basis Step would prove the theorem.
Suppose that L1 and L2 are accepted by FAs M1 = < Q1 ,  ,
q1,0 ,
,
q1,0 ,  1 , A1 >
and M2 = < Q2 ,
1 , A1 >
and M2 = < Q2 ,  ,
q2,0 ,
,
q2,0 ,  2 , A2 > , respectively.
We assume that Q1
2 , A2 > , respectively.
We assume that Q1  Q2 =
Q2 =  without loss of generality since states can be renamed if necessary.
without loss of generality since states can be renamed if necessary.
Then L1 L2 ,
L1L2 and L1* are accepted by the FAs
Mu = < Qu ,
L2 ,
L1L2 and L1* are accepted by the FAs
Mu = < Qu ,  ,
qu,0 ,
,
qu,0 ,  u , Au >
, Mc = < Qc ,
u , Au >
, Mc = < Qc ,  ,
qc,0 ,
,
qc,0 ,  c , Ac >
and Mk = < Q2 ,
c , Ac >
and Mk = < Q2 ,  ,
qk,0 ,
,
qk,0 ,  k , Ak > , respectively, which are given below.
k , Ak > , respectively, which are given below.
Mu = < Qu ,  ,
qu,0 ,
,
qu,0 ,  u , Au > :
u , Au > :
Qu = Q1  Q2
Q2  { qu,0 } , where qu,0 is a state which is neither in Q1 nor in Q2 .
{ qu,0 } , where qu,0 is a state which is neither in Q1 nor in Q2 .
 u =
u =  1
1

 2
2
 { (qu,0,
{ (qu,0,  , { q1,0 , q2,0 } ) } ,
that is
, { q1,0 , q2,0 } ) } ,
that is  u(qu,0,
u(qu,0,  ) =
{ q1,0 ,
q2,0 } . Note that
) =
{ q1,0 ,
q2,0 } . Note that  u(qu,0, a ) =
u(qu,0, a ) =
 for all a in
for all a in  .
.
Au = A1  A2
A2
Mc = < Qc ,  ,
qc,0 ,
,
qc,0 ,  c , Ac > :
c , Ac > :
Qc = Q1  Q2
Q2
qc,0 = q1,0
 c =
c =  1
1

 2
2
 { (q,
{ (q,  , { q2,0 } ) | q
, { q2,0 } ) | q  A1 }
A1 }
Ac = A2
Mk = < Qk ,  ,
qk,0 ,
,
qk,0 ,  k , Ak > :
k , Ak > :
Qk = Q1  { qk,0 } , where qk,0 is a state which is not in Q1 .
{ qk,0 } , where qk,0 is a state which is not in Q1 .
 k =
k =  1
1
 { (qk,0,
{ (qk,0,  , { q1,0 } ) }
, { q1,0 } ) }
 { (q,
{ (q,  , { qk,0 } ) | q
, { qk,0 } ) | q  A1 }
A1 }
Ak = { qk,0 }
These NFA- s are illustrated below.
s are illustrated below.
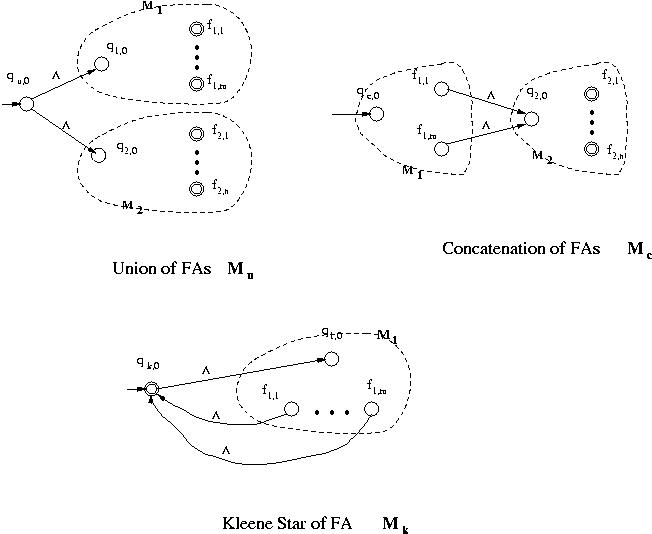
It can be proven, though we omit proofs, that these NFA- s , Mu, Mc
and Mk , in fact accept L1
s , Mu, Mc
and Mk , in fact accept L1 L2 ,
L1L2 and L1*, respectively.
L2 ,
L1L2 and L1*, respectively.
End of Proof
Examples of Mu , Mc
and Mk:
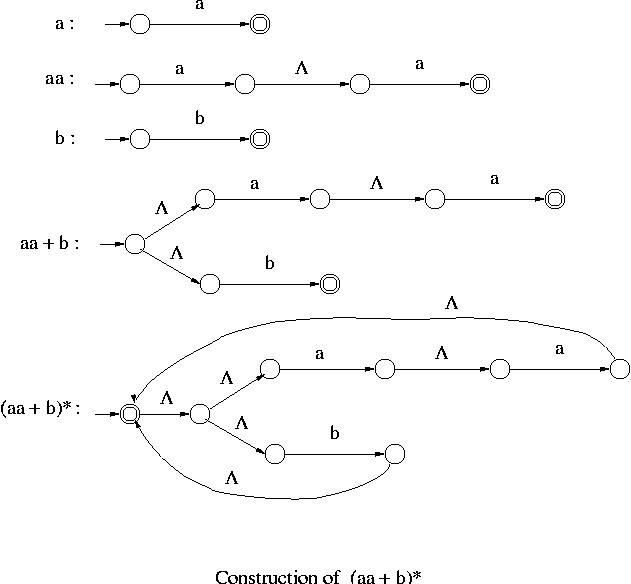
Example 1:
An NFA- that accepts the language represented by the regular expression
(aa + b)* can be constructed as follows using the operations given above.
that accepts the language represented by the regular expression
(aa + b)* can be constructed as follows using the operations given above.
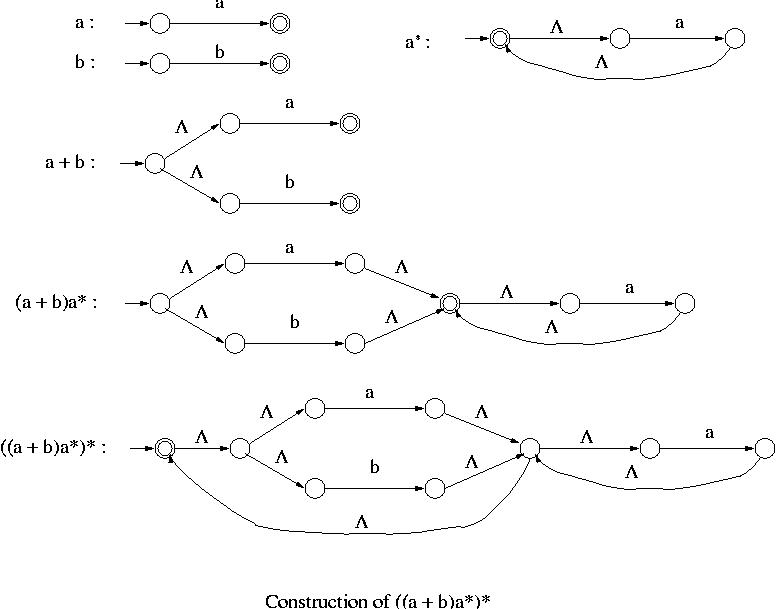
Example 2:
An NFA- that accepts the language represented by the regular expression
((a + b)a*)* can be constructed as follows using the operations given above.
that accepts the language represented by the regular expression
((a + b)a*)* can be constructed as follows using the operations given above.
Test Your Understanding of Kleene's Theorem Part 1
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.
Next -- Kleene's Theorem --- Part 2
Back to Study Schedule
Back to Table of Contents
 ,
{
,
{ } and
{ a } for any symbol a in
} and
{ a } for any symbol a in  are accepted by an FA.
are accepted by an FA.
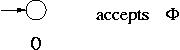
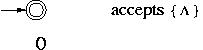

 L2 ,
L1L2 and L1* are accepted by FAs.
Since any regular language is obtained from
{
L2 ,
L1L2 and L1* are accepted by FAs.
Since any regular language is obtained from
{ } and
{ a } for any symbol a in
} and
{ a } for any symbol a in  by using union, concatenation and Kleene star operations,
that together with the Basis Step would prove the theorem.
by using union, concatenation and Kleene star operations,
that together with the Basis Step would prove the theorem.
 ,
q1,0 ,
,
q1,0 ,  1 , A1 >
and M2 = < Q2 ,
1 , A1 >
and M2 = < Q2 ,  ,
q2,0 ,
,
q2,0 ,  2 , A2 > , respectively.
We assume that Q1
2 , A2 > , respectively.
We assume that Q1 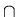 Q2 =
Q2 =  without loss of generality since states can be renamed if necessary.
without loss of generality since states can be renamed if necessary.
 L2 ,
L1L2 and L1* are accepted by the FAs
Mu = < Qu ,
L2 ,
L1L2 and L1* are accepted by the FAs
Mu = < Qu ,  ,
qu,0 ,
,
qu,0 ,  u , Au >
, Mc = < Qc ,
u , Au >
, Mc = < Qc ,  ,
qc,0 ,
,
qc,0 ,  c , Ac >
and Mk = < Q2 ,
c , Ac >
and Mk = < Q2 ,  ,
qk,0 ,
,
qk,0 ,  k , Ak > , respectively, which are given below.
k , Ak > , respectively, which are given below.
 ,
qu,0 ,
,
qu,0 ,  u , Au > :
u , Au > :
 Q2
Q2  { qu,0 } , where qu,0 is a state which is neither in Q1 nor in Q2 .
{ qu,0 } , where qu,0 is a state which is neither in Q1 nor in Q2 .
 u =
u =  1
1

 2
2
 { (qu,0,
{ (qu,0,  , { q1,0 , q2,0 } ) } ,
that is
, { q1,0 , q2,0 } ) } ,
that is  u(qu,0,
u(qu,0,  ) =
{ q1,0 ,
q2,0 } . Note that
) =
{ q1,0 ,
q2,0 } . Note that  u(qu,0, a ) =
u(qu,0, a ) =
 for all a in
for all a in  .
.
 A2
A2
 ,
qc,0 ,
,
qc,0 ,  c , Ac > :
c , Ac > :
 Q2
Q2
 c =
c =  1
1

 2
2
 { (q,
{ (q,  , { q2,0 } ) | q
, { q2,0 } ) | q  A1 }
A1 }
 ,
qk,0 ,
,
qk,0 ,  k , Ak > :
k , Ak > :
 { qk,0 } , where qk,0 is a state which is not in Q1 .
{ qk,0 } , where qk,0 is a state which is not in Q1 .
 k =
k =  1
1
 { (qk,0,
{ (qk,0,  , { q1,0 } ) }
, { q1,0 } ) }
 { (q,
{ (q,  , { qk,0 } ) | q
, { qk,0 } ) | q  A1 }
A1 }
 s are illustrated below.
s are illustrated below.

 s , Mu, Mc
and Mk , in fact accept L1
s , Mu, Mc
and Mk , in fact accept L1 L2 ,
L1L2 and L1*, respectively.
L2 ,
L1L2 and L1*, respectively.
 that accepts the language represented by the regular expression
(aa + b)* can be constructed as follows using the operations given above.
that accepts the language represented by the regular expression
(aa + b)* can be constructed as follows using the operations given above.

 that accepts the language represented by the regular expression
((a + b)a*)* can be constructed as follows using the operations given above.
that accepts the language represented by the regular expression
((a + b)a*)* can be constructed as follows using the operations given above.
