Turing Machines
Turing Machines
Subjects to be Learned
- Definition of Turing Machine
- Configuration
- Operation of Turing Machine
Contents
Introduction
We have studied two types of languages from the Chomsky hierarchy: regular languages
and context-free languages. These languages can describe many practically important
systems and so they are heavily used in practice.
They are, however, of limited capability and there are many languages that they can
not process.
In this chapter we are going to study the most general of the languages in Chomsky
hierarchy, the phrase structure languages (also called Type 0 languages), and the machines
that can process them:
Turing machines.
Turing machines were conceived of by the English mathematician Alan Turing as a model
of human "computation". Later Alonzo Church conjectured
that any computation done by humans or computers can be carried out by some Turing machine.
This conjecture is known as Church's thesis and today it is generally accepted as true.
Computers we use today are as powerful as Turing machines except that computers have finite memory
while Turing machines have infinite memory.
We are going to study Turing machines here and through that limitations of computers and computation
as we know today.
Definition
Conceptually a Turing machine, like finite automata, consists of a finite control and
a tape. At any time it is in one of the finite number of states. The tape has the left
end but it extends infinitely to the right.
It is also divided into squares and
a symbol can be written in each square. However, unlike finite automata, its head is a read-write
head and it
can move left, right or stay at the same square after a read or write.
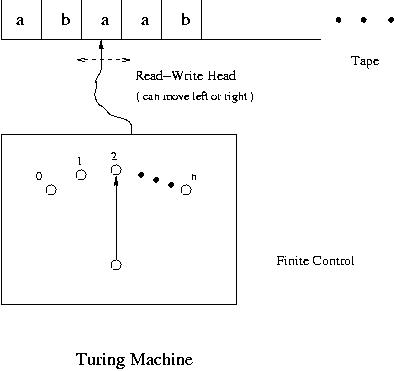
Given a string of symbols on the tape, a Turing machine starts at the initial state.
At any state it reads the symbol under the head, either erases it or replaces it
with a symbol (possibly the same symbol). It then moves the head to left or right or
does not move it and goes to the next state which may be the same as the current state.
One of its states is the halt state and when the Turing machine goes into the halt state,
it stops its operation.
Formally a Turing machine is a 5-tuple T = < Q,  ,
,
 , q0,
, q0,  > ,
where
> ,
where
Q is a finite set of states, which is assumed not to contain the symbol h.
The symbol h is used to denote the halt state.
 is a finite set of symbols and it is the input alphabet.
is a finite set of symbols and it is the input alphabet.
 is a finite set of symbols containing
is a finite set of symbols containing  as its subset and it is the set of tape symbols.
as its subset and it is the set of tape symbols.
q0 is the initial state.
 is the transition function but its value may not be defined
for certain points.
is the transition function but its value may not be defined
for certain points.
It is a mapping from Q  (
( 
 {
{ } ) to ( Q
} ) to ( Q  { h } )
{ h } )
 (
( 
 {
{ } )
} )  { R , L , S } .
{ R , L , S } .
Here  denotes the blank and R, L and S denote move the head right,
left and do not move it, respectively. A transition diagram can also be drawn for a Turing machine.
The states are represented by vertices and for a transition
denotes the blank and R, L and S denote move the head right,
left and do not move it, respectively. A transition diagram can also be drawn for a Turing machine.
The states are represented by vertices and for a transition
 ( q, X ) = ( r, Y, D ) , where D represents R, L or S , an arc from q to r
is drawn with label ( X/Y , D ) indicating that the state is changed from q to r, the symbol X
currently being read is changed to Y and the tape head is moved as directed by D.
( q, X ) = ( r, Y, D ) , where D represents R, L or S , an arc from q to r
is drawn with label ( X/Y , D ) indicating that the state is changed from q to r, the symbol X
currently being read is changed to Y and the tape head is moved as directed by D.
Example 1 :
The following Turing machine < Q1 ,  ,
,
 , q0 ,
, q0 ,  > accepts
the language aba* , where
Q1 = { q0, q1, q2, q3 } ,
> accepts
the language aba* , where
Q1 = { q0, q1, q2, q3 } ,
 = { a , b } ,
= { a , b } ,
 = { a , b }
and
= { a , b }
and  is as given by the table below.
is as given by the table below.
| State (q) | Input (X) | Move (  (q, X) )
(q, X) ) |
q0 |  |
( q1 ,  , R ) , R ) |
q1 | a | ( q2 , a , R ) |
q2 | b | ( q3 , b , R ) |
q3 | a | ( q3 , a , R ) |
q3 |  |
( h ,  , S ) , S ) |
A transition diagram of this Turing machine is given below.
It is assumed that the tape has  at the left end
and the head is initially at the left end of the tape.
at the left end
and the head is initially at the left end of the tape.

Turing Machine that accepts aba*
To describe the operation of Turing machine we use configuration.
A configuration for a Turing machine is an ordered pair
of the current state
and the tape contents with the symbol currently under the head marked with underscore. For example ( q , aababb ) shows that the Turing machine is
currently in state q, the taper contents are the string aababb and the head is reading
the last a of the string.
We write ( p , xay )  ( q , zbw ) if the Turing machine goes from the first
configuration to the second in one move, and ( p , xay )
( q , zbw ) if the Turing machine goes from the first
configuration to the second in one move, and ( p , xay )
 *
( q , zbw ) if the Turing machine goes from the first
configuration to the second in zero or more moves. If the Turing machine needs to be
explicitly indicated
*
( q , zbw ) if the Turing machine goes from the first
configuration to the second in zero or more moves. If the Turing machine needs to be
explicitly indicated  T or
T or
 T* is used.
T* is used.
A string x is said to be accepted by a Turing machine*
T = < Q ,  ,
,  , q0 ,
, q0 ,
 > if
> if
( q0 ,  x )
x )
 *
( h, yaz ) for some symbol a
*
( h, yaz ) for some symbol a 

 {
{ }
and some strings y and z in (
}
and some strings y and z in ( 
 {
{ } )*.
In this case we also say that the Turing machine halts on input x.
The set of strings accepted by a Turing machine is the language accepted
by the Turing machine.
Note that the Turing machine does not stop if a string is not in the language.
A Turing machine T is said to decide a language L if and only if T writes "yes" and halts if a string is in L and T writes "no" and halts if a string is not in L.
} )*.
In this case we also say that the Turing machine halts on input x.
The set of strings accepted by a Turing machine is the language accepted
by the Turing machine.
Note that the Turing machine does not stop if a string is not in the language.
A Turing machine T is said to decide a language L if and only if T writes "yes" and halts if a string is in L and T writes "no" and halts if a string is not in L.
For example the Turing machine of Example 1 above goes through the following sequence of
configurations
to accept the string aba:
( q0 ,  aba )
aba )
 ( q1 ,
( q1 , aba )
aba )
 ( q2 ,
( q2 , aba )
aba )
 ( q3 ,
( q3 , aba )
aba )
 ( h ,
( h , aba
aba )
)
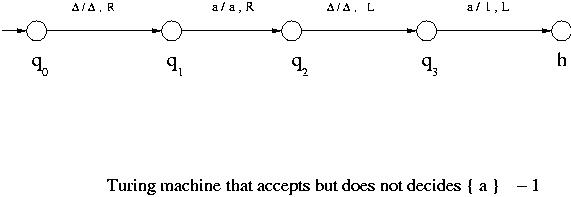
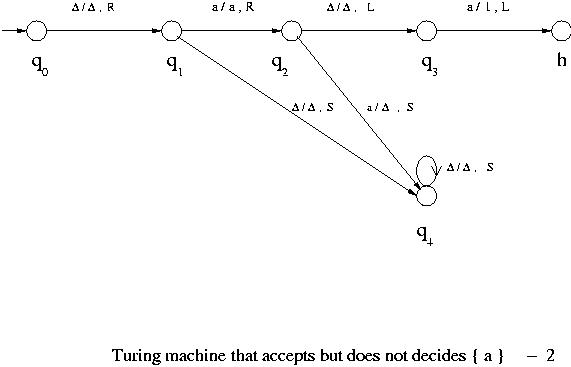
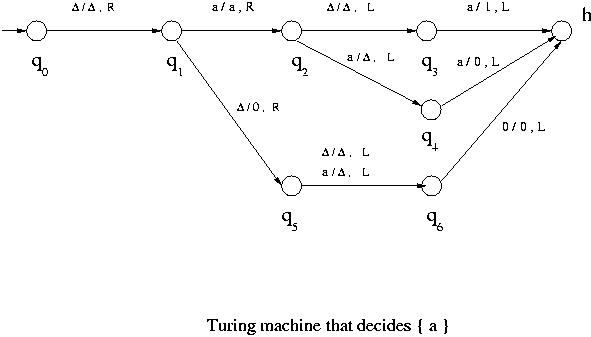
The first of the following figures shows a Turing machine that accepts but does not decide the language { a },
the second is a Turing machine that accepts { a } but goes into a loop if a string is not in the language (hence it accepts but doe not decide { a }) and the third decides { a }, where  = { a }.
= { a }.
Example 2 :
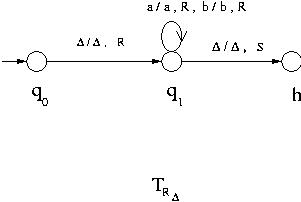
The following Turing machine moves the head to the first  to the right of the current position.
It is denoted by TR
to the right of the current position.
It is denoted by TR .
.
Example 3 :
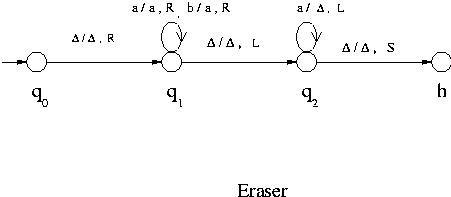
The following Turing machine erases the string on the tape and moves the head to the left end. It is assumed that initially the tape has  at the left end.
This Turing machine is denoted by TE.
at the left end.
This Turing machine is denoted by TE.
Strings not Accepted by Turing Machines
When a string is not accepted by a Turing machine, that is
when a Turing machine does not halt on a string, one of
the following three things happens:
(1) The Turing machine goes into an infinite loop,
(2) no transition is specified for the current configuration and
(3) the head is at the left end and it is instructed to move left.
In cases (2) and (3), the operation of the Turing machine
is aborted. For example the following Turing machine accepts the
language a+, but it goes into an infinite loop for any
strings that are not in the language.
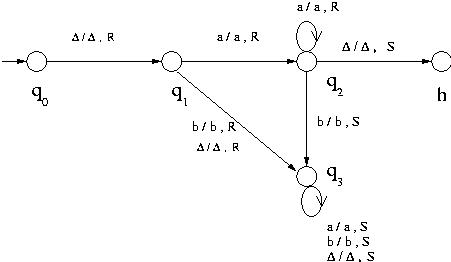
Turing machine accepting a+
Computabler Function
Let S 
 * and
let f be a function f : S ->
* and
let f be a function f : S ->  *. Then we say T computes
f or
f is computable if for every
x
*. Then we say T computes
f or
f is computable if for every
x  S,
S,
( q0 ,  x )
x )
 *
( h,
*
( h,  f(x) )
f(x) )
and for every x 
 *
that is not in S, T does not halt on x.
*
that is not in S, T does not halt on x.
* Note on "Turing-acceptable": Some books define "acceptance by Turing machine" slightly differently.
That is, in the Turing machines those books define, there are two halt states: "accept halt"
and "reject halt". A Turing machine thus may accept a string and halt, reject a string and halt, or loop.
With this definition, a string is accepted
by a Turing machine if given the string, the Turing machine eventually
goes into
the accept halt state.
As far as the material discussed in this class note, there is no difference
between these two definitions of "accept".
A language is a phrase structure (type 0) langauage if and only if it is
Turing-acceptable in either sense and it has no effects on decidablility.
Test Your Understanding of Turing Machines
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.
There are two sets of questions.
Next -- Combination of Turing Machines
Back to Study Schedule
Back to Table of Contents
 (q, X) )
(q, X) )
 , R )
, R )
 , S )
, S )
 ,
,
 , q0,
, q0,  > ,
where
> ,
where
 is a finite set of symbols and it is the input alphabet.
is a finite set of symbols and it is the input alphabet.
 is a finite set of symbols containing
is a finite set of symbols containing  as its subset and it is the set of tape symbols.
as its subset and it is the set of tape symbols.
 is the transition function but its value may not be defined
for certain points.
is the transition function but its value may not be defined
for certain points.
 (
( 
 {
{ } ) to ( Q
} ) to ( Q  { h } )
{ h } )
 (
( 
 {
{ } )
} )  { R , L , S } .
{ R , L , S } .
 denotes the blank and R, L and S denote move the head right,
left and do not move it, respectively. A transition diagram can also be drawn for a Turing machine.
The states are represented by vertices and for a transition
denotes the blank and R, L and S denote move the head right,
left and do not move it, respectively. A transition diagram can also be drawn for a Turing machine.
The states are represented by vertices and for a transition
 ( q, X ) = ( r, Y, D ) , where D represents R, L or S , an arc from q to r
is drawn with label ( X/Y , D ) indicating that the state is changed from q to r, the symbol X
currently being read is changed to Y and the tape head is moved as directed by D.
( q, X ) = ( r, Y, D ) , where D represents R, L or S , an arc from q to r
is drawn with label ( X/Y , D ) indicating that the state is changed from q to r, the symbol X
currently being read is changed to Y and the tape head is moved as directed by D.
 ,
,
 , q0 ,
, q0 ,  > accepts
the language aba* , where
Q1 = { q0, q1, q2, q3 } ,
> accepts
the language aba* , where
Q1 = { q0, q1, q2, q3 } ,
 = { a , b } ,
= { a , b } ,
 = { a , b }
and
= { a , b }
and  is as given by the table below.
is as given by the table below.
 (q, X) )
(q, X) )
 , R )
, R )
 , S )
, S ) at the left end
and the head is initially at the left end of the tape.
at the left end
and the head is initially at the left end of the tape.

 ( q , zbw ) if the Turing machine goes from the first
configuration to the second in one move, and ( p , xay )
( q , zbw ) if the Turing machine goes from the first
configuration to the second in one move, and ( p , xay )
 *
( q , zbw ) if the Turing machine goes from the first
configuration to the second in zero or more moves. If the Turing machine needs to be
explicitly indicated
*
( q , zbw ) if the Turing machine goes from the first
configuration to the second in zero or more moves. If the Turing machine needs to be
explicitly indicated  T or
T or
 T* is used.
T* is used.
 ,
,  , q0 ,
, q0 ,
 > if
> if
 x )
x )
 *
( h, yaz ) for some symbol a
*
( h, yaz ) for some symbol a 

 {
{ }
and some strings y and z in (
}
and some strings y and z in ( 
 {
{ } )*.
In this case we also say that the Turing machine halts on input x.
The set of strings accepted by a Turing machine is the language accepted
by the Turing machine.
Note that the Turing machine does not stop if a string is not in the language.
A Turing machine T is said to decide a language L if and only if T writes "yes" and halts if a string is in L and T writes "no" and halts if a string is not in L.
} )*.
In this case we also say that the Turing machine halts on input x.
The set of strings accepted by a Turing machine is the language accepted
by the Turing machine.
Note that the Turing machine does not stop if a string is not in the language.
A Turing machine T is said to decide a language L if and only if T writes "yes" and halts if a string is in L and T writes "no" and halts if a string is not in L.
 aba )
aba )
 ( q1 ,
( q1 , aba )
aba )
 ( q2 ,
( q2 , aba )
aba )
 ( q3 ,
( q3 , aba )
aba )
 ( h ,
( h , aba
aba )
)
 = { a }.
= { a }.



 to the right of the current position.
It is denoted by TR
to the right of the current position.
It is denoted by TR .
.

 at the left end.
This Turing machine is denoted by TE.
at the left end.
This Turing machine is denoted by TE.



 * and
let f be a function f : S ->
* and
let f be a function f : S ->  *. Then we say T computes
f or
f is computable if for every
x
*. Then we say T computes
f or
f is computable if for every
x  S,
S,
 x )
x )
 *
( h,
*
( h,  f(x) )
f(x) )

 *
that is not in S, T does not halt on x.
*
that is not in S, T does not halt on x.