Predicate Logic
Universal Instantiation
Subjects to be Learned
- universal instantiation rule
Contents
Rule:
 x P(x)
x P(x)
-------
P(c)
where c is some arbitrary element of the universe.
Restrictions:
If c is a variable, then it must not already be quantified somewhere
in P(x) --- see Explanation and Note below.
Explanation:
What this rule says is that from
 x P(x)
one can infer P(c) for any object in the universe represented by the variable c,
thus stripping off the universal quantifier. It should be noted that P holds for any
specifc object in the universe in this case. This rule follows because
x P(x)
one can infer P(c) for any object in the universe represented by the variable c,
thus stripping off the universal quantifier. It should be noted that P holds for any
specifc object in the universe in this case. This rule follows because
 x P(x) says that P(x) holds
true for all objects in the universe.
Note that P(x), in general, may be a compound wff invloving a number of predicates,
variables, and quantifiers. Thus c in P(c) must not be a variable which is quantified
within P(x). See Note below for an example of what can happen c is not properly chosen.
x P(x) says that P(x) holds
true for all objects in the universe.
Note that P(x), in general, may be a compound wff invloving a number of predicates,
variables, and quantifiers. Thus c in P(c) must not be a variable which is quantified
within P(x). See Note below for an example of what can happen c is not properly chosen.
Example:
For example, the following argument can be proven correct using the Universal
Instantiation:"No humans can fly. John Doe is human. Therefore John Doe can not fly."
First let us express this using the following notation:
F(x) means "x can fly."
H(x) means "x is human."
d is a symbol representing John Doe.
Then the argument is
[ x
[H(x)
x
[H(x)
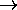
 F(x)]
F(x)]
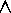 H(d) ]
H(d) ]
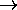
 F(d).
F(d).
The proof is
1.  x
[H(x) x
[H(x)
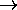
 F(x)]
F(x)]
|
Hypothesis
|
|
2. H(d)
|
Hypothesis
|
3. H(d)
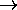
 F(d)
F(d)
|
Universal instantiation on 1.
|
4.  F(d)
F(d)
|
Modus ponens on 2 and 3.
|
Note:
If the restriction on the Universal Instantiation does not exist, then
 y
y
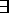 x P(x,y)
may become
x P(x,y)
may become
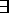 x P(x,x),
that is x has been substituted for y by the Universal Instantiation, which is
not correct.
x P(x,x),
that is x has been substituted for y by the Universal Instantiation, which is
not correct.