Practice Questions on Recursive Definition
Recursive Definition
More Examples on Recursive Definition of Set
Example 1. Recursively define the set S =
{n2 | n is a natural number greater
than 0}, that is S = {1, 4, 9, 16, ... }.
S is the set that is defined by the following clauses:
Basis Clause: 1 is in S.
Inductive Clause: If x
in S, then x + 2x1/2 + 1 is
in S.
Extremal Clause: Nothing is in S
unless it is obtained
from the Basis and Inductive Clauses.
How do we get x + 2x1/2 + 1 in the
Inductive Clause ?
Since S = {1, 4, 9, 16, ... }and its elements can be ordered
1, 4, 9, ..., n2 , for the n-th element,
which is n2, the next element is
(n+1)2. Hence if we let x be the
n-th element, then x = n2.
Hence n = x1/2. But the element next to x is
(n+1)2 which is equal to n2 +
2n + 1. By substituting n = x1/2 into that
we obtain x + 2x1/2 + 1.
Example 2. Recursively define the set T = {2n - 2 |
n is a natural number greater than 0}, that is T =
{0, 2, 6, 14, 30, ... }.
T is the set that is defined by the following clauses:
Basis Clause: 0 is in T.
Inductive Clause: If x is
in T,
then 2x + 2 is in T.
Extremal Clause: Nothing is in T
unless it is obtained from the Basis and Inductive Clauses.
How do we get 2x + 2 in the Inductive Clause ?
Since T = {0, 2, 6, 14, ... } and its elements can be ordered
0, 2, 6, ..., 2n - 2, for the n-th element,
which is 2n - 2, the next element is 2n+1 - 2.
Hence if we let x be the n-th element, then
x = 2n - 2. Now 2n+1 - 2 = 2*2n - 2
= 2*(2n - 2) + 2 = 2x + 2.
Example 3. Recursively define the set of strings U =
{anbcn |
n is a natural number}, that is U is the set {b,
abc,
aabcc, ... }.
Since the simplest element in U is b, let us select
b as the basis element. Then from b we can obtain
abc by prepending a
and appending c to it. Similarly
aabcc
can be obtained from abc by
prepending a
and appending c to it. Similarly for the rest of the elements of
the set U. Thus U is the set that satisfy the following clauses:
Basis Clause: b is in U.
Inductive Clause: If x is in U, then
axc is in U.
Extremal Clause: Nothing is in U
unless it is obtained from the Basis and Inductive Clauses.
Example 4. Recursively define the set V = {x | x
is a natural number and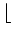 
x/2
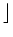is even},
that is x = {0, 4, 8, 12, 16, ... }.
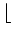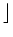Note that x denotes the largest integer
that is not larger than x. If x is nonnegative as in this
example, it is the integer part of x.
Since 0 is the smallest element of x, let us select 0
as the basis element of V. For the inductive clause note that
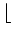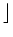for x to increase by 2 to the next
even number, x needs to grow by 4. Hence we have the following
definition for V:
V is the set that is defined by the following clauses:
Basis Clause: 0 is in V.
Inductive Clause: If x is in V, then
x + 1 is in V.
Extremal Clause: Nothing is in V
unless it is obtained from the Basis and Inductive Clauses.
We have defined four sets recursively. However, we are at this point not exactly
sure whether or not those definitions correctly define the sets. To verify those
definitions, that is, to check whether or not the elements of each set have the
specified properties, we can use proof by induction.
Let us try to verify the definition of Example 1.
Verification of Definition of set S:
To verify the definition of Example 1 we are going to prove by
(general) induction that the elements
of the set S is in the form
n2, where n is a natural number greater
than 0.
In the Basis Step we prove that the element in the basis, that is 1 in this case,
has the property. Then in the Inductive Step we prove that if an arbitrary
element,say x, has the property, then the element generated from
x has the property.
Basis Step: Since 1 = 12, the basis element 1 of the set
S is of the form n2, where n is a
natural number greater than 0.
Inductive Step: Let x be an arbitrary element of S and
x = n2 for some
natural number n. Then the element generated from
x by the Inductive Clause of the definition of
S is x + 2x1/2 + 1.
We are trying to show that x + 2x1/2 + 1
is of the form n2.
Since x = n2, x1/2 = n.
Hence
x + 2x1/2 + 1 = n2 + 2n + 1 =
(n + 1)2, which is the square of a natural number
n + 1.
End of the proof.
Next let us try to verify the definition of Example 3.
Verification of Definition of set U:
To verify the definition of Example 3 we are going to prove by
(general) induction that the elements
of the set U is in the form anbcn
, where n is a natural number.
In the Basis Step we prove that the element in the basis, that is b
in this case,
has the property. Then in the Inductive Step we prove that if an arbitrary
element, say x, has the property, then the element generated from
x has the property.
Basis Step: b is in the form
anbcn with n = 0.
Inductive Step: Let x be an arbitrary element of U and
x = anbcn for some
natural number n. Then the element generated from
x by the Inductive Clause of the definition of
U is axc which is equal to
aanbcnc, which in turn is equal to
a(n+1)bc(n+1). Hence if an arbitrary
element x has the property, then its children also have the property.
End of the proof.
The sets of Examples 2 and 4 can also be verified similarly. They are left as exercises.
Back to Table of Contents