Relation
Equality of Relations
Subjects to be Learned
- equality of binary relations
- equality of n-ary relations
Contents
Definition (equality of binary relation):
Two binary relations
R1
 A1
A1
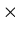 A2
and
R2
A2
and
R2
 B1
B1
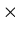 B2
are equal if and only if
A1 = B1 , A2 = B2 ,
and R1 = R2 as a set.
B2
are equal if and only if
A1 = B1 , A2 = B2 ,
and R1 = R2 as a set.
For example, let
R1 = {<1, 2> , <2, 2>}
 {1, 2}
{1, 2}
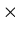 {1, 2} ,
and
R2 = {<a, b> , <b, b>}
{1, 2} ,
and
R2 = {<a, b> , <b, b>}
 {a, b}
{a, b}
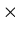 {a, b} .
Then R1 = R2 if and only if a = 1 and
b = 2.
{a, b} .
Then R1 = R2 if and only if a = 1 and
b = 2.
Definition (equality of n-ary relation):
An n-ary relation
R1
 A1
A1
 ...
...
 An
and
an m-ary relation
R2
An
and
an m-ary relation
R2
 B1
B1
 ...
...
 Bm
are equal
if and only if m = n, Ai = Bi
for each i,
1
Bm
are equal
if and only if m = n, Ai = Bi
for each i,
1
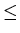 i
i
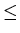 n , and
R1 = R2 as a set of ordered n-tuples.
n , and
R1 = R2 as a set of ordered n-tuples.
Test Your Understanding of Equality of Relations
Indicate which of the following statements are correct and which are not.
Click True or False , then Submit. There is one set of questions.
Next -- Digraph
Back to Schedule
Back to Table of Contents
![]() {1, 2}
{1, 2}
![]() {1, 2} ,
and
R2 = {<a, b> , <b, b>}
{1, 2} ,
and
R2 = {<a, b> , <b, b>}
![]() {a, b}
{a, b}
![]() {a, b} .
Then R1 = R2 if and only if a = 1 and
b = 2.
{a, b} .
Then R1 = R2 if and only if a = 1 and
b = 2.
![]() A1
A1
![]() ...
...
![]() An
and
an m-ary relation
R2
An
and
an m-ary relation
R2
![]() B1
B1
![]() ...
...
![]() Bm
are equal
if and only if m = n, Ai = Bi
for each i,
1
Bm
are equal
if and only if m = n, Ai = Bi
for each i,
1
![]() i
i
![]() n , and
R1 = R2 as a set of ordered n-tuples.
n , and
R1 = R2 as a set of ordered n-tuples.