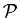Zermelo-Fraenkel Set Theory

Zermelo-Fraenkel set theory is a theory based on the firstl order predicate logic. The members of its universe of discourse are sets, which are characterized by the axioms given below. There is a binary relation between members of the universe, set membership: set a is a member of set b written as a ∈ b. Following are the axioms of Zermelo-Fraenkel. They together characterize 'sets'. Except the regularity axiom they are basically the same assumpotions that are made in the naive set theory. The regularity axiom is the one that eliminates inconsistencies found in the naive set theory such as Russell's paradox.

A reader with familiarity with the first order logic should have no trouble in understanding the follwoing presentation.

Axioms of ZF

Extensionality:

∀x∀y[∀z[z∈x ↔ z∈y] → x=y]

This axiom states that two sets are equal when they have the same members.

Null Set:

∃x~∃y[y ∈ x]

This axiom asserts the existence of the null (empty) set.
It can be proven from this axiom and the previous axiom that such a set is unique. We denote it by φ.

Pairs:

∀x∀y∃z∀w[w∈z ↔ [w=x ∨ w=y]]

This axiom states that given any sets x and y, there exists a set which has only x and y as its members.
It can be proven that there is a unique such set for each given x and y. We call it a pair (set) and denote it by {x,y}.

Unions:

∀x∃y∀z[z∈y ↔ ∃w[w∈x ∧ z∈w]]

This axiom states that for any given set x, there is a set y which has as its members all of the members of all of the members of x. Such a set y is called a union of x. It can be proven that there is a unique union of any set x. We denote it by ∪x.

For excample let x = {{1,2}, {3}, {4}, {5,6,7}}. Then y = ∪x = {1,2,3,4,5,6,7}.

For any sets x and y, we write ∪ { x, y} also as x ∪ y. Note that this is the union of two sets x and y as known from the naive set theory.

For any set x, a set y is called a subset of x if every member of y is a member of x. We write y ⊆ x to denote that y is a subset of x.

The next axiom states that for any set x, there is a set y which contains as its members every set whose members are also elements of x, i.e., y contains all of the subsets of x. Such a set y is called a power set of x.

Power Set:

∀x∃y∀z[z∈y ↔ ∀w[w∈z → w∈x)]

It can be proven that a set has a unique power set. We denote the power set of a set x by 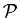(x).

The next axiom asserts the existence of an infinite set, i.e., a set with an infinite number of members:

Infinity:
∃x[φ ∈ x ∧ ∀ y[y ∈ x → ∪{y,{y}}∈ x]], where φ denotes the empty set.

The Axiom of Infinity asserts that there is a set x which contains φ as a member and that anytime y is a member of x, y ∪ {y} is also a member of x. Thus, this axiom guarantees the existence of a set of the following form:

{φ, {φ}, {φ, {φ}}, {φ, {φ}, {φ, {φ}}}, ... }

The next axiom puts some restriction on the kind of members a set can have. It eliminates the Russell's paradox among others.

Regularity:
∀x[x ≠ φ → ∃ y[y ∈ x ∧ ∀ z[z ∈ x → ~z∈y]]]

This axiom asserts that every non-empty set x contains an element y which is disjoint from x. Thus it rules out among the sets the existence of x such that x = {x}. Infinitely descending chains of sets such as ... x2 ∈ x1 ∈ x0 are not allowed either.

The final axiom of ZF is the Replacement Schema. Suppose that P(x,y) is a wff (well formed formula) with x and y free, and which may or may not have other free variables. Also, let P(s,r) be the result of substituting s and r for x and y, respectively, in P(x,y). Then every instance of the following wff is an axiom:

Replacement Schema:
∀x∃!y[P(x,y → ∀u∃v∀r[r∈v ↔ ∃s[s∈u ∧ P(s,r)]]]

In English it states the following: Suppose that P(x,y) is a formula which relates each set x to a unique set y. Then given a set u, we can form a new set v (hence such a set exists) by collecting all of the sets to which the members of u are uniquely related by P.

It is called a schema because it collectively represents infinite number of axioms of the same form.