1 Storage Models

When a program is executing, its memory space will be divided into three areas:

• The static storage area is a fixed size that does not change from the moment the program starts running until the program halts.
• The heap is variable size and grows based upon explicit commands from the running program.
• The call stack (a.k.a. activation stack) grows with each function call and shrinks upon return from a function.

The heap and the call stack grow toward each other. This allows us to make the most efficient use of the unused portion fo the address space. One program might have a huge call stack and little to no heap. Another might have a small stack and a massive heap. Others might be more balanced. As long as the heap and the call stack don’t actually collide, we still have address space left to grow in.

The real situation is slightly more complicated than that. Modern operating systems use virtual memory to map however much RAM memory is actually installed onto a much larger range of possible addresses, so we can run out of memory long before the heap and the call stack actually meet. But the essential thing to realize is that the two areas can never share the same block of addresses.

The storage area that a variable or value resides in will determine its lifetime, the period of time within which that value can be accessed. Before its lifetime, a value might not be initialized to anything meaningful. After its lifetime, the block of memory occupied by that variable might be reused for some other purpose, leading to the value being overwritten by some other data.

1.1 Automatic Storage

The call stack area manages the data associated with functions.

• When a function is called, a block of data called an activation record is pushed onto the stack.
• When we return from that function, that block of data is popped or removed from the stack.

The activation record for a function call records various housekeeping information necessary to manage the call and return mechanisms. From the perspective of this lesson, however, the most important thing contained in the activations records is the storage space for all variables local to that function’s body.

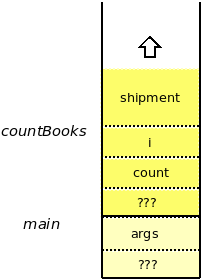
Consider the following program:

public class Shipment {
  public int numBooks;
  public int numMagazines;
}

Shipment[] received = new Shipment[100];
int numShipments = 0;

void readShipments() // fills in received and numShipments
{
  ⋮
}

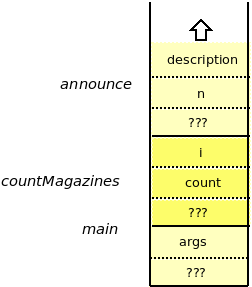
void announce (int n, string description)
{
  System.out.println("We have received " + n + " " + description);
}

void countBooks()
{
  int count = 0;
  for (int i = 0; i < numShipments; ++i)
  {
    Shipment shipment = shipments[i];
    count += shipment.numBooks;
  }
  announce (count, "books");
}

void countMagazines()
{
  int count = 0;
  for (int i = 0; i < numShipments; ++i)
  {
    count += shipments[i].numMagazines;
  }
  announce (count, "magazines");
}


int main(String[] args)
{
  readShipments();
  countBooks();
  countMagazines();
}

If we trace what happens in this program, while watching the call stack, we can see how storage space for most of the variables appears and disappears.

 

The program starts by calling main. An activation record for main is pushed onto the stack. There will be a certain amount of bookkeeping information in there (designated as “???”) and space to hold the parameter args.

 

main calls readShipments. An activation record for readShipments is pushed onto the stack. We have not shown the code for this, so there’s no telling what else might be in the new activation record.

 

readShipments finishes up and returns to main. The activation record for readShipments is popped from the stack.

 

main now calls countBooks. The activation record for countBooks is pushed onto the stack, with enough room for the local variables count and i.

 

countBooks eventually enters the loop body. When it does so, storage space for shipment is pushed onto the stack.

 

When execution reaches the end of the loop body, the storage space for shipment is popped from the stack.

 

But when we repeat the loop body for the second time, storage space for shipment is pushed onto the stack…

 

… and then popped again at the end of the loop body.

In theory, this push/pop sequence continues for as many times as the loop repeats. In practice, C++ compilers will usually preallocate the space for shipment in the activation record upon entering the function. But some languages and compilers do actually push and pop the storage each time you enter and leave {...} sections that contain a local variable. And C++ behaves as if it were creating and removing the storage for that variable:

• If Shipment had a constructor, it would be invoked to re-initialize shipment each time we enter the loop body.
• And if Shipment had a destructor, it would be invoked to clean up shipment each time we hit the end of the loop body.

 

Eventually, countBooks will exit its loop and will call announce. A new activation record is added to the stack, with storage space for its parameters.

 

announce does its thing, and then returns to its caller.

 

countBooks is now finished, to it returns to its caller.

 

main then calls countMagazines.

 

countMagazines runs through its loop and eventually calls announce.

 

announce does its thing, and then returns to its caller.

 

countMagazines is done, and returns to its caller.

main is now done. When it returns, the program is shut down.

1 of 15

So, the thing to observe from all this is that storage for parameters and local variables appears just when we need it, upon entering a function call, and disappears when it is no longer needed, upon return from the function.

The programmer doesn’t need to issue any explicit instructions at all to make this happen. Consequently, variables like this are said to have automatic storage.

1.2 Static Storage

Static storage holds data values whose lifetime starts and ends when the entire program starts and ends.

In Java, these are primarily system variables tht we would not have direct access to.

1.3 Dynamic Storage

The heap area is for data that is allocated by explicit programmer instructions. In Java these instructions take the form of uses of the new operator. The new operator returns a pointer to the newly allocated block of data. E.g.,

Shipment aShipment = new Shipment();

1.3.1 How Data Gets Deleted

In C++ and many other languages, data that is allocated in the heap will remain there until another explicit programer instruction, the delete operator, is invoked on that pointer. Deleting a pointer returns the pointed-to block of data to the operating system.

In Java and Python, programmers do not explicitly delete blocks of data. Instead, process called the garbage collector runs in the background looking for “garbage” on the heap, blocks of data that can no longer be reached from data in the static area or in the activation stack. Where it finds such garbage blocks, it deletes them.

1.3.2 Reusing Deleted Storage

The operating system keeps track of the blocks of memory that have been deleted in a free list.

• When a block of memory is deleted, it is added to the current free list. This action may involve writing some data into the block of memory, overwriting part of the data that used to be stored there.
• When a later new request is made, the request will specify how many bytes are needed.

  The operating system will first check to see if there is a block of memory on the free list that is large enough to accommodate the new request.

  • If so, it removes that block from the free list and hands its address back to the new request.
  • If not, then the operating system expands the heap by the required number of bytes, and gives to the new request the address of the new addition to the heap.

  So, whenever possible, new will reuse previously deleted blocks of memory. If that is not possible, the heap is expanded.

2 Low-level Storage Management

If you were to examine the operating system code for allocating new blocks of memory and deleting previously allocated ones, you would find that they maintain a free list of blocks of deleted memory.

• This is somewhat more complicated than the free lists discussed i nthe text because the blocks are of highly varying sizes.

Suppose a program repeatedly allocates and deletes objects of varying sizes on the heap (e.g., strings):

{
    String z = new String("Zeil");
    String a = new String("Adams");
    String j = new String("Jones");
}

The operating system maintains a free list of unallocated blocks of memory on the heap.

If we later do

delete a;

in C++ or just

a = null;

in Java and then wait for the Garbage Collector to notice,

then the block of memory of “Adams” is added to the freelist.

The blocks of memory don’t actually move around. They are just managed using linked list nodes that point to the freed blocks of memory.

That was a bit of an oversimplification.

What usually happens is that the opening bytes of each freed block of memory is overwritten by the pointer to the next block in the free list, making it unnecessary to actually maintain a separate list.

2.1 Fragmentation

A new allocation request, e.g.,

String t = new String("ABC");

requires the OS (or the Java VM) to search the free list for a block of appropriate size.

2.1.1 Searching the free list

2.1.2 Searching the free list

• Common schemes for such a search are

  • first fit — choose the first block in the free list that is big enough

  • best fit — choose the block in the free list that is closest to the requested size from among those that are no smaller than the requested size.

If a block is “big enough” but is larger than we need, what do we do with the rest of the block?

2.1.3 Dealing with Inexact size matches

Two options:

• Return the whole over-sized block

  • Safe, but wastes memory.

• Or, split oversized blocks

  • Break off part that is just large enough to satisfy the request.
  • The remainder is placed back on the free list.

    Over time, a program that does many allocations and deletes may find more and more storage wasted on small fragments left on the free list, too small to be useful.

    This is called fragmentation. This is called fragmentation.

2.2 Performance

2.3 Performance

• Free list length could be $O(k)$ where $k$ is the total number of deletes.

• Since each new requires a search of that list, new becomes $O(k)$.

  • instead of $O(1)$, as usually assumed

• Deleting a block is $O(1)$.

This explains why, on occasion, you will find a program that has been running for a long time seems to be getting slower and slower. The free list is being choked with small fragments, so new allocation requests are taking longer and longer.

If such a program is run long enough, it may crash when an allocation request can no longer be satisfied, even though there is more than enough free memory in total.

2.3.1 Compaction

Some systems try to reduce or eliminate fragmentation:

• One way is to use compaction: As regions are freed, sort them by address so that adjacent regions of memory are also adjacent within the free list.

  • Adjacent free regions can then be merged to form a single, larger region.

  • Now deleting is worst case $O(k)$.

  • but $k$ might be smaller

2.3.2 Uniformly-sized Pools

• Another idea: only allocate regions in selected sizes: 1, 2, 4, 8, 16, 32, 64, …

  • E.g., If a request is made for 10 elements, a 16-element regions is actually returned.

  • A separate free list is kept for each size of region.

  • Larger regions can be split in half to form two smaller regions, when necessary.

  • new and delete remain O(1)

    • but storage utilization may suffer – on average wastes 25% of memory

Even with all this, you can see why sometimes we would prefer to handle our own storage management. Implementing our own freelist let’s us do allocation and freeing of memory in O(1) time, because all of the data objects on our own freelist will be of uniform size. The more general problem of allocating and freeing memory of different data types of many varying sizes is much harder, and will either have a complexity proportional to the number of prior deletions, or will waste a substantial fraction of all memory.