1 Basic Manipulation

We start with a pair of simple, almost self-evident rules:

Algebraic Rule 1: $f(\bar{n}) + g(\bar{n}) \in O(f(\bar{n}) + g(\bar{n}))$

This rule comes into play most often when we discover that a program has to do two (or more) things before it is finished, one of which takes time $f(\bar{n})$ and the other takes time $g(\bar{n})$. The rule simply says that the running time of the entire program might be no faster than the sum of the running times of its constituent parts.

Because this is only an upper bound, the program might actually be faster than that (e.g., if the first part of the program prepares the data in some fashion that allows the second part to run faster than it would have in isolation). But it will be no slower, in the worst case, than some constant times the sum of the two run time bounds.

Algebraic Rule 2: $f(\bar{n}) * g(\bar{n}) \in O(f(\bar{n}) * g(\bar{n}))$

This rule comes into play most often when we discover that a program has a loop that runs through $f(\bar{n})$ iterations, and each iteration of the loop takes $O(g(\bar{n}))$ time. Then the program will be no slower, in the worst case, than some constant times the product of those two functions.

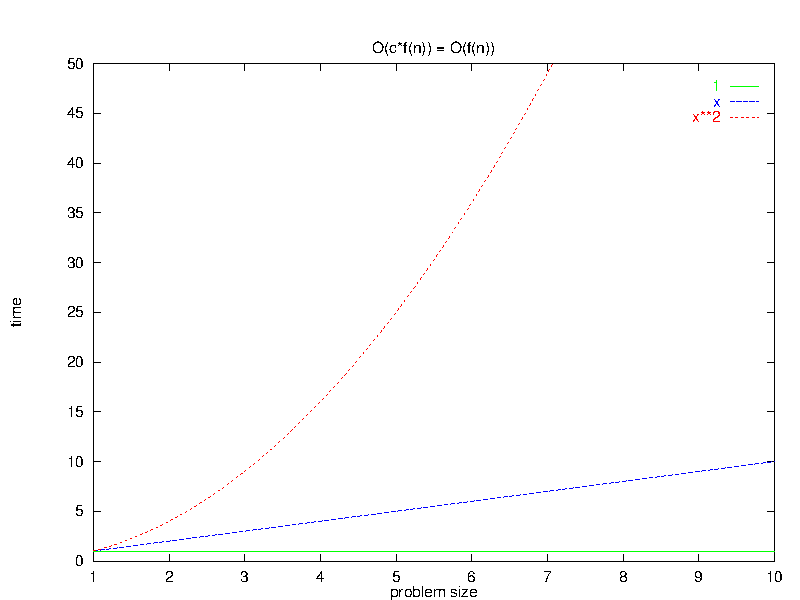
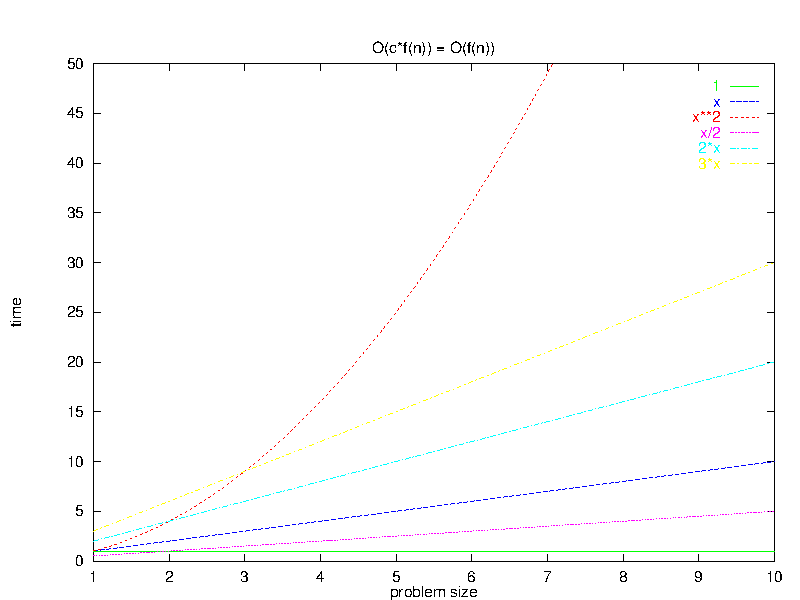
2 Dropping Constant Multipliers

Our next rule is a bit less intuitive:

Algebraic Rule 3:

$O(c*f(\bar{n})) = O(f(\bar{n}))$

This rule suggests that, for sufficiently large $\bar{n}$, constant multipliers “don’t count”.

2.1 Intuitive Justification

 

To see why this might be so, suppose we have three programs that run in time $O(1)$, $O(x)$, and $O(x^{2})$, where $x$ is the size of the input set.

Notice from the plot of these three times, that, for sufficiently large $x$, the $O(x)$ time falls between the other two.

 

Now add some more programs, whose running times differ from the $O(x)$ program only by constant multipliers.

• Note that the new $O(c*x)$ programs all run faster than the $O(x^{2})$ program (for sufficiently large $x$).

  • Note especially that, as $x$ gets bigger, the differences between the $O(x^{2})$ program and any of the $O(c*x)$ programs is far, far bigger than the differences among the $O(c*x)$ programs.

  • This suggests that knowing whether the “main” function is $x$ or $x^{2}$ is far more important than knowing what $c$ is.

 

• Note, similarly, that the $O(c*x)$ programs all run slower than the $O(1)$ program.

  • And again, note that, as $x$ gets bigger, the differences between the $O(1)$ program and any of the $O(c*x)$ programs is far, far bigger than the differences among the $O(c*x)$ programs.

  • Again, this suggests that knowing whether the “main” function is $x$ or $1$ is far more important than knowing what $c$ is.

 

We can see a similar pattern with even larger functions.

Suppose we start with three programs that run in time $O(x)$, $O(x^{2})$, and $O(x^{3})$, where $x$ is the size of the input set.

Notice from the plot of these three times, that, for sufficiently large $x$, the $O(x^{2})$ time falls between the other two.

 

Now add some more programs, whose running times differ from the $O(x^{2})$ program only by constant multipliers.

• Note that the new $O(c*x^{2})$ programs all run faster than the $O(x^{3})$ program (for sufficiently large $x$).

  • Note especially that, as $x$ gets bigger, the differences between the $O(x^{3})$ program and any of the $O(c*x^{2})$ programs is far, far bigger than the differences among the $O(c*x^{2})$ programs.

  • This suggests that knowing whether the “main” function is $x^{2}$ or $x^{3}$ is far more important than knowing what $c$ is.

 

• Note, similarly, that the $O(c*x^{2})$ programs all run slower than the $O(x)$ program.

  • And again, note that, as $x$ gets bigger, the differences between the $O(x)$ program and any of the $O(c*x^{2})$ programs is far, far bigger than the differences among the $O(c*x^{2})$ programs.

  • Again, this suggests that knowing whether the “main” function is $x^{2}$ or $x$ is far more important than knowing what $c$ is.

1 of 6

2.1.1 So What Good are Constants?

Does this mean that constant multipliers aren’t relevant at all?

• No. Suppose we had two programs A and B with times \[ t_{A} (N) = N * (1 second) \] \[ t_{B} (N) = N * (1 minute) \]

  • For $N=60$, this is the difference between waiting 1 minute and waiting for 1 hour. No one will argue that this difference is insignificant.

• But now suppose that we consider a third program C with an even smaller constant:

  \[ t_{C} (N) = N^{2} * (0.01 second) \]

  Even though this program has a much smaller constant factor, and will perform much faster on small $N$, it will be slower than program $A$ whenever $N > 100$ and slower than $B$ when $N > 6000$.

• So the constant can play a role in choosing the faster algorithm only when the function parts of the complexity are equal.

2.2 Proof: $O(c*f(\bar{n})) = O(f(\bar{n}))$

All we have done so far is to give examples that this rule holds. No number of examples can constitute a proof. To prove that it holds in general, consider any program with running time $t(\bar{n}) = O(c*f(\bar{n}))$.

By the definition of $O(\ldots )$, we have:

\[ \exists c_1, \bar{n}_0 | \bar{n} > \bar{n}_0 \Rightarrow t(\bar{n}) \leq c_1 (c * f(\bar{n})) \]

But, grouping the multiplication slightly differently gives

\[ \exists c_1, \bar{n}_0 | \bar{n} > \bar{n}_0 \Rightarrow t(\bar{n}) \leq (c_1 * c) f(\bar{n}) \]

Now, since $c$ and $c_{1}$ are both constants, we can introduce a new constant $c_{2}$:

\[ c_{2} = c_{1} * c \]

and then we can claim that

\[ \exists c_1, \bar{n}_0 | \bar{n} > \bar{n}_0 \Rightarrow t(\bar{n}) \leq c_2 * f(\bar{n}) \]

But this is just the definition of $O(f(\bar{n}))$, so we conclude that

\[ t(\bar{n})=O(f(\bar{n})) \]

Therefore any program in $O(c*f(\bar{n}))$ is also in $O(f(\bar{n}))$.

It’s easy enough to modify the above argument to show that any program in $O(f(\bar{n}))$ is also in $O(c*f(\bar{n}))$ (e.g., replace $c$ by $1/c$).

So the sets $O(f(N))$ and $O(c*f(N))$ are, in fact, the same.

Q.E.D.

This rule can be applied across sums, by the way. If we have two functions f(N) and g(N) and two constants $c_1$ and $c_2$, then it’s easy to modify the above proof to show that

\[O(c_1*f(\bar{n}) + c_2*f(\bar{n})) = O(f(\bar{n}) + g(\bar{n}))\]

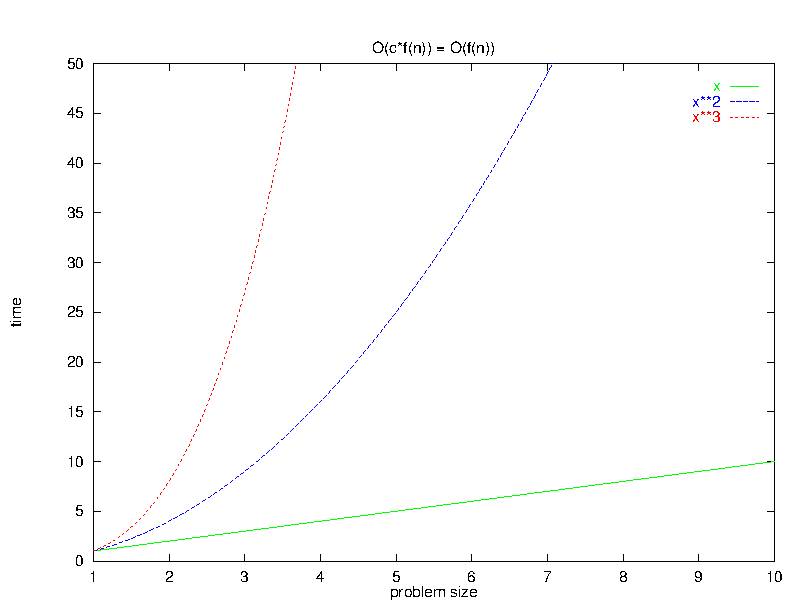
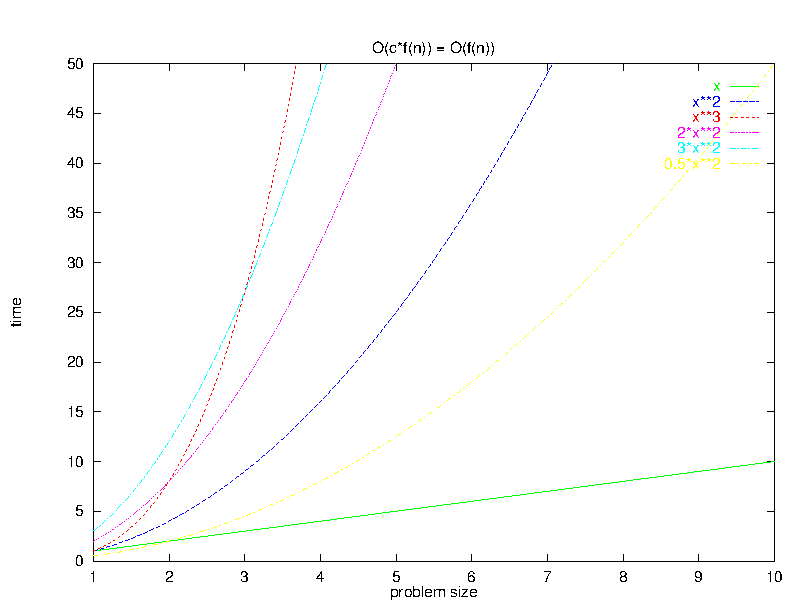
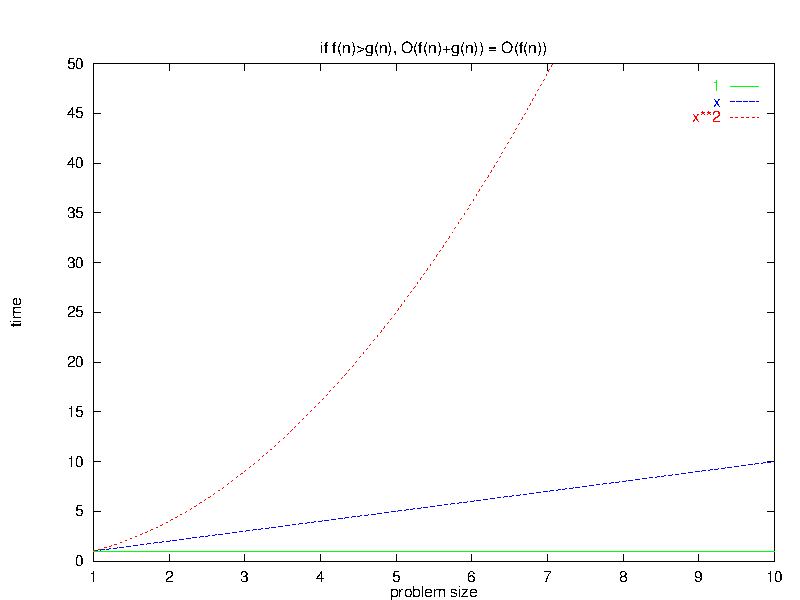
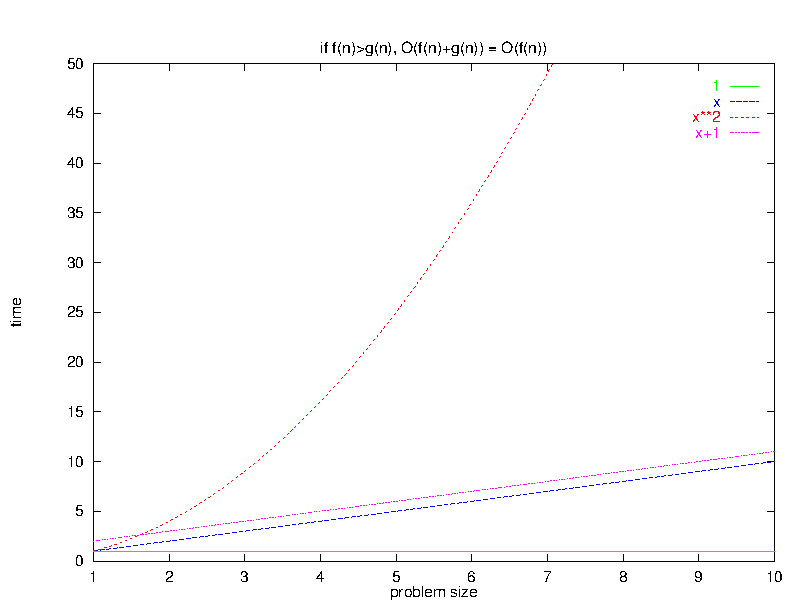
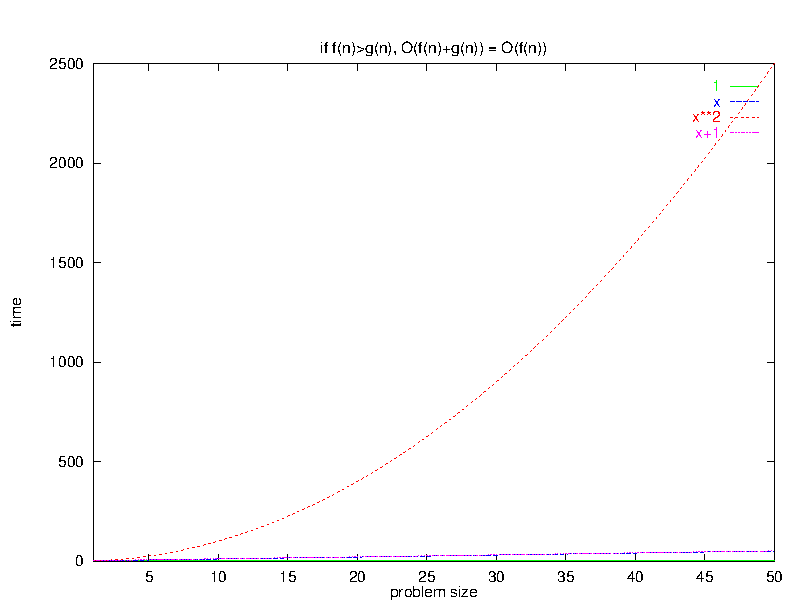
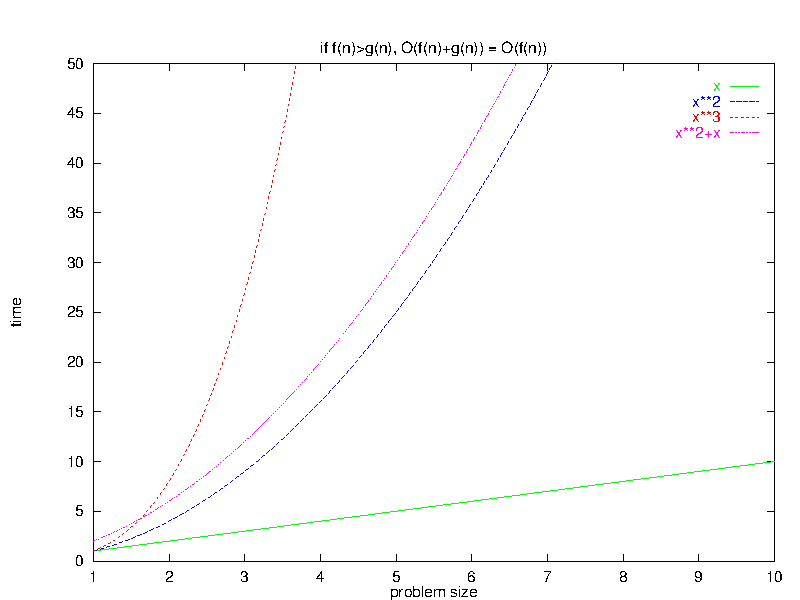
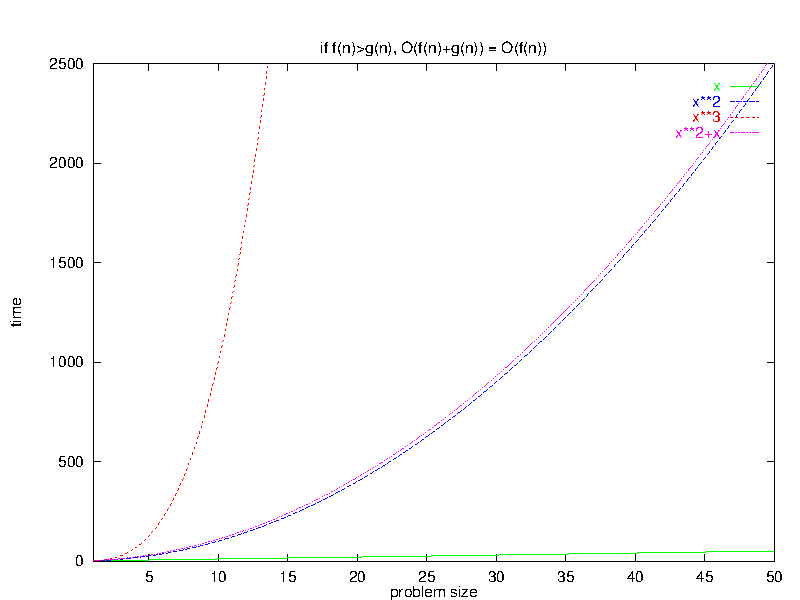
3 Larger Terms Dominate a Sum

Algebraic Rule 4:If $\exists \bar{n}_0 \; | \; \forall \bar{n} > \bar{n}_0, \, f(\bar{n}) \geq g(\bar{n})$, then $O(f(\bar{n}) + g(\bar{n})) = O(f(\bar{n}))$

This rule states that, if we have a program that does two different things before it finishes, then for large input sets the slower of these two will dominate the overall time.

3.1 Intuitive Justification

 

To see why this might be so, suppose we have three programs that run in time $O(1)$, $O(x)$, and $O(x^{2})$, where $x$ is the size of the input set.

As before, we note that, for sufficiently large $x$, the $O(x)$ time falls between the other two.

 

Now we add another program, that does the same work as the $O(x)$ program plus some additional $O(1)$ work, for a total of $O(x + 1)$.

• Note that the new $O(x+1)$ program still runs faster than the $O(x^{2})$ program and slower than the $O(1)$ program (for sufficiently large $x$).

 

• In fact, if we “pull back” our perspective and look at a larger range of input sizes, we see that the difference between the $O(x)$ and $O(x+1)$ programs virtually disappears. (Depending upon your browser settings, you may not even be able to tell the two lines apart.)

We can show that this same effect holds for even larger functions.

 

Suppose we start with three programs that run in time $O(x)$, $O(x^{2})$, and $O(x^{3})$, where $x$ is the size of the input set.

Notice from the plot of these three times, that, for sufficiently large $x$, the $O(x^{2})$ time falls between the other two.

 

Now add another program that runs in time $O(x^{2} + x)$.

• Note that the new $O(x^{2} + x)$ program runs faster than the $O(x^{3})$ program and slower than the $O(x)$ program (for sufficiently large $x$).

 

And, again, if we pull back our perspective to consider even larger input set sizes we again see that the difference between the $O(x^{2})$ and $O(x^{2}+x)$ programs virtually disappears.

1 of 6

In essence, adding a “lower-order” function (e.g., $x$) to a “higher-order” one (e.g., $x^{2}$) does not sufficiently alter the curvature of the new higher-order function enough to change its big-O relationship to other even higher- (e.g., $x^{3}$) and lower-order (e.g., $x$) functions.

3.2 Proof: Larger Terms Dominate a Sum

To prove that, if $\forall \bar{n} > \bar{n}_0. f(\bar{n}) \geq g(\bar{n})$, then $O(f(\bar{n}) + g(\bar{n})) = O(f(\bar{n})),$ consider any program with running time $t(\bar{n}) = O(f(\bar{n}) + g(\bar{n}))$.

By the definition of big-O, we know that, for some $c$ and $\bar{n}_1$, we have:

\[ \bar{n} > \bar{n}_1 \Rightarrow t(\bar{n}) \leq c (f(\bar{n}) + g(\bar{n})) \]

But assume that $\forall \bar{n} >{} 0, f(\bar{n}) \geq g(\bar{n})$

Then we can claim that the following are also true:

\[ \begin{align} \bar{n} > \max(\bar{n}_0, \bar{n}_1) & \Rightarrow t(\bar{n}) \leq c (f(\bar{n}) + g(\bar{n}) ) \;\;\; & (1)\\ \bar{n} > \max(\bar{n}_0, \bar{n}_1) & \Rightarrow f(\bar{n}) > g(\bar{n}) & (2) \end{align} \]

But equation (2) suggests that we can, for those values of $\bar{n}$, replace the $g(\bar{n})$ by $f(\bar{n})$ in equation (1) and, because we are replacing one quantity by an even larger one, the “$\leq$” relation will still hold:

\[ \begin{eqnarray} \bar{n} > \max(\bar{n}_0, \bar{n}_1) & \Rightarrow & t(\bar{n}) \leq c (f(\bar{n}) + f(\bar{n})) \\ \bar{n} > \max(\bar{n}_0, \bar{n}_1) & \Rightarrow & t(\bar{n}) \leq 2c * f(\bar{n}) \end{eqnarray} \]

But $2c$ and $max(\bar{n}_{0}, \bar{n}_{1})$ are just constants, so that final
equation simply expresses the big-O definition: $t(\bar{n}) = O(f(\bar{n}))$

Q.E.D.

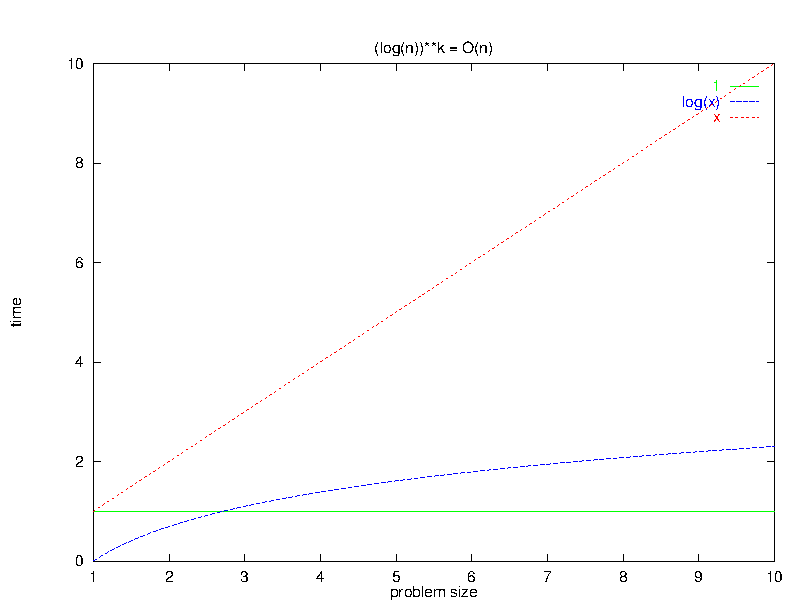
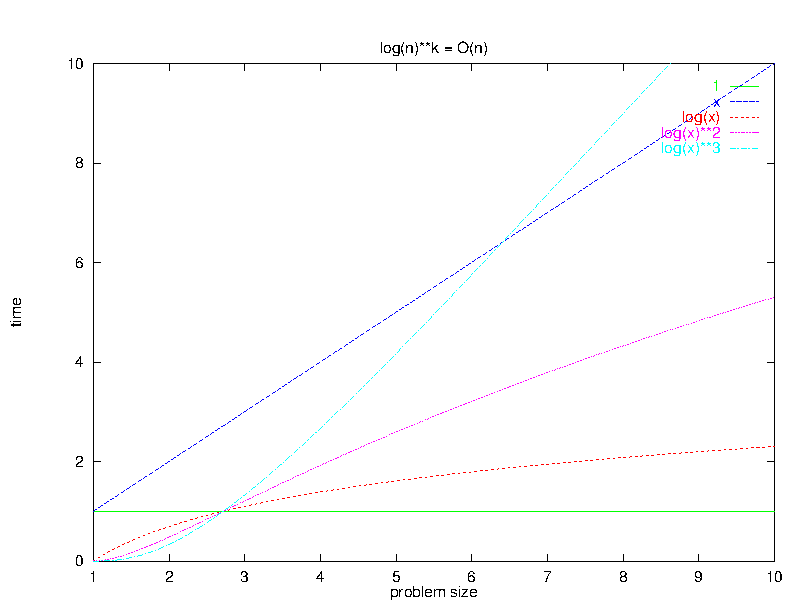
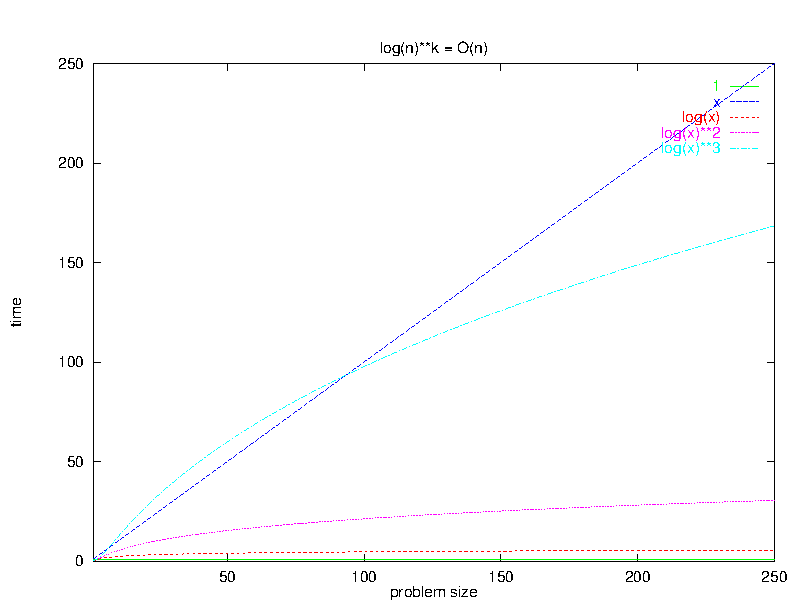
4 Logarithms are Fast

Our final rule doesn’t come into play as often as the others, but is still useful on occasion:

Algebraic Rule 5: $\forall k \geq 0, O(\log^{k}(n)) \subset O(n)$

5 Summary of big-O Algebra

The five rules we have presented:

1. $f(\bar{n}) + g(\bar{n}) \in O(f(\bar{n}) + g(\bar{n}))$

2. $f(\bar{n}) * g(\bar{n}) \in O(f(\bar{n}) * g(\bar{n}))$

3. $O(c*f(\bar{n})) = O(f(\bar{n}))$

4. If $\exists n_0 | \forall \bar{n} > n_0, f(\bar{n}) \geq g(\bar{n})$, then $O(f(\bar{n}) + g(\bar{n})) = O(f(\bar{n}))$

5. $\forall k \geq 0, O(\log^{k}(n)) \subset O(n)$

allow us to simplify complicated analyses without resorting to a full-blown proof based upon the definition of big-O.

For example, we earlier looked at a piece of code that we felt ran in time

\[ \begin{eqnarray*} t(N) & = & N^{2} (2t_{\mbox{asst}} + t_{\mbox{comp}} + 4t_{\mbox{add}} + 3t_{\mbox{mult}}) \\ & & + N (3t_{\mbox{asst}} + 2t_{\mbox{comp}} + 2t_{\mbox{add}} + t_{\mbox{mult}}) \\ & & + 1 (t_{\mbox{asst}} + t_{\mbox{comp}}) \end{eqnarray*} \]

Since this is the exact running time, it is also an upper bound. Therefore,

\[ \begin{eqnarray*} t(N) & \in & O(N^{2} (2t_{\mbox{asst}} + t_{\mbox{comp}} + 4t_{\mbox{add}} + 3t_{\mbox{mult}}) \\ & & + N (3t_{\mbox{asst}} + 2t_{\mbox{comp}} + 2t_{\mbox{add}} + t_{\mbox{mult}}) \\ & & + 1 (t_{\mbox{asst}} + t_{\mbox{comp}})) \end{eqnarray*} \]

By rule 4, the higher-order $N^{2}$ term will dominate this sum:

\[ t(N) \in O(N^{2} (2t_{\mbox{asst}} + t_{\mbox{comp}} + 4t_{\mbox{add}} + 3t_{\mbox{mult}}))\]

By rule 3, we can discard the constant multipliers:

\[ t(N) \in O(N^{2}) \]

This is, I hope you’ll agree, much simpler than the proof we engaged in when we first analyzed that code.

5.1 The Tao of N

Finally, keep in mind that $n$ or $N$ is merely a placeholder here for what may be an expression involving multiple measures of the input set size. Only the last of these rules is limited to a single variable (because the expression “$\log(n)$” only makes sense if $n$ is a single quantity, although it can still be any single expression, e.g., $\log(n^{3} + 1/n)$.

For example, if we were presented with a function that was $O(30.0 x^{2} + 15.0 y + 2 x)$, we could simplify it as follows:

\[\begin{align*} O(30.0 x^{2} + 15.0 y + 2 x) & \\ & = O(30.0 x^{2} + 15.0y) & \mbox{(by rule 4)} \\ & = O(x^{2} + y) & \mbox{(by rule 3)} \end{align*}\]

and would have to stop there. Although $x^{2}$ has a larger exponent than $y$, we can’t assume that it dominates $y$ unless we have some other information about the relative sizes of $x$ and $y$.

If someone were to come by later and inform us, “Oh, by the way, it’s always true that $y \leq x$”, then we could indeed simplify the above to $O(x^{2})$. On the other hand, if that same mysterious font of information were to instead say, “Oops, my mistake. Actually $y \geq x^{3}$”, then we would simplify $O(x^{2} + y)$ to $O(y)$.

6 Always Simplify!

Whenever you analyze an algorithm in an assignment, quiz or exam in this course, you should employ these algebraic rules to present your answer in the simplest form possible. If you don’t, your answer will be considered wrong!