1 A Diversion - Function Calls at the Machine Level

In a sense, all recursion is an illusion. At the machine level, you have an iterative process for fetchign and executing instructions. All function calls (including the recursive ones) are implemented via a runtime stack (called the activation stack) to keep track of the return addresses, actual parameters, and local variables associated with function calls. Each function call actually results in pushing an activation record containing that information onto the stack. Returning from a function is accomplished by getting and saving the return address out of the top record on the stack, popping the stack once, and jumping to the saved address.

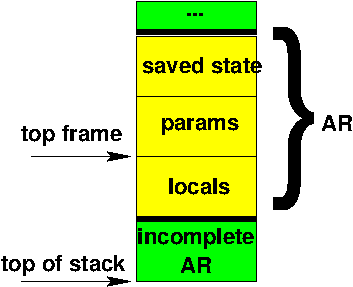
The actual structure of activation stacks is machine and compiler dependent. A typical one is shown here.

Typical contents of the saved state area would include

• the return address - where to go when returning from the call, and

• contents of critical machine registers at the start of the call

Contents of the params area would be

• the values fo the actual parameters being passed to the function

• space for the return value that the call will eventually send back to the caller

The locals area holds the space for any local variables declared within the called function’s body.

The collection of all this information for a single call is called an activation record or, sometimes, a frame. An activation stack is typically managed via two pointers. One is the true top of the stack. The other is a pointer to the top completed frame or activation record - the one describing the function that is currently being executed. These two pointers are often slightly different. That’s because, if the currently executing function is getting ready to call some other function, it will get ready by pushing its saved state info and any parameterts it wants to pass onto the top of the stack, forming an “incomplete” actication record as shown in the diagram.

For a function call foo(a, b+c, d);, the caller would

• Push state information, including a return address and the current values of the top-of-stack and top-frame pointers.

• Evaluate each of the three parameter expressions, pushing their values onto the stack. If foo has a non-void return type, the caller would also push enough space for the return value.

• The caller would then jump to the starting address of foo’s function body.

The code in the body of foo would typically start by pushing enough additional bytes onto the top of the stack to allow room for all of the local variables declared in that function body. This completes the activation record for the call to foo.

The execution fo the function body of foo then proceeds. When a return statement (or end of the body) is encountered,

• the return value (if any) is written into the spoace reserved for it in the params area

• a jump is made to the return address recorded in the saved state area

Upon return to the original caller, the caller then

• copies the return value (if any) to some appropiate location

• restores to top frame and top-of-stack pointers to their saved values. In effect, this pops the entire activation record that had been built for foo off of the stack, leaving the caller’s activation record back on top.

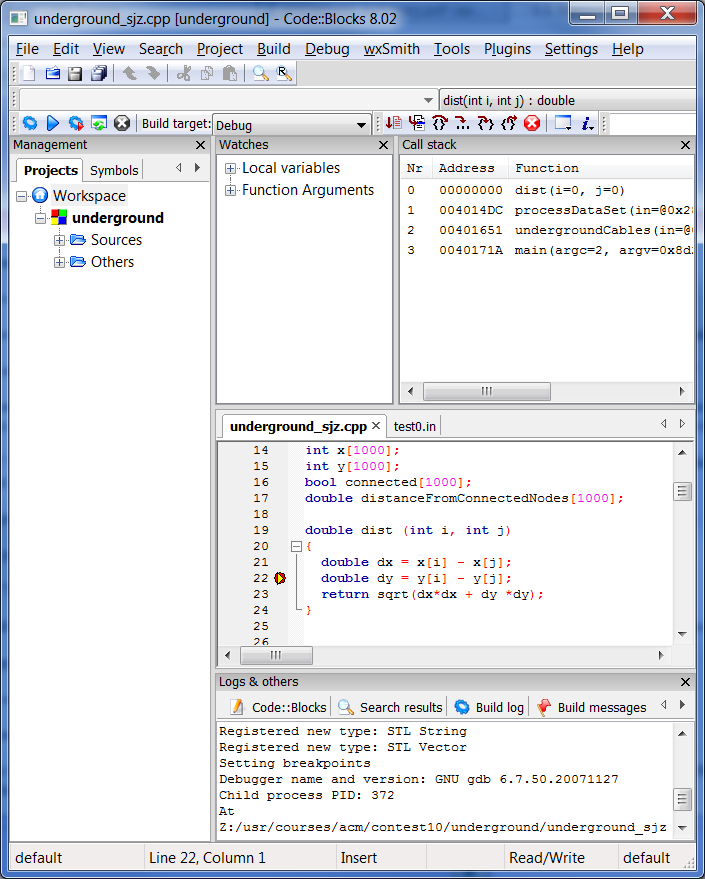
You can observe activation stacks in almost any debugger. Set a breakpoint and execute the code until that breakpoint is reached. When execution pauses, most debuggers will show not only where you stopped, but how you got there (in the form of the activation stack). In the picture shown here, for example, you can see that we have reached a breakpoint inside a function called dist, In the upper right corner, however you can see the entire activation (call) stack at this point in time. Like all C++ programs, we started by running main. In this program, main called undergroundCables, which called processDataSet, which called dist.

This stack-based approach to execution handles recursive calls naturally. A recursive call is just one that happens to put another activation record for the same function body onto the stack. But that really makes no difference at all in how the machine-level execution treats that call. Arguably, the only difference is what happens when things go wrong. If you have an iterative algorithm and you make a mistake that leads to an infinite loop, the program simply runs forever (or until you kill the program). With a recursive algorithm, if you mess up and get into an infinte recursion, the program runs for a while and then crashes due to a lack of memory. An infinite recursion causes the activation stack to grow longer and longer until it occupies all available memory.

In a sense, then, computers really don’t do recursion. What we might write as a recursive algorithm really gets translated as a series of stack pushes followed by a jump back to the beginning of the recursive function, all implemented using the underlying CPU whose internal code is, fundamentally, iterative. With that in mind, you can see why, if we wanted to rewrite our own code to eliminate recursion, stacks are likely to prove useful.

2 Converting Recursive Algorithms to Iteration

How, then do we go about converting recursive functions to an iterative form?

2.1 Tail Recursion

A function is called \first-term{tail-recursive} if each activation of the function will make at most a single recursive call, and will return immediately after that call (with no further calculation performed upon the return value from the call).

Tail recursive routines have an immediate, and simple pattern of conversion.

T tailRecursiveFoo(U x, V y)
{
  if (bar(x, y))
    return baz(x,y);
  else
    {
     ⋮ // block 1
     return tailRecursiveFoo(w, z);
    }
}

becomes

T Foo(U x, V y)
{
  while (! bar(x, y))
    {
      ⋮ // block 1
      x = w;
      y = z;
    }    
  return baz(x,y);
}

2.1.1 Tail Recursion Example: binarySearch

An example of tail-recursion is the binary search, which converts by the pattern just shown from the recursive form shown here:

unsigned int binarySearch 
  (T v[], unsigned int n, const T& value)
    // search for value in ordered array of data
    // return index of value, or index of
    // next smaller value if not in collection
{
  binarySearch (v, 0, n, value);
}

unsigned int binarySearch 
  (T v[], unsigned int low, int high, const T& value)
{
  // repeatedly reduce the area of search
  // until it is just one value
  if (low < high) {
     int mid = (low + high) / 2; 
     if (v[mid] < value)
         {
           return binarySearch (v, mid + 1, high, value);
         }
     else
         {
           return binarySearch (v, low, mid, value);
         }
     }
  else
     // return the lower value
     return low;
}

into its more familiar iterative form:

unsigned int binarySearch 
  (T v[], unsigned int n, const T& value)
    // search for value in ordered array of data
    // return index of value, or index of
    // next smaller value if not in collection
{

  int low = 0;
  int high = n;

  // repeatedly reduce the area of search
  // until it is just one value
  while (low < high) {
     int mid = (low + high) / 2; 
     if (v[mid] < value)
         {
             low = mid + 1;  
         }
     else
         {
             high = mid;  
         }
     }
  // return the lower value
  return low;
}

2.2 Conversion Using Stacks

As noted earlier, CPU’s execute recursive code by storing information about each recursive call in an “activation stack”.

If we wanted to convert an algorithm from a recursive form to an iterative form, we could simulate this process with our own stacks.

Any recursive algorithm can be converted to an iterative form by using a stack to capture the “history” of

• actual parameters

• local variables

that would have been placed on the activation stack.

The general idea is:

• recursive calls get replaced by push

  • depending on details, may push new values, old values, or both

• returns from recursive calls get replaced by pop

• main calculation of recursive routine gets put inside a loop

  • at start of loop, set variables from stack top and pop the stack

2.2.1 Looking at the Pieces

T recursiveFoo (U param1, V param2)
{
  U local1;
  V local2 = bar(U,V);
    ⋮  // code block 1
  recursiveFoo (local1, local2);
    ⋮  // code block 2
  recursiveFoo (param1, local2);
    ⋮  // code block 3
  recursiveFoo (local1, param2);
    ⋮  // code block 4
}

We can simulate calls to the recursive routine by saving, on a stack, all parameters and local variables. In addition, just as a “real” function call needs to know its return address, we may need to save a “location” indicator to let us know which block of code we’re supposed to execute upon a simulated return from a simulated recursive call.

It helps, then, to have a convenient structure to hold each set of information to go on the stack:

struct FooStateInfo {
  U param1;
  V param2;
  U local1;
  V local2;
  int location;
};

typedef stack<list<FooStateInfo> > FooStack;

2.2.2 Getting “parameters” from the stack

Starting with this recursive code, …

T recursiveFoo (U param1, V param2)
{
  U local1;
  V local2;
    ⋮  // code block 1
  recursiveFoo (local1, local2);
    ⋮  // code block 2
  recursiveFoo (param1, local2);
    ⋮  // code block 3
  recursiveFoo (local1, param2);
    ⋮  // code block 4
}

… we create one large control loop. Inside this loop, we have the blocks of code from the original recursive routine, but the recursive calls at the end of each block is replaced by a push of the information that we want restored upon “return” from a simulated recursive call and another push that sets up a simulated recursive call.

T iterativeFoo (U param1, V param2)
{
  U local1;
  V local2;
  FooStack stk;
  stk.push ({param1, param2, local1, local2, 1});
  while (!stk.empty())
    {
      // get parameters from stack
      const FooStackInfo& stkTop = stk.top();
      param1 = stkTop.param1;
      param2 = stkTop.param2;
      local1 = stkTop.local1;
      local2 = stkTop.local2;
      stk.pop();

      switch (stkTop.location) {
        case 1: 
             ⋮  // code block 1
           stk.push ({param1, param2, local1, local2, 2});
           stk.push ({local1, local2, local1, local2, 1});
           break;
        case 2: 
             ⋮  // code block 2
           stk.push ({param1, param2, local1, local2, 3});
           stk.push ({param1, local2, local1, local2, 1});
           break;
        case 3: 
             ⋮  // code block 3
           stk.push ({param1, param2, local1, local2, 4});
           stk.push ({local1, param2, local1, local2, 1});
           break;
        case 4: 
             ⋮  // code block 4
           break;
      }
   }
}

The final block (and any block that, in the original routine, does not do further recursive calls) does not get these pushes. If the original routine only makes recursive calls under certain conditions:

if (bar(local1, local2))
  {
   recursiveFoo(local1, local2);
  }

then the same thing happens in the iterative form with the pushes that simulate the recursive call:

if (bar(local1, local2))
  {
   stk.push ({param1, param2, local1, local2, <[..]>});
   stk.push ({local1, local2, local1, local2, 1});
  }

2.2.3 Simplifying

Now, the general approach to conversion outlined here is almost always overkill.

• We seldom need to save every parameter and local variable.

  • For example, pure inputs whose values are never changed won’t need to be put onto the stack.

• If a recursive call occurs at the very end of the routine, we might not need to set up the simulated return.

• If two or more recursive calls immediately follow one another, we can put them both on the stack immediately, rather than simulate a return in between the two.

You need to look carefully at the algorithm you are converting to see if these or other simplifications are possible.

2.3 Conversion Example: quicksort

2.3.1 Setting Up the Stack

… the only information we will need to place into our stack will be the values of low and high.

Since we only have two objects to go on the stack, we don’t need to declare a special type to hold them. The standard library provides, in <utility>, a convenient container for pairs of objects, called pair.

In this case, we would use a pair<unsigned int,unsigned int>. We can create an object of this type either by invoking the constructor:

stk.push (pair<unsigned int, unsigned int> (23, 47));

or via the function make_pair:

stk.push (make_pair(23, 47));

We can see, therefore, what kind of stack we will need, and what the push commands to simulate the recursive calls will look like.

3 Last Thoughts

Sometimes it’s really not worth converting algorithms from recursive to iterative. Some elegant, simple recursive algorithms become horrendously complicated in iterative form. On the other hand, as noted earlier, there are times when we have little choice (e.g., embedded systems).

In these kinds of situations, conversion from recursion to iteration may be the only way to get a system running.