Trees
Steven J. Zeil
Most of the data structures we have looked at so far have been devoted to keeping a collection of elements in some linear order.
Trees are the most common non-linear data structure in computer science. Trees are useful in representing things that naturally occur in hierarchies
(e.g., many company organization charts are trees) and for things that are related in a “is-composed-of” or “contains” manner (e.g., this country is composed of states, each state is composed of counties, each county contains cities, each city contains streets, etc.)
Trees also turn out to be exceedingly useful in implementing associative containers like std::set.
- Properly implemented, a tree can lead to an implementation that can be both searched and inserted into in $O(\log N)$ time.
*Compare this to the data structures we’ve seen so far, which may allow us to search in $O(\log N)$ time but insert in $O(N)$, or insert in $O(1)$ but search in $O(N)$.
1 Tree Terminology
A tree is a collection of nodes.
If nonempty, the collection includes a designated node r, the root, and zero or more (sub)trees T1, T2, … , Tk, each of whose roots are connected by an edge to r.
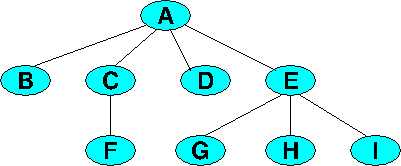
The collection of nodes shown here is a tree. We can designate A as the root, and we note that the collections of nodes {B}, {C, F}, {D}, and {E,G,H,I}, together with their edges, are all trees whose own roots are connected to A.
It’s a subtle, but important point to note that in discussing trees, we sometimes focus on the things connected to the root as individual nodes, and other times as entire trees.
The definition above focuses on a tree as a root plus a collection of (sub)trees. (The “sub” is just a convenience – there’s no formal definition of a “subtree” as opposed to a “tree”.)
1.1 All in the Family
Focusing on a tree as a collection of nodes leads to some other terminology:
-
Each node except the root has a parent.
-
Parent nodes have children. Nodes without children are leaves.
-
Nodes with the same parent are siblings.
1.2 Binary Trees
-
A tree in which every parent has at most 2 children is a binary tree.
-
Trees in which parents may have more than 2 children are general trees.

This, then is a general tree.
1.3 Paths
- A path from $n_1$to $n_k$ is a sequence $n_1 ,n_2, … ,n_k$ such that
\[ \forall i, 1 \leq i < k, n_i \; \mbox{is the parent of} \; n_{\mbox{i+1}}. \]
-
The length of a path is the number of edges in it.
-
$n_1$ is an ancestor of $n_k$.
-
$n_k$ is a descendant of $n_1$.
-

Question: Which of the following sequences of nodes are paths? (May be more than one)
-
[C, A, E, G]
-
[A, E, G]
-
[E]
-
[]
1.4 Depth & Height
-
The depth of a node is the length of the path from the root to that node.
-
The height of a node is the length of the longest path from it to any leaf.
-
The height of an empty tree is -1.

Question: What is the height of E?
2 Tree Traversal
Many algorithms for manipulating trees need to “traverse” the tree, to visit each node in the tree and process the data in that node. In this section, we’ll look at some prototype algorithms for traversing trees, mainly using recursion.
Later, we’ll look at how to devise iterators for tree traversal. But iterators are primarily for application code. The underlying implementation of a tree-based ADT will still need to employ the kinds of algorithms we are about to discuss.
2.1 Kinds of Traversals
-
A pre-order traversal is one in which the data of each node is processed
beforevisiting any of its children. -
A post-order traversal is one in which the data of each node is processed
aftervisiting all of its children. -
An in-order traversal is one in which the data of each node is processed after visiting its left child but before visiting its right child.
-
This traversal is specific to binary trees.
-
-
A level-order traversal is one in which all nodes of the same height are visited before any lower nodes.
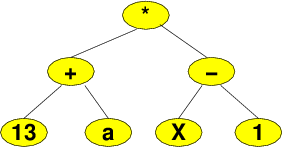
Compilers, interpreters, spreadsheets, and other programs that read and evaluate arithmetic expressions often represent those expressions as trees. Constants and variables go in the leaves, and each non-leaf node represents the application of some operator to the subtrees representing its operands. The tree here, for example, shows the product of a sum and of a subtraction.
If we were to traverse this tree, printing each node as we visit it, we would get:
- Pre-order
- * + 13 a - x 1
- In-order
-
13 + a * x - 1
Compare this to ((13+a)*(x-1)), the “natural” way to write this expression. You can see that in-order traversal yields the normal way to write this expression except for parentheses. If we made our output routine put parentheses around everything, we would actually get an algebraically correct expression.
When applied to a “binary search tree”, which we will introduce in a later lesson, in-order traversal processes the nodes in sorted order.
- Post-order
-
13 a + x 1 - *
Post-order traversal yields post-fix notation, which in turn is related to stack-based algorithms for expression evaluation.
- Level-order
- * + - 13 a x 1
2.2 Recursive Traversals (Binary Trees)
Let’s suppose that we have a binary tree whose nodes are declared as shown here.
This is a typical binary tree structure, with a field for data and pointers for up to two children. If the node is a leaf, both the left and right pointers will be null. If the node has only one child, either the left or right will be null.
It’s fairly easy to write pre-, in-, and post-order traversal algorithms using recursion.
template <typename T>
void basicTraverse (BiTreeNode<T>* t)
{
if (t != 0)
{
basicTraverse(t->left);
basicTraverse(t->right);
}
}
This is the basic structure for a recursive traversal. If this function is called with a null pointer, we do nothing. But if we have a real pointer to some node, we invoke the function recursively on the left and right subtrees. In this manner, we will eventually visit every node in the tree.
- The problem with the basic traversal algorithm is that it don’t do anything with the data in the trees.
2.2.1 Pre-Order Traversals
But we can convert the basic traversal into a pre-order traversal by applying the rule:
process the node before visiting its children
template <typename T>
void preorder(BiTreeNode<T> *t)
{
// the recursive scan terminates on a empty subtree
if (t != nullptr)
{
doSomethingWith (t->nodeValue);
preorder(t->left); // descend left
preorder(t->right); // descend right
}
}
2.2.2 Post-Order Traversals
We get a post-order traversal by applying the rule:
process the node after visiting its children
template <typename T>
void postorder(BiTreeNode<T> *t)
{
// the recursive scan terminates on a empty subtree
if (t != nullptr)
{
postorder(t->left); // descend left
postorder(t->right); // descend right
doSomethingWith (t->nodeValue);
}
}
2.2.3 In-Order Traversals
And we get an in-order traversal by applying the rule:
process the node after visiting its left descendants and before visiting its right descendants.
template <typename T>
void inorder(BiTreeNode<T> *t)
{
// the recursive scan terminates on a empty subtree
if (t != nullptr)
{
inorder(t->left); // descend left
doSomethingWith (t->nodeValue);
inorder(t->right); // descend right
}
}
Note that, while pre- and post- order traversals can be applied to trees with any number of children, in-order really only makes sense when applied to binary trees.
Try out the traversals in an animation. Try these with different trees until you are comfortable with them.
2.3 Recursive Traversals (General Trees)
When we work with general trees, we have to allow for an arbitrary number of children. So, instead of data members like left and right to hold individual children, we use a sequence container of some type to hold pointers to all of the children.
Let’s suppose that we have a general tree whose nodes are declared as shown here.
We have used a vector to hold the pointers to the children. Unlike binary trees, we won’t use null pointers to indicate that a child is missing. Anything that is “missing” will simply never have been added to the vector. If the node is a leaf, the children vector will have size zero.
A basic traversal of a general tree looks like this
template <typename T>
void basicTraverse (TreeNode<T>* t)
{
if (t != 0)
{
for (TreeNode<T>* child: t->children)
basicTraverse(child);
}
}
This is the basic structure for a recursive traversal. If this function is called with a null pointer, we do nothing. But if we have a real pointer to some node, we invoke the function recursively on the children. In this manner, we will eventually visit every node in the tree.
It’s fairly easy to rewrite the pre- and post-order traversal algorithms to accommodate the arbitrary number of children.
Again, to make this useful, we need to add code to actually do something with the data in each node.
The most common places to do this are just before or just after visiting all the children.
2.3.1 Pre-Order Traversals
process the node before visiting its children
template <typename T>
void preorder(TreeNode<T> *t)
{
if (t != 0)
{
doSomethingWith (t->nodeValue);
for (TreeNode<T>* child: t->children)
basicTraverse(child);
}
}
2.3.2 Post-Order Traversals
process the node after visiting its children
template <typename T>
void postorder(TreeNode<T> *t)
{
template <typename T>
void preorder(TreeNode<T> *t)
{
if (t != 0)
{
for (TreeNode<T>* child: t->children)
basicTraverse(child);
doSomethingWith (t->nodeValue);
}
}
}
Note that, while pre- and post- order traversals can be applied to trees with any number of children, in-order really only makes sense when applied to binary trees.
2.4 Level-Order Traversal
This form of traversal is different from the others. In a level-order traversal, we visit the root, then all elements 1 level below the root, then all elements two levels below the root, and so on. Unlike the other traversals, elements visited successively may not be related in the parent-child sense except for having the root as a common (and possibly distant) ancestor.
To program a level-order traversal, we use a queue to keep track of nodes at the next lower level that need to be visited.
Here’s an algorithm for level-order traversal of a general tree. You can adapt this for us with binary trees as well, though in my experience level-order traversals seem more likely to arise in general-tree problems.
template <typename T>
void levelOrder (TreeNode<T>* t)
{
// store siblings of each node in a queue so that they are
// visited in order at the next level of the tree
queue<TreeNode<T> *> q;
TreeNode<T> *p;
// initialize the queue by inserting the root in the queue
q.push(t);
// continue the iterative process until the queue is empty
while(!q.empty())
{
// delete front node from queue and output the node value
p = q.front();
q.pop();
doSomethingWith (t->nodeValue);
// Add the children onto the queue for future processing
for (TreeNode<T>* child: children)
q.push(child);
}
}
The code discussed here is available as an animation that you can run to see how it works.
3 Example: Computing the Tree Height
As an example of applying a tree traversal, let’s consider the problem of computing the height of a tree.
Remember that the height of a tree node was defined as “the length of the longest path from it to any leaf”.
That means that, if we knew the height of each of that node’s children, the height of this node would be one more than that of it’s “tallest” child.
int height = 1 + max(leftChildHeight, rightChildHeight);
This suggests that we much compute the height of a node’s children before we can compute the height of the node itself. That means that we can look to a post-order traversal: compute something for each child before computing it for the parent.
Our basic post-order traversal code looks like:
template <typename T>
void postorder(BiTreeNode<T> *t)
{
// the recursive scan terminates on a empty subtree
if (t != nullptr)
{
postorder(t->left); // descend left
postorder(t->right); // descend right
doSomethingWith (t->nodeValue);
}
}
To use this to compute the height, we would do
template <typename T>
int height(BiTreeNode<T> *t)
{
// the recursive scan terminates on a empty subtree
if (t != nullptr)
{
int leftChildHeight = height(t->left); // descend left
int rightChildHeight = height(t->right); // descend right
int height = 1 + max(leftChildHeight, rightChildHeight);
return height;
} else {
return -1; // height of an empty tree is -1
}
}
You should still be able to recognize the pattern of a post-order traversal in this code.
We could even streamline this as
template <typename T>
int height(BiTreeNode<T> *t)
{
// the recursive scan terminates on a empty subtree
if (t != nullptr)
{
return 1 + max(height(t->left), height(t->right));
} else {
return -1; // height of an empty tree is -1
}
}
and it would still be a post-order traversal (because the height calculation does not take place until we have returned form both recursive calls), even if it is a little harder to recognize as such.
A general tree version of this works along similar lines:
template <typename T>
int height(TreeNode<T> *t)
{
// the recursive scan terminates on a empty subtree
if (t != nullptr)
{
int maxHeight = -1;
for (TreeNode<T>* child: t->children)
{
maxHeight = max(maxHeight, height(child));
}
return 1 + maxHeight;
} else {
return -1; // height of an empty tree is -1
}
}
4 Example: Processing XML
XML is a markup language used for exchanging data among a wide variety of programs on the web. It is flexible enough to represent almost any kind of data.
In XML, data is described by structures consisting of nested “elements” and text. An element is described as an opening “tag”, the contents of the element, and a closing tag.
Tags are written inside < > brackets. Inside the brackets, an opening tag has a tag name followed by zero or more “attributes”. An attribute is a name="value" pair, with the value inside quotes. Closing tags have no attributes, and are indicated by placing the tag name immediately after a ‘/’ character.
Finally, if an element has no text and no internal elements, it can be written as
<tag attributes></tag>
or abbreviated as
<tag attributes />
As an example of XML, here is a question from a quiz, in the XML form that serves as input to an on-line quiz generator:
<Question type="Choice" id="ultimate">
<QCategory>trial</QCategory>
<Body>What is the answer to the ultimate question of life,
the universe, and everything?
</Body>
<Choices>
<Choice>a good nap</Choice>
<Choice value="1">42</Choice>
<Choice>inner peace</Choice>
<Choice>money</Choice>
</Choices>
<AnswerKey>42</AnswerKey>
<Explanation>
D Adams, The Hitchhiker's Guide to the Galaxy
</Explanation>
<Revisions>5/15/2001 1:35:29 PM</Revisions>
</Question>
Although it may not be obvious, XML actually describes a tree structure.
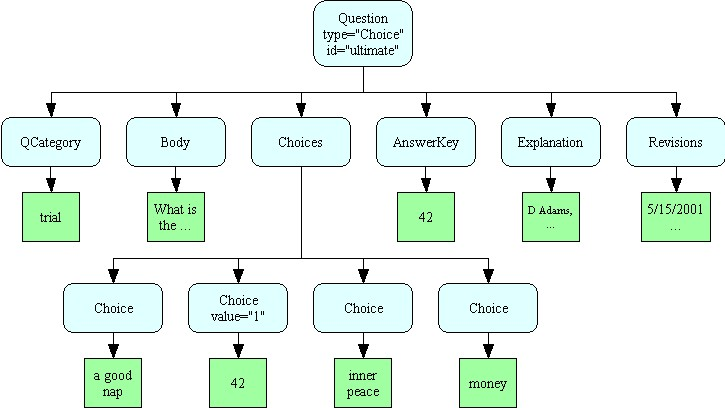
For example, the structure above shows that all the elements are inside a “Question”. One of those elements inside the Question is a “Choices” element, and each individual “Choice” occurs inside there. We can diagram this tree structure as shown here.
If this description of XML sounds familiar, you may be noticing it’s close relationship to HTML, the web page markup language. HTML is almost a kind of XML in which all the elements are chosen as descriptions of different text formatting properties and different portions of a web page. Actually, HTML does not follow all the rules of XML (attributes can often be written without placing the value in quotes, empty elements can be written as <tagname> instead of <tagname/>, and some non-empty elements can be written without a closing </tagname>). HTML and XML are closely related enough that there are a number of programs, such as the Unix tidy command, that will rewrite an HTML page into “proper” XML.
For example, the text shown here can be produced by the following XML-legal HTML (a.k.a., xhtml):
<html>
<head>
<title>Just a Test</title>
</head>
<body>
<h1>Just a test</h1>
<p>Nothing much to
see <a href="test.html">here</a>.
</p>
<p>
Move <a href="nextpage.html">along</a>.
</p>
</body>
</html>
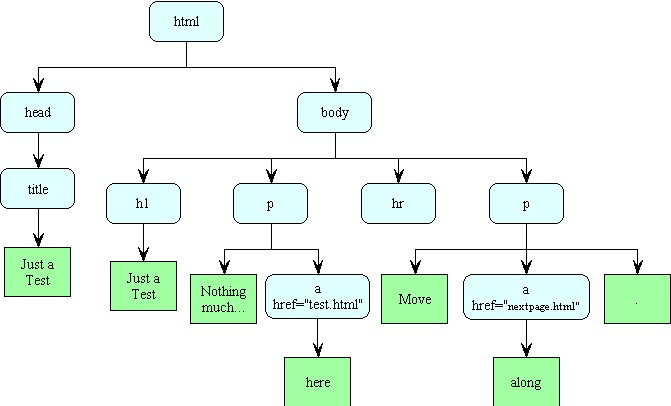 The tree structure for that HTML page is shown here.
The tree structure for that HTML page is shown here.
Now suppose that we wished to write a program that would read a web page and print a list of all links (<a>elements with href= attributes). Although we could certainly write such a program entirely from scratch, XML is popular enough that should expect there to be at least a few libraries that will include code to read web pages and to prepare the tree structure (called the DOM for “Domain Object Model”) for us.
/** Example of tree manipulation using XML documents */
#include <iostream>
using namespace std;
#include <xercesc/parsers/XercesDOMParser.hpp>
#include <xercesc/dom/DOM.hpp>
#include <xercesc/sax/HandlerBase.hpp>
#include <xercesc/util/XMLString.hpp>
#include <xercesc/util/PlatformUtils.hpp>
using namespace XERCES_CPP_NAMESPACE;
DOMDocument* readXML (const char *xmlFile)
{
⋮
}
string getHrefAttribute (DOMNode* linkNode)
{
DOMElement* linkNodeE = (DOMElement*)linkNode;
const XMLCh* href = XMLString::transcode("href");
const XMLCh* attributeValue = linkNodeE->getAttribute(href);
return string(XMLString::transcode(attributeValue));
}
void processTree (DOMNode *tree)
{
if (tree != nullptr)
{
if (tree->getNodeType() == DOMNode::ELEMENT_NODE)
{
const XMLCh* elName = tree->getNodeName();
const XMLCh* aName = XMLString::transcode("a");
if (XMLString::equals(elName, aName))
cout << "Link to " << getHrefAttribute(tree) << endl;
}
for (DOMNode* child = tree->getFirstChild();
child != nullptr; child = child->getNextSibling())
processTree(child);
}
}
int main(int argc, char **argv)
{
if (argc != 2)
{
cerr << "usage: " << argv[0] << " xmlfile" << endl;
return 1;
}
// Initialize the Xerces XML C++ library
try {
XMLPlatformUtils::Initialize();
}
catch (const XMLException& toCatch) {
char* message = XMLString::transcode(toCatch.getMessage());
cout << "Error during initialization! :\n"
<< message << "\n";
XMLString::release(&message);
return 1;
}
DOMDocument* doc = readXML(argv[1]);
if (doc == 0)
{
cerr << "Could not read " << argv[1] << endl;
return 2;
}
processTree (doc->getDocumentElement());
// Cleanup
doc->release();
return 0;
}
Here is my code for listing the links in an HTML file, based upon the Xerces-C++ library.
void processTree (DOMNode *tree)
{
if (tree != nullptr)
{
if (tree->getNodeType() == DOMNode::ELEMENT_NODE)
{
const XMLCh* elName = tree->getNodeName();
const XMLCh* aName = XMLString::transcode("a");
if (XMLString::equals(elName, aName))
cout << "Link to " << getHrefAttribute(tree) << endl;
}
for (DOMNode* child = tree->getFirstChild();
child != nullptr; child = child->getNextSibling())
processTree(child);
}
}
If this code is compiled and run on the HTML page we have just seen, it would print
Link to test.html
Link to nextpage.html
Question: Now, this code features an interface that you have never seen before, and a lot of the details are bound to look mysterious. Nonetheless, if you look at the processTree function, you can readily tell that this function works by
-
pre-order traversal
-
in-order traversal
-
post-order traversal
-
level-order traversal


