Context-Free Grammars -- Examples
CS390, Spring 2024
Abstract
Practice designing and working with CFGs, derivations, and parse trees.
1 Automat
-
Read about Grammars in the Automat Editor.
-
Use the editor to solve Exercises 5.1.2 b and c from your textbook.
-
Enter the grammar
\[ \begin{align} E &\rightarrow I \\ E &\rightarrow E + E \\ E &\rightarrow E * E \\ I &\rightarrow a \\ I &\rightarrow b \\ I &\rightarrow Ia \\ I &\rightarrow Ib \\ I &\rightarrow I0 \\ I &\rightarrow I1 \\ \end{align} \]
-
Test the string “a $*$ b + a1”.
-
Generate a derivation of that string. Save the URL of your grammar and derivation.
-
Copy that URL to a new tab/window. Clear the derivation.
In this second window, show that this grammar is ambiguous by deriving two distinct parse trees for “a $*$ b + a1”.
2 Sample Problems
The problems in this section are all concerned with the following grammar:
\[ \begin{align} P \rightarrow & S \\ L \rightarrow & S L | S\\ S \rightarrow & s ; | \{ L \} \\ \end{align}
\]
A discussion of what this grammar “means” and how to read it:
2.1 Derivations
-
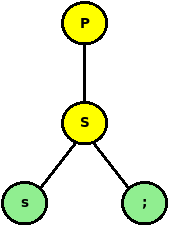
Give a derivation for the string:
s;Reveal -
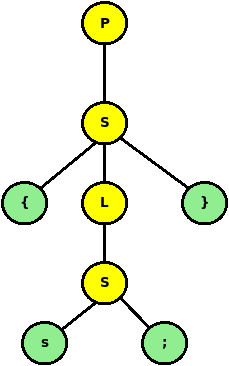
Give a derivation for the string
{s;}Reveal -
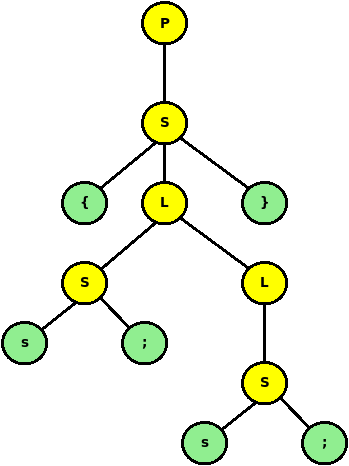
Give a (left-most) derivation for the string
{s;s;}RevealUsing recursion in context-free grammars to describe lists of things is a very common pattern, one that you should try to keep in mind both when reading grammars and when writing your own.
-
Give a right-most derivation for the string
{s;s;}Reveal
2.2 Parse Trees
-
Give a parse tree for the string:
s;Reveal -
Give a parse tree for the string
{s;}Reveal -
Give a parse tree for the string
{s;s;}Reveal
The grammar we have used in these examples was intended to be reminiscent of the idea of a program (P) consisting of either a single statement (S) or a list of statements (L) enclosed in brackets. We can actually expand on this idea to make rhe relationship clearer by replacing the simple idea that a “statement” is simply a single token (s) by the idea that s could go on to derive any of a number of more familiar forms of programming language constructs.
3 Sample Problems – Ambiguity
We’ll continue working with the grammar:
\[ \begin{align} P \rightarrow & S \\ L \rightarrow & S L \; | \; S\\ S \rightarrow & s ; \\ & | \, \{ L \} \\ & | \, i \, ( \, E \, ) \, S \\ & | \, i \, ( \, E \, ) \, S \, e \, S \\ E \rightarrow & x | y \end{align}
\]
This grammar can generate the possible sequences of if and else (represented by i and e, respectively).
-
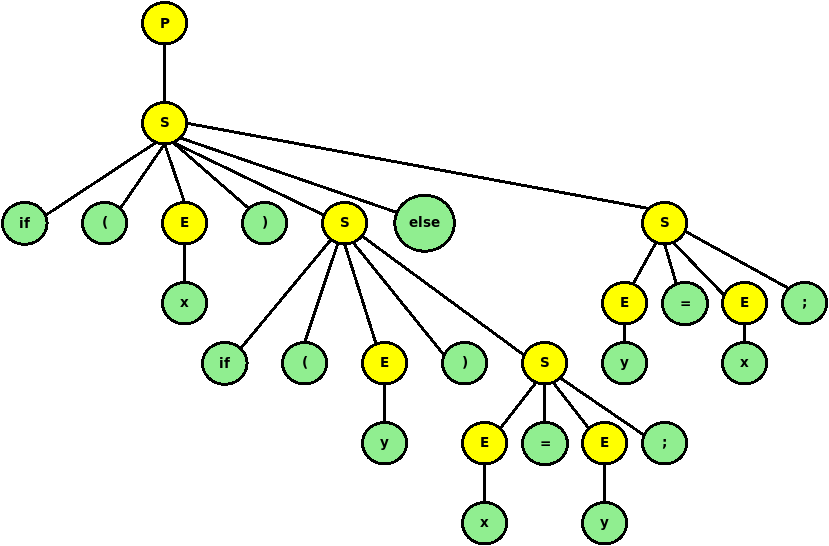
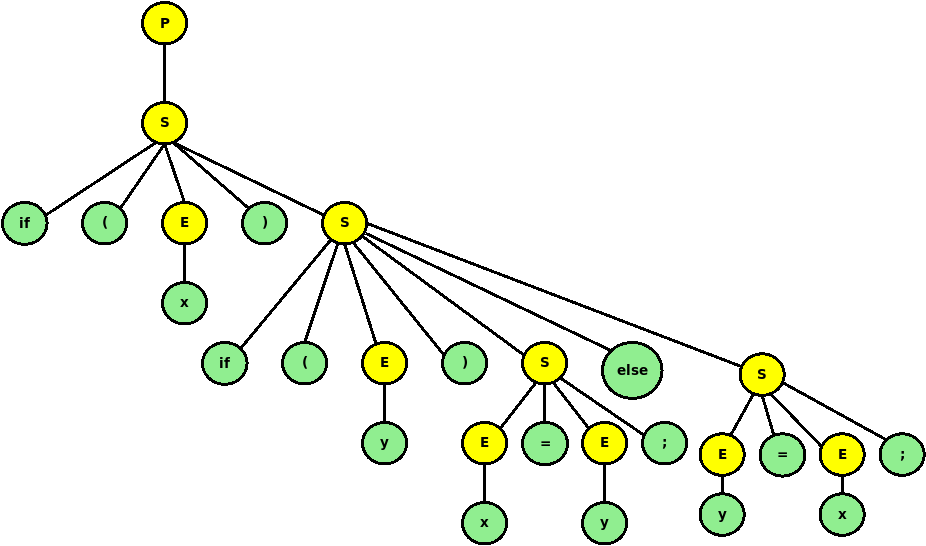
Show that the string ‘$i (x) \, i (y) \, x = y; e \, y = x;$’ is in the language described by this grammar.
Reveal -
Give a left-most derivation for that string.
Reveal -
Using that same string, show that the grammar is ambiguous
Reveal
Some discussion of why ambiguity is both important and can be hard to prove/disprove.