Nondeterministic Finite State Automata: Examples
CS390, Spring 2024
Abstract
Practice designing and working with NFAs.
1 Working with Automat
-
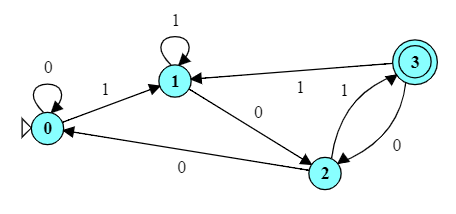
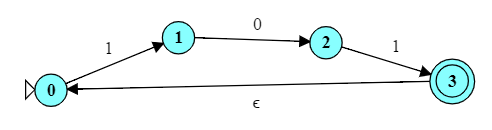
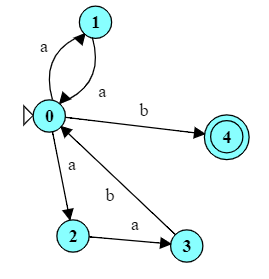
The NFA shown to the right is intended to accept the language $\{aa,aab\}^{*}\{b\}$.
Although it has no $\epsilon$ transitions, it is, nonetheless, nondeterministic because state $q_0$ has two different transitions on the same input symbol,
a.Try running it on each of the following inputs to see if it works as expected:
- b
- aa
- aab
- aabb
- aaab
- aaaab
- aaaabb
- aaaabbb
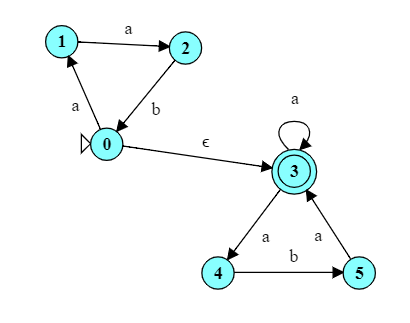
-
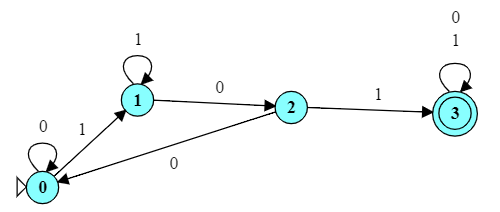
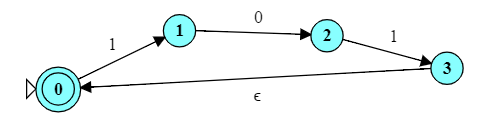
The NFA on the right uses an $\epsilon$ transition to help recognize the language $\{aab\}^*\{a,aba\}^*$. Look at the figure and compare to the structure of the set expression. Can you see how each element of the set expression is reflected in the arrangement of the states and transitions?
Try running it on each of the following inputs to see if it works as expected:
- a
- aa
- aab
- aba
- aaba
- aabaab
- aabaaba
- aababa
- abaaab
-
Revisit some of the DFA problems that you worked in the final step of the earlier DFA exercise. Try rewriting some of them as NFAs.
-
In many cases, an NFA will use fewer states and transitions than the corresponding DFA. Certainly, it should never need more states or transitions than a DFA (because every DFA is also an NFA that just happens to not use non-determinism).
-
You can think of this simplification as the pay-off for the slightly more complicated conceptual effort involved in understanding non-determinism.
-
-
Exercise 2.3.4 at the end of section 2.3 2 of your text suggests drawing a number of NFAs. Pick one or two of these and create them. Run a handful of inputs through each one to convince yourself that you have done so correctly.
2 Sample Problems
Try to solve these on your own, first, then check my answer. If you don’t see where I got my answer from, the videos will walk you through my thought process.
2.1 Basic Patterns
Design an NFA to recognize the language consisting of…
-
the string 101
Reveal -
all strings beginning with 101
Reveal -
all strings ending with 101
Reveal -
all strings containing 101
Reveal
2.2 Combining Smaller Machines into Larger Ones
2.2.1 Sequencing
Putting two NSAs together in a sequence is, roughly speaking, accomplished by “connecting” each final state of the first FSA to the starting state of the second one with an $\epsilon$ transition.
No merging is required.
Design an FSA to recognize the language consisting of…
- all strings beginning with and ending with 101
Reveal
2.2.2 Alternation (Choice)
Join the alternatives at initial and accepting states to a common start and end with $\epsilon$ transitions.
Design an FSA to recognize the language consisting of…
- strings beginning with 101 or 110
Reveal
2.2.3 Repetition
Design an FSA to recognize the language consisting of…
-
All strings containing one or more instances of 101
Reveal -
All strings containing zero or more instances of 101
Reveal -
all strings composed of 1 or more (non-overlapping) occurrences of 101
Reveal -
all strings composed of zero or more occurrences of 101 only
Reveal -
all strings that do not contain 101
Reveal
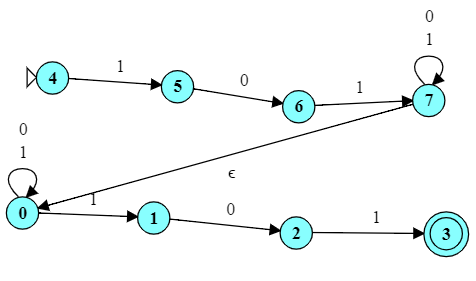
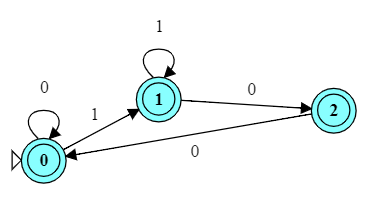
2.3 Converting An NFA to a DFA
- Convert the automaton below to a deterministic FA.
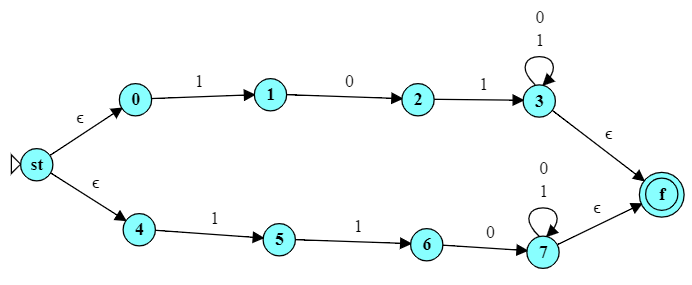 Reveal
Reveal
^


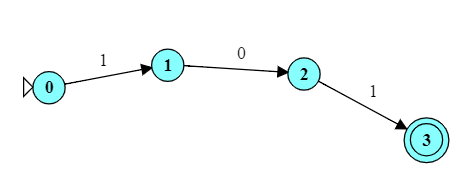
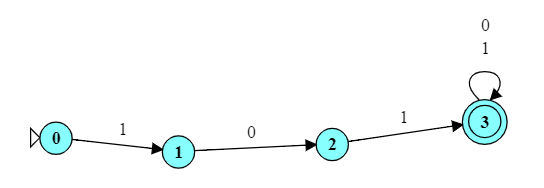
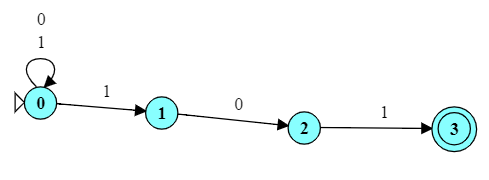
 (video)
(video)