Nondeterministic Finite Automata
CS390, Spring 2024
Abstract
Next consider an extension of our FA model that allows nondeterminism, a kind of parallel processing. We call the result a nondeterministic finite automata (NFA). Curiously, we will show that although NFAs make it easier to describe some languages, the parallelism does not actually increase the power of our automata.
These lecture notes are intended to be read in concert with Chapter 2.3-2.6 of the text (Ullman).
1 Nondeterminism
Nondeterminism usually refers to process or computation that can have more than one result even when its input is fixed. In the real world, we often view things as non-deterministic because there are inputs that we cannot control (e.g., “If I throw this frisbee at a target, I expect it to hit, but if there’s a sudden gust of wind, I might miss.”) or cannot perceive (e.g., “I swear that I’ve used the exact same motion and strength to flip this coin each time, yet I can’t control whether it comes up heads or tails”).
One of the revolutions in Physics was quantum mechanics, which argued that the universe was not, as 19th century physicists had believed, a complex but predictable “clockwork” mechanism, but was instead fundamentally based on probabilities (Sometimes the electron jumps states, sometimes it doesn’t. Sometimes the cat lives. Sometimes it dies.)
We can predict what is most probable, but cannot say with absolute certainty that almost anything definitely will or will not happen.1
Ullman et al. consider two different ways of introducing non-determinism.
-
One is to simply relax the rule that says that, for any given input, there can only be a single transition to another state. By allowing the same input to take you to two or more states, the overall behavior of the automaton becomes harder to predict because it can be in multiple states at once, with each of those states contributing new transitions on subsequent inputs.
-
A second way to introduce non-determinism is to allow instantaneous transitions from one state to others without waiting for the next input characters. These are modeled as transitions on a special character $\epsilon$, and these transitions are therefore referred to as $\epsilon$-transitions.
Now, $\epsilon$ is the symbol used earlier to denote an empty string, i.e., $\epsilon$ == "". But FAs don’t do transitions on entire strings, they do transitions on individual characters. So we’re playing a little game here. We introduce a special character that’s not in our regular alphabet. We’ll call it $\epsilon$ because, well, because we can. We’re going to introduce a special rule that, when translating strings from our augmented alphabet to the original alphabet, that it behaves like the empty string $\epsilon$. For any strings $u$ and $v$,
\[ u\epsilon v \rightarrow uv \]
So this “translation” rule works as expected whether the “$\epsilon$” is the empty string or the special character.
Then we pretend that all of our inputs (in the original alphabet) are augmented by placing a whole bunch (i.e., as many as we have states in the automaton) of these special characters before and after each of the original characters. e,g, the input $abc$ becomes $\epsilon\epsilon\ldots\epsilon a\epsilon\epsilon\ldots b\epsilon\epsilon\ldots c\epsilon\epsilon\ldots$.
If we are willing to play all of these games, an NFA with $\epsilon$-transitions is actually just an “ordinary” NFA in which we can have transitions to multiple states on the same input.
1.1 Example: Taking the union of two languages
To see how this would be useful, consider the problem of finding an automaton that describes the union of two languages for which we already have FAs.
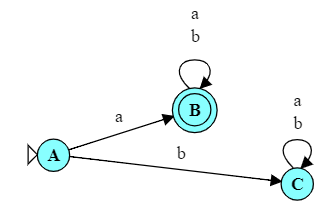
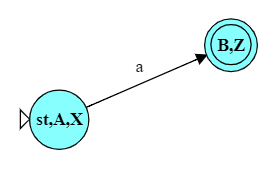
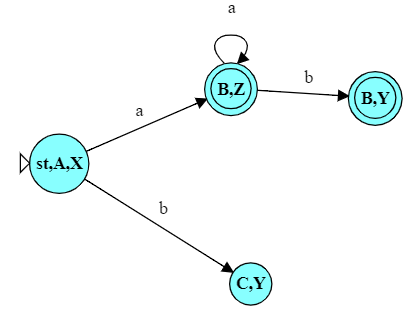
For example, consider the language of all strings over the alphabet $\{a, b\}$ that begin with ‘a’. A DFA for this language is shown here.
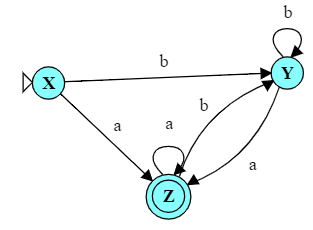
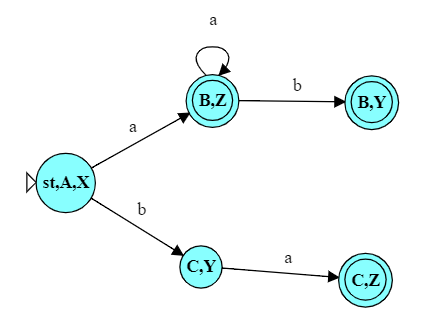
Then consider the language of strings (over the same alphabet) in which every ‘b’ is (eventually) followed by an ‘a’. An automaton for that language is shown here.
Now, suppose that I want to construct an automaton for the union of these languages: the set of strings that begin with ‘a’ or that have every ‘b’ followed by an ‘a’.
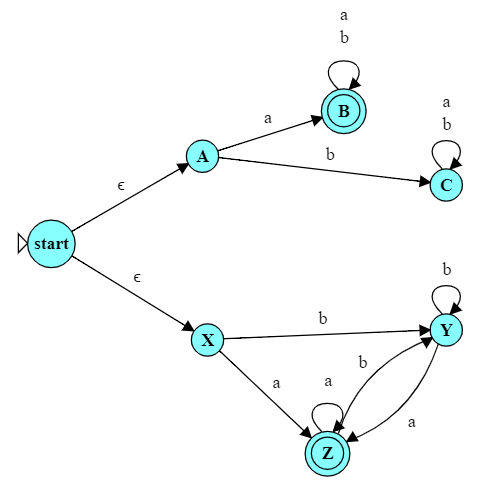
We can do that very easily by simply allowing those two automata to run “in parallel” on the same input. We add a new start state for the combined automaton, but add a pair of $\epsilon$-transitions to immediately transition into the original start states of the two DFAs.
Notation warning: Many authors in this area use $\epsilon$ to represent empty strings and, therefore, simultaneous transitions in NFAs.
Many others use $\lambda$ for the exact same purposes, however.
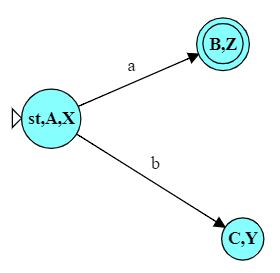
So, before we see a single “real” character, we transition into two new states, in effect “activating” both of the original automata. They will then start accepting input characters simultaneously. After any given input string, if either of the original DFAs would have been in a final state, our combined automaton will be in a final state as well.
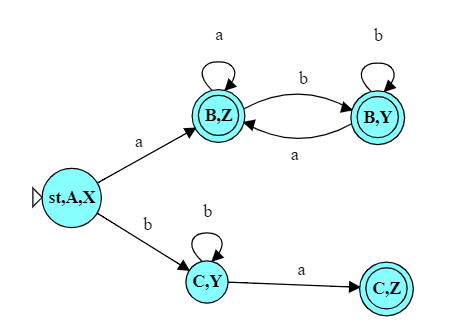
For example, after the input “abbb”, we will be in states B and Y, and state B is a final state. After the input “baa”, we will be in states C and Z, and Z is a final state. On the other hand, after the input “bb”, we would be instates C and Y, neither of which is final.
Try running this NFA on the strings
abbbandabababand verify that it works as I have claimed.
1.2 Example: Decomposition of Set Expressions
In an earlier example on creating DFAs, we looked at how to systematically construct a DFA from simple set expressions. I stated then that
“This whole approach will be easier for the NFAs we discuss later than for DFAs, because they allow sub-solutions to be linked together more easily.”
Let’s take at a look at that process.
If I asked you, for example, to create an FA for, say, $\{01,101\}^*$, that breaks down into
-
the *, a “loop” that has to come back to its starting state
-
the body of the loop, consisting of
-
a choice between
- a concatenation of two characters 0, 1, and
- a concatenation of three characters 1, 0, 1
-
So you could…
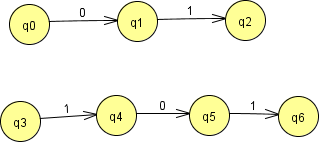
… start by writing out the straight-line sequences for the two concatenations.
Then, because the expression $\{01,101\}$ involves choosing either of these set elements, we tie them together at their beginning and their end to indicate a “union” or “either-or” structure.
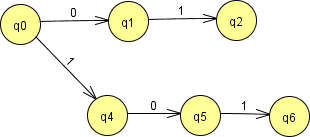
For DFAs, you may recall, tying these together required merging the beginning states, as shown here. Later we merged the end states as well.
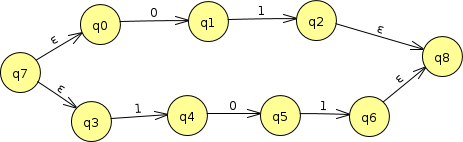
But when constructing an NFA, we can instead leave the original sequences untouched and join them using $\epsilon$-transitions, as shown here. This expresses the idea that “you can go to this subexpression or that subexpression” in an easily recognized form.
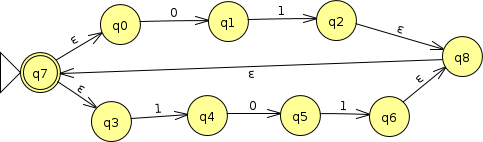
Then we add the * in $\{01,101\}^*$ by simply connecting the end back to the beginning so that we can do any number of repetitions.
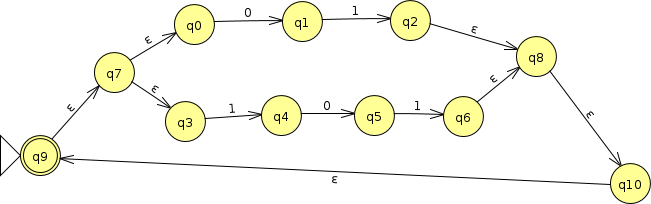
Or we can, as we did for the union a moment ago, add a new begin and end state, joined to the inner subexpression with $\epsilon$-transitions.
Each of these last two automata will not only recognize the language $\{01,101\}^*$, but will do so in a way that can be easily recognized by someone reading the patterns in the NFA itself.
We’ll formalize this approach in the next module.
2 Every NFA can be reduced to a DFA
DFAs and NFAs are fundamentally equivalent. Every language that can be accepted by an DFA can be also be accepted by some NFA, and vice-versa.
It’s not hard to show that every language accepted by a DFA can be accepted by some NFA. That’s because an NFA is actually a relaxed form of the definition of a DFA. Every DFA is itself also an NFA – it’s just one in which we have not taken advantage of any of the extra possibilities permitted to the nondeterministic form.
Proving that the language accepted by any NFA can also be accepted by some DFA is harder, but much more interesting. That’s because the proof amounts to an algorithm for converting an NFA into an equivalent DFA.
I’m not going to type out all of the formal arguments from the text, but I do want to highlight some of the key ideas that lead to the conversion algorithm.
First, of the five components that make up an NFA $A = (Q, \Sigma, \delta, q_0, F)$,
- The alphabet $\Sigma$ stays the same.
- The set of states $Q$ and the function $\delta$ that controls the transitions between them will, obviously, change. Our algorithm will be tasked with computing these.
- Similarly, the conversion algorithm will need to figure out what, in the new DFA, corresponds to the original starting state $q_0$ and which of the newly created states are to be final.
2.1 Subsets as State Labels
The defining characteristic of an NFA is that it can be in multiple states at once. So the “labels” for our new DFA states will actually be a set of the original state labels from the NFA. For example, if we can find an input for which an NFA can simultaneously be in states A and Y, the generated DFA will have a state labeled ${A,Y}$. (This is a set of the original labels because order doesn’t matter. having decided to label one DFA state ‘AY’, if we should ever be tempted to create a state ${Y,A}$, we will have to remember that these are actually the same state because ordering does not matter in sets.
Now, in the absolute worst case, we might anticipate that, given the right inputs, we could drive an NFA into any possible combination of its states. That would mean that an NFA with $N$ states could translate into a DFA with as many as $2^N$ states – one for each possible subset of the set of states in the NFA. That doesn’t happen often – most practical problems would see a much smaller growth in the number of states – but it actually illustrates a big reason why we use NFAs in the first place. They can allow us to describe a language in much more compact form than if we were using a DFA.

Once we understand that the labels of our new DFA states will be sets of labels from the original NFAs, it is easy to see how the final states will be identified. Any DFA state whose label includes a final NFA state will, itself, be final.
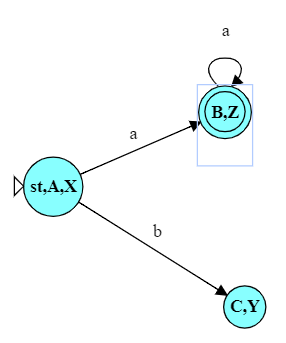
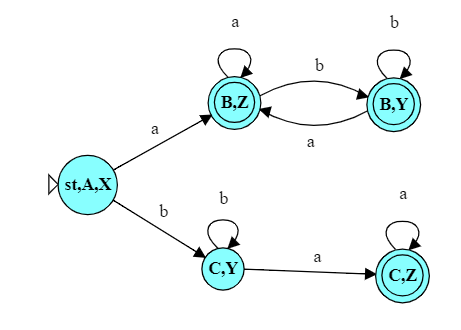
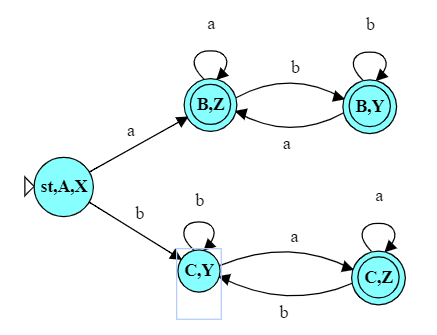
So if, for example, we were converting this NFA to a DFA and discovered, at the end, a state $\{C,Y\}$, that would not be final because neither C nor Y are final in the original NFA. But if our converted DFA has states $\{C,Z\}$ or $\{B,Y\}$, those would be final because Z is final and B is final, respectively.
2.2 $\epsilon$-Closure
A key idea in the conversion algorithm is the $\epsilon$-closure of a set of states. The $\epsilon$-closure of a single state s would be the set consisting of s and all states that can be reached from s by following only $\epsilon$-transitions.
The $\epsilon$-closure of an entire set of states S would be the union of the $\epsilon$-closures of all the elements of S.

For example,
\[ \epsilon\mbox{-closure}(\mbox{start}) = \{\mbox{start}, A, X\} \]
But
\[ \epsilon\mbox{-closure}(A) = \{A\} \]
In fact, for this automaton, the $\epsilon$-closure of every state except start is simply that state itself.
2.3 The Conversion Algorithm
The conversion algorithm, referred to as a “subset construction”, then has the structure
-
The starting state of the new DFA will be labeled with the $\epsilon$-closure of $q_0$, the starting state of the NFA. Add that to a queue of not-yet-analyzed states.
-
Pick a state labeled $s_1 s_2 \ldots$ from that queue. For each symbol
ain the alphabet, consult the NFA to see what states it enters when starting from one of those states in the label. Take the union of all those, and then take the $\epsilon$-closure of that union. The result $t_1 t_2 \ldots$ is the label of a state in the new DFA.If $t_1 t_2 \ldots$ is not already a state in our DFA, add it to the DFA and to the queue of not-yet-analyzed states.
Whether it was a new state or not, add a transition in our DFA from $s_1 s_2 \ldots$ to this $t_1 t_2 \ldots$.
-
Repeat step 2 until the entire queue has been processed.
CS361 students should recognize this use of a queue as a variation of breadth-first traversal of a data structure.
2.4 Example

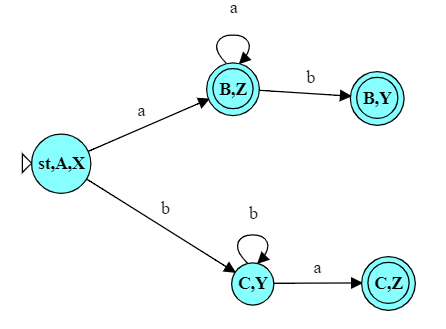
If we were to convert this NFA, for example, …
Try running this converted automaton and the original NFA on inputs
bbb,abbb, andababaand confirm for yourself that this new DFA is equivalent to the NFA.
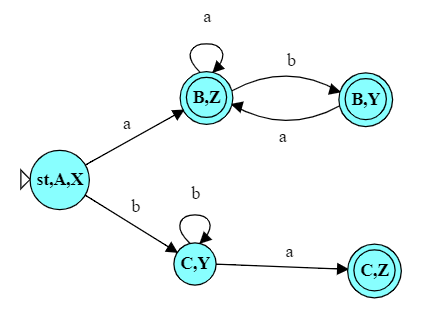
This algorithm converts NFAs to DFAs, but it does not always find the smallest possible DFA (i.e., fewest states) for that language.
As an example, look at the DFA we have just constructed. It’s pretty clear that, one we have entered state B,Z, we are going to accept no matter what remains in the string. We really don’t need the state B,Y.
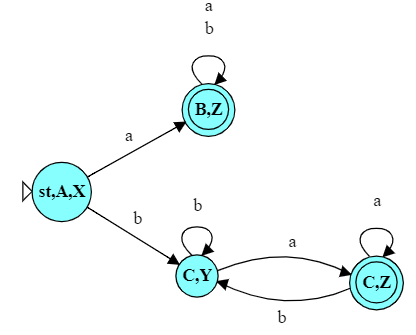
So we could simplify that DFA, reducing both the number of states and the number of transitions.
3 Closing Thoughts: Nondeterminism and Programming
When we begin learning to program, we place a high value on determinism. We rely on the fact that, for example, that if we repeatedly feed in the same input to a program, that program will always give us the same output. Think how important that is to you generally when trying to test and debug your code!
But, in the back of our minds, we understand that there are external influences that can change this deterministic behavior. If other processes on the same computer steal all of the available memory, for example, our usually reliable computer may crash in strange and unpredictable ways. As we begin to consider things like GUIs, the timing of inputs is often as important as the content of those inputs to the behavior and outputs of the program.
Later we may start designing programs that themselves consist of multiple processes or threads that interact with one another. Because we can’t control when each process gets to use the CPU and for how long, we have only limited control on which of these threads will finish their respective tasks first. This leads to all kinds of unpredictable behaviors.
Why do we even bother, if non-determinism can introduce so many problems?
Well, for one thing, sometimes we actually value the unpredictability. Suppose you are playing a game against a computer opponent. How boring it is if the computer always makes exactly the same moves against you (even if you are repeating your own favorite sequence of moves). So game programmers often incorporate non-determinism or simulate it through the use of random number generators.
More often, however, we sometimes design programs to incorporate nondeterminism because the resulting designs are much, much, simpler. In my earlier example, we saw that, taking advantage of NFAs, it’s very easy to take the union of two languages. By contrast, if we had to do so without using NFAs, the procedure would have been actually quite similar to the subset construction that we use to convert an NFA to an FSA.
Now, the non-determinism that is provided by NFAs is a very limited form. It’s still an entirely predictable non-determinism. In fact, one might argue that an NFA is, despite its name, an entirely deterministic machine that we happen to view through a non-deterministic window. But that’s perfectly OK if it simplifies things for us. And, in the next chapter, NFAs will simplify things for us a lot!
1: There is a tiny, but non-zero, probability that all of air molecules in the room with you right now will suddenly hop outside the nearest door or window, leaving you gasping. — Just doing my bit to help you sleep at night!