Pushdown Automata: Examples
CS390, Spring 2024
Abstract
Practice running and constructing PDAs.
1 Automat
-
Review the Pushdown Automata section of the Automat help pages.
-
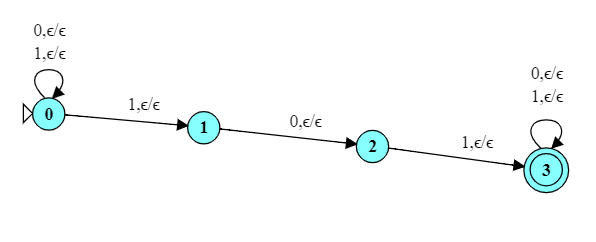
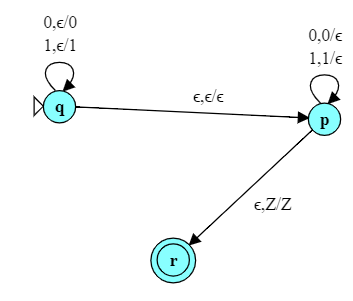
Here is the PDA for $0^n1^n$.
Try running it on these inputs:
- 0
- 1
- 01
- 10
- 0011
- 000111
- 00110
-
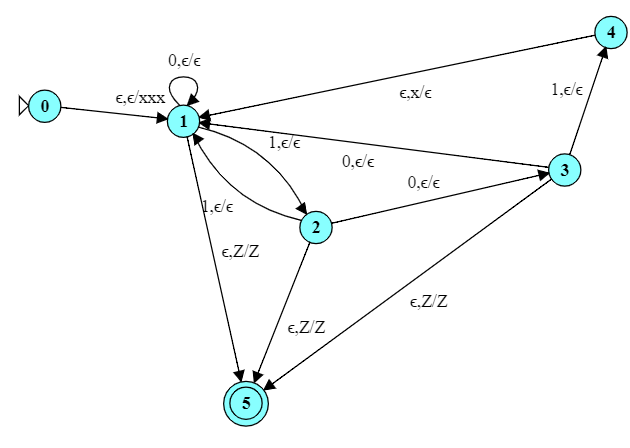
Here is the PDA for $ww^R$.
Try running it on these inputs:
- 0
- 1
- 00
- 0101
- 0110
- 10101
- 011001
- 111111
- 01100110
Take particular note of how some states can be active with many different stack contents. This is a new consequence of the nondeterminism in these automata.
-
A palindrome is a string that reads the same backwards as forwards. All strings in our $ww^R$ language are palindromes. But “1001001” is also a palindrome, and is not in $ww^R$.
Can you modify the $ww^R$ PDA so that it recognizes all palindromes over $\{0, 1\}^*$? (This is a good way to see if you have really embraced thinking about non-determinism.)
Try it before looking at the answer.
2 Sample Problems
2.1 A PDA can do anything a FA can.
I introduced PDAs by suggesting that they paired an NFA “controller” with a stack.
Because the controller is an NFA, it can recognize regular languages without even using the stack.
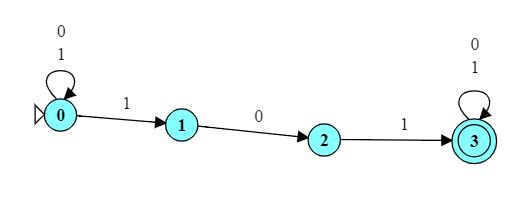
- Here is the NFA we used, weeks ago, to recognize the set of all strings over ${0, 1}$ that contain 101.
-
You might try running this on inputs 00100 and 001011 to refresh your memory of how it works.
With that as a guide, can you create a PDA to recognize the same language?
Reveal -
In general, any regular language can be recognized by a PDA constructed this way.
2.2 PDAs are good at counting.
FAs can recognize all regular languages, but sometimes PDAs can do it “better”.
Sometimes the stack can actually help. For example, PDAs are very good at counting things.
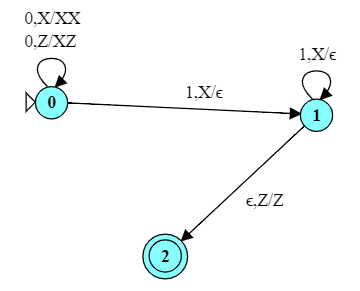
Consider the problem of designing an automaton to recognize strings with k occurrences of 101, where k is some constant.
-
Consider the language of strings over ${0, 1}$ that contain exactly three non-overlapping occurrences of 101.
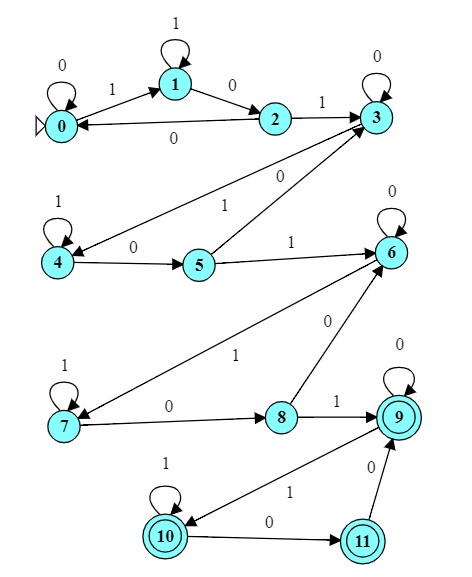
This is something that we can do with an FA.
- Try running this on 10101011101 and 10101011101101 to see how it works.
- The top “row” of states recognizes the first 101.
- The second row of states recognizes the second 101.
- The third row of states recognizes the first 101.
- The bottom row of states traps and rejects any string that has a fourth 101.
This is not the prettiest FA we’ve ever designed. In general, an FA to recognized exactly $k$ occurrences of a string of length $w$is going to require $O(k w)$ states.
Can you do this with a PDA, taking advantage of the stack to use fewer ($O(w)$) states?
RevealThis PDA could be very easily modified to look for two occurrences of 101, or five, or 100. Much easier than modifying the NFA.
- Try running this on 10101011101 and 10101011101101 to see how it works.
-
How would you modify the previous answer to accept strings with 5 occurrences of 101?
Reveal
2.3 PDAs are good at matching.
Another thing that PDAs are good at is matching/nesting combinations.
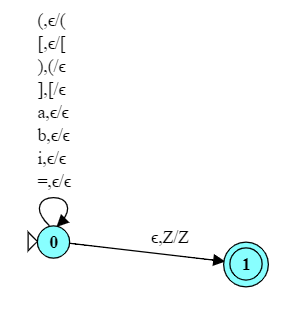
For example, consider the use of parentheses and brackets in C++ array expressions,
a[2*(i+1)] = (b[i] - 1)
- Design a PDA for a language over
{a, b, i, =, (, ) [, ] }to determine if the parentheses and brackets in such expressions are properly matched and nested.Reveal