Typing Mathematics (in Canvas)
CS390, Spring 2024
Abstract
In many of the quizzes and exams for this course, you will be typing mathematics. I will expect your mathematics to be both correct and readable. I will no more accept ugly scrawls for your mathematics than I would for your ordinary English text.
This lesson reviews a number of options that you have for typing readable mathematics, with an emphasis on how to do so in Canvas.
Let’s assume that you are in Canvas taking a quiz or test, or making a discussion board post, or working on an assignment. You are in the Canvas editor and discover that you need to do a bit of math, or maybe a lot of math.
You have options:
1 The Canvas Editor
If your expressions have nothing more complicated than superscripts and subscripts, e.g.,
\[ d_i = | x_i - x_0 | \]
you don’t need to leave the Canvas editor.
Just select the superscript or subscript text and use the super/subscript buttons to raise or lower the text. This works fine with things like x2 or xi.
It’s not as good when you need both superscripts and subscripts on the same expression. You can get x2i or xi2 this way, but neither looks quite as good as $x^2_i$.
 (video)
(video)2 HTML Entities
Sometimes you just need a special character or two. Beware of using your PC operating system’s character insertion utility. It may insert characters that look fine to you, but are invisible or look completely different to people viewing your work from other operating systems and/or other web browsers.
Instead, you can use the </> button to temporarily view and edit the raw HTML of your text, then type an HTML entity. An entity in HTML is a named character and is written with a leading ampersand (‘&’) and terminated with a semi-colon (‘;’).
 (video)
(video)Some useful entities in this course:
| Entity | Renders As | meaning |
|---|---|---|
α |
\(\alpha\) | alpha |
β |
\(\beta\) | beta |
γ |
\(\gamma\) | gamma |
δ |
\(\delta\) | delta |
ε |
\(\epsilon\) | epsilon, empty string |
&lamda; |
\(\lambda\) | lambda, “special” mark |
σ |
\(\sigma\) | sigma |
Σ |
\(\Sigma\) | upper-case sigma, alphabets |
≠ |
\(\neq\) | not equal to |
≤ |
\(\leq\) | less than or equal to |
≥ |
\(\geq\) | greater than or equal to |
→ |
\(\rightarrow\) | simple right arrow |
⇒ |
\(\Rightarrow\) | derives, implies |
∧ |
\(\wedge\) | logical and |
∨ |
\(\vee\) | logical or |
∈ |
\(\in\) | is in (set membership) |
∩ |
\(\cap\) | intersection |
∪ |
\(\cup\) | union |
⊂ |
\(\subset\) | is a proper subset of |
⊆ |
\(\subseteq\) | is a subset or equal to |
∀ |
\(\forall\) | for all |
∃ |
\(\exists\) | there exists |
𝒩 |
\(\cal{N}\) | natural numbers |
ℜ |
\(\cal{R}\) | real numbers |
3 The Math Editor
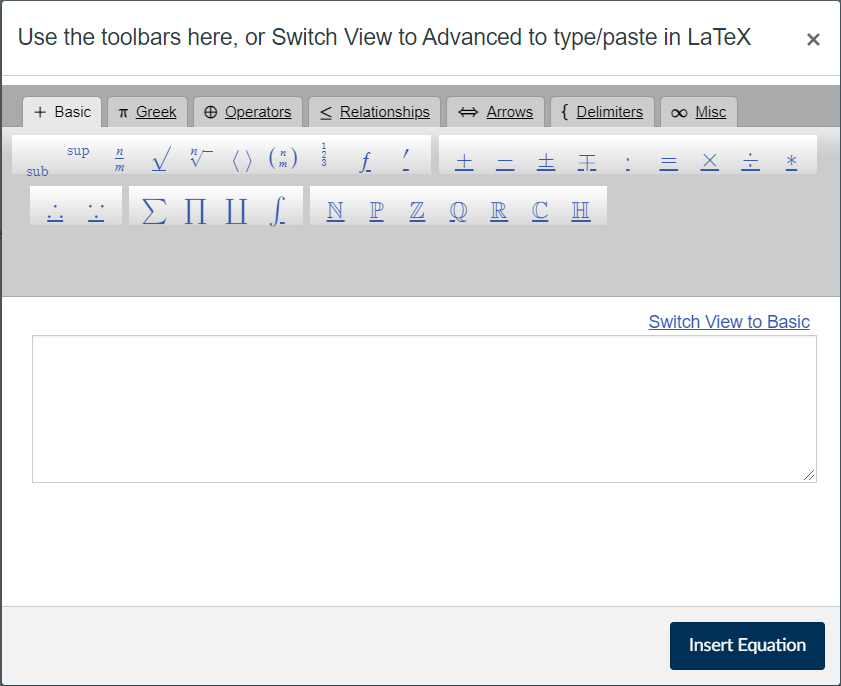
When you need more than a character or two, Canvas has a built-in equation editor, similar to the one found in most word processors. Click the $\sqrt{x}$ button to bring up a a window similar to the one shown on the right.
In that window you can compose mathematical expressions by simply clicking on the elements that you want. Some elements are “structured”, meaning that they will introduce additional text boxes that you can position your cursor within and add appropriate text.
 (video)
(video)Most math is actually a mixture of actual mathematics expressions and plain text explaining/discussing those expressions.
Never use the equation editor for plain text. Get in and out as you move back and forth from math to text. Typesetting plain text as if it were mathematics $often leads to a real mess$, because in mathematics, two characters next to each other represent a product of two variables (even if there is a space between them) and a math editor will typeset them accordingly.
4 LaTeX Mathematics
If you have a lot of math, particularly a derivation or a proof with multiple lines of mathematics that change just slightly from line to line, you may find the Canvas equation editor awkward because copy and pasting, then making slight alterations to the pasted expression, can be awkward.
A better option, once you get used to it, is to type your expression in LaTeX format. ..
4.1 TeX & LaTeX
TeX (pronounced “tech” - the ‘X’ is actually the Greek letter $\chi$.) is a typesetting program developed by the eminent computer scientist Donald Knuth. It was first released in 1978, well before word-processing had becom common-place.
LaTeX (pronounced “lah-tech”) was a popular package build on top of TeX to simplify document preparation. Although Canvas refers to it’s mathematics engine as supporting LaTeX, it really only employs the mathematics part of the full LaTeX definition, and that part comes more or less directly from TeX.
Even if you have no intention, however, of running the TeX program or any of its spin-offs (LaTeX, AMS-TeX, ConTeX,etc.), the TeX notation for mathematics stands as one of the best-known and most widely supported ways to type mathematics into a document for later automated typesetting. Although there has been considerable progress made since TeX’s introduction in rendering mathematics on the web, the focus there has been on the output side – the TeX notation is still the primary input format for advanced mathematics on the web and in professional publication.
4.2 TeX Fundamentals
4.2.1 Inline and Display Mode
Mathematics may be typeset in an inline fashion by placing the mathematics between \( and \). For example \( x+y\) yields $x + y$.
Mathematics may be typeset in a display fashion inside \[ and \], usually set off in a separate paragraph. So, if I type
\[ x = y + 1 \]
it is rendered as
\[ x = y + 1 \]
There are some mathematical expressions that will be rendered differently in inline and display mode. For example, the expression \(\sum_{i=1}^{n} x_i\) typesets as $\sum_{i=1}^{n} x_i$, but changing the outer markers, \[\sum_{i=1}^{n} x_i\] typesets as
\[ \sum_{i=1}^{n} x_i \]
positioning the summation limits differently based upon whether I surround the expressions with \(…\) or \[…\].
Both inline and display expressions can be typed across multiple lines, but will be grouped together as necessary. I can type, for example
\[ x =
y + 1 \]
and it will render as
\[x = y + 1 \]
When you enter TeX-style mathematics into Canvas, you have no choice. All math is treated as inline.
And you don’t type the surrounding chararaters
\(and\)or\[and\]: The Canvas editor will take care of that for you.
4.2.2 Special Characters
There are six special characters in TeX math expressions:
^is used to indicate a superscript. For examplex^2becomes $x^2$._is used to indicate a subscript. For examplex_ibecomes $x_i$.-
You might think, “Well, I can do that in HTML or in just about any rich text editor.” But consider the combination of the two, quite common in mathematics, such as
x_i^2, which renders properly as $x_i^2$, not as xi2.
-
-
The curly brackets
{and}are used for grouping mathematical expressions without introducing parentheses or other visible markers.Look at the difference between
x_i+1, rendering as $x_i+1$, andx_{i+1}, rendering as $x_{i+1}$. -
The
%is used to indicate that the rest of the line is a comment. For examplex + y = % addition is commutative y + xrenders as
\[ x + y = % addition is commutative y + x\]
-
Finally, the backslash
\indicates that characters are losing their “normal” meaning and taking on something new.For example, the “normal” meaning of
{and}is grouping, as shown above. But if we want to talk about sets, we can add a backslash:\{ x_{i,j} \}renders as $\{ x_{i,j} \}$.The most common use of
\will be to introduce “commands” for math that can’t be represented with a single character. This is often done together with{ }grouping. For example, $\sqrt{n}$ is typed as\sqrt{n}.
4.2.3 Basic Math
The arithmetic operators function much as you would expect: a * b + c / (d - e) renders as $a * b + c / (d - e)$.
One refinement is available for division. The \frac command typesets division in a vertical style:
\frac{a * b + c}{(d - e)} renders as $\frac{a * b + c}{(d - e)}$.
(Again, take note of the way that { } serve to group expressions together without contributing any visible characters to the final expression.)
 (video)
(video)4.3 Practice Exercises
Open this course in Canvas and go to the discussion “Typing Mathematics: Worksheet”.
Reply to the post there and try to reproduce each of the following expressions:
- $a^2$
- $a^2 + b^3$
- $x_{i-1}^2$
- $b^2 -4ac$
- $-b \pm \sqrt{b^2 -4ac}$
-
(Use
\pmfor the plus-or-minus and\sqrt{…}to get the square root.)
-
- $\frac{-b \pm \sqrt{b^2 -4ac}}{2a}$
- $x = \frac{-b \pm \sqrt{b^2 -4ac}}{2a}$
4.3.1 Boolean Operators
| LaTeX | Renders As | meaning |
|---|---|---|
x \wedge y |
$x \wedge y$ | and |
x \vee y |
$x \vee y$ | or |
\neg x |
$\neg x$ | not |
4.3.2 Relational Operators
| LaTeX | Renders As | meaning |
|---|---|---|
x < y |
$x < y$ | less than |
x > y |
$x > y$ | greater than |
x = y |
$x = y$ | equal to |
x \neq y |
$x \neq y$ | not equal to |
x \leq y |
$x \leq y$ | less than or equal to |
x \geq y |
$x \geq y$ | greater than |
A special note about the relational operators. If you are typing math into a program (_not_ Canvas!)designed to embed mathematics into HTML web pages, you may face a problem due to the face that “<” and “>” are reserved characters in HTML. In that case, you may find that you need to type them like this: x < y and x > y.
4.4 Making It Pretty
4.4.1 Making Things Bigger
Math symbols, particularly operators, can vary considerably in height. TeX has several “resizable” operators that not only tend to be taller than most characters, they can grow and shrink depending on context.
The most common of these are summation and product:
| LaTeX | Renders As | meaning |
|---|---|---|
\sum_i^n x_i |
$\sum_i^n x_i$ | summation |
\prod_i^n x_i |
$\prod_i^n x_i$ | product |
When you start writing large operators and vertical fractions into longer expression, the parentheses and grouping characters can start to look a little wimpy. For example
\sum_{i=0}^n (x_i + i) = (\sum_{i=0}^n x_i) + (\sum_{i=0}^n i) = (n \bar{x}) + (\frac{n(n+1)}{2})
\[ \sum_{i=0}^n (x_i + i) = (\sum_{i=0}^n x_i) + (\sum_{i=0}^n i) = (n \bar{x}) + (\frac{n(n+1)}{2}) \]
The parentheses in the above example look pretty awful. What we have is mathematically correct, but it’s not pretty.
You can request resizable parentheses or brackets by putting \left and \right in front of them.
\sum_{i=0}^n (x_i + i) = \left(\sum_{i=0}^n x_i \right) + \left(\sum_{i=0}^n i\right) = (n \bar{x}) + \left(\frac{n(n+1)}{2}\right)
\[ \sum_{i=0}^n (x_i + i) = \left(\sum_{i=0}^n x_i \right) + \left(\sum_{i=0}^n i\right) = (n \bar{x}) + \left(\frac{n(n+1)}{2}\right) \]
which certainly looks a lot better.
Every \left should be followed by a \right, though the brackets don’t have to match. \left(0, 10\right], rendering as $\left(0, 10\right]$, is perfectly legal.
If you want to have a left or right bracket that appears to be unmatched, you can use ‘.’ as the bracket character.
That’s how we get expressions like
\[ i(n) = \left\{ \begin{array}{ll} n/2 & \mbox{if n is even} \\
(-n-1) & \mbox{if n is odd} \\ \end{array} \right. \]
but we need a few more tricks before we can write all of that.
4.4.2 Text inside Mathematics
Let’s look at that line “n/2 if n is even” all by itself. If we do that as math:
n/2 if n is even
we get a mess:
\[ n/2 if n is even \]
That’s because, normally, when we write characters next to one another in mathematics, we mean them to represent the product of those single-character variables. Even just the word “if”, entered in math as if, will be rendered as $if$, because TeX assumes that by “if” we really mean “$i$ multiplied by $f$”.
Even when you put spaces inside your expression, the typesetter swallows those up in order to show what it thinks you meant by that expression.
If we need to put normal text words inside mathematics, there’s a special command, \mbox, used to indicate that something is actually text. In most LaTeX systems, you can also use \text.
n/2 \mbox{ if n is even}
or
n/2 \text{ if n is even}
\[ n/2 \mbox{ if n is even} \]
4.4.3 Arrays
You can arrange things into array-like structures with the array environment:
- Start with
\begin{array}and end with\end{array}. - Just after
\begin{array}, you indicate the number of coluns you need and whether the elements in each column should be left-justified, centered, or right-justified by a list of ‘l’, ‘c’, and ‘r’ characters. - In between the
\begin{array}and end with\end{array}, type your entries, separating entries within the same row by&and separatign the rows with\\.
So, for example,
\begin{array}{ll}
a & b \\
c & d \\
\end{array}
produces
\[ \begin{array}{ll} a & b \\ c & d \\ \end{array} \]
If that array looks a bit naked, we can give it some surrounding structure using the resizable bracketing we saw earlier:
\left|
\begin{array}{ll}
a & b \\
c & d \\
\end{array}
\right|
produces
\[ \left| \begin{array}{ll} a & b \\ c & d \\ \end{array} \right| \]
and
\left[
\begin{array}{ll}
a & b \\
c & d \\
\end{array}
\right]
produces
\[ \left[ \begin{array}{ll} a & b \\ c & d \\ \end{array} \right] \]
Returning to an earlier example
\begin{array}{ll}
n/2 & \mbox{if n is even} \\
(-n-1) & \mbox{if n is odd} \\
\end{array}
yields
\[ \begin{array}{ll} n/2 & \mbox{if n is even} \\ (-n-1) & \mbox{if n is odd} \\ \end{array} \]
We can then put a large { on the left and a large “nothing” on the right:
\left\\{ \begin{array}{ll}
n/2 & \mbox{if n is even} \\
(-n-1) & \mbox{if n is odd} \\
\end{array} \right.
yielding
\[ \left\{ \begin{array}{ll} n/2 & \mbox{if n is even} \\ (-n-1) & \mbox{if n is odd} \\ \end{array} \right. \]
And, finally, we can produce that full conditional expression I mentioned earlier:
i(n) = \left\{ \begin{array}{ll}
n/2 & \mbox{if n is even} \\
(-n-1) & \mbox{if n is odd} \\
\end{array} \right.
yielding
\[ i(n) = \left\{ \begin{array}{ll} n/2 & \mbox{if n is even} \\ (-n-1) & \mbox{if n is odd} \\ \end{array} \right. \]
4.4.4 Dots
An ellipsis is a mark used to show that something has been omitted. The most common form of ellipsis is denoted by three periods arranged horizontally. In TeX, this is formed by \ldots:
The natural numbers are \( 0, 1, 2, \ldots\)
renders as “The natural numbers are $0, 1, 2, \ldots$”.
Within arrays, however, we can use \vdots and \ddots to suggest missing elements in a vertical or a diagonal (combined horizontal and vertical) direction.
\left[\begin{array}{llll}
1 & 0 & \ldots & 0 \\
0 & 1 & \ldots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \ldots & 1 \\
\end{array}\right]
renders as
\[ \left[\begin{array}{llll} 1 & 0 & \ldots & 0 \\ 0 & 1 & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & 1 \\ \end{array}\right] \]
4.5 Try It Out
Open this course in Canvas and go to the discussion “Typing Mathematics: Worksheet”.
Reply to the post there and try to reproduce each of the following expressions:
- $S \cap T$
- $\{\epsilon, 0, 1, 00, 01, \ldots \}$
- $\bigcup_i S_i$
- $\left| \begin{array}{lll} X & X & O \\ O & X & \\ & O & X \\ \end{array} \right|$
(From https://xkcd.com/2586/)


