(Un)Decidability -- Sample Problems
CS390, Spring 2025
Abstract
This is a series of problems on the use of Turing Machines to explore decidability.
Try to solve each problem on your own, before revealing the solution.
1 Proof by Construction
Some problems, usually ones that ask you to prove a positive result, are done describing the construction of a TM to solve a desired problem.
1.1 Does it Move?
We’ve discussed the common variant of allowing Turing Machines an option of keeping the head in the same place after a transition instead of always moving one space to the left or right.
Let fixed(T) be the property that one of these extended Turing machines T never moves its head to the left or to the right, on any input that it accepts.
Prove that this property is recursive.
Note: You cannot do this simply by inspecting the finite state control of the TM and seeing whether it has any transitions marked L or R. You have to consider the possibility that any such transitions might not actually be triggered by any possible input.
1.2 The Bounded UTM
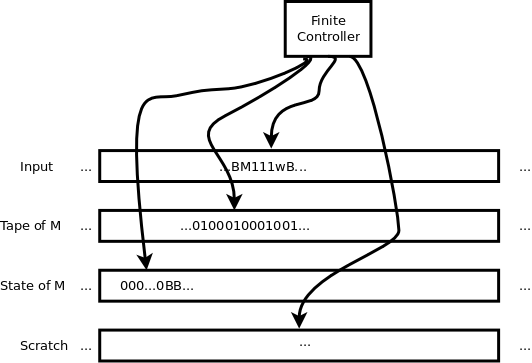
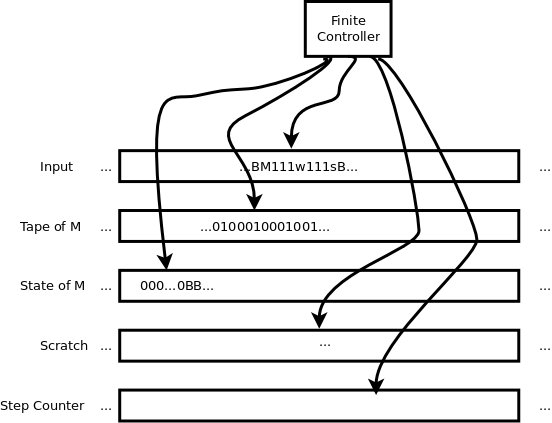
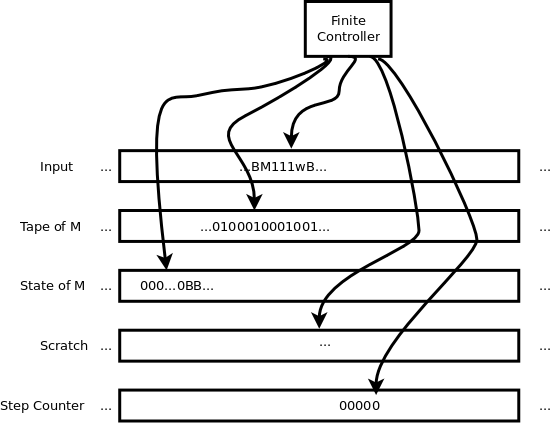
A Universal Turing machine (UTM) accepts a code for a Turing machine M and a string w, encoded as M111w.
Now consider a variation on the UTM that accepts input of the form M111w111s, where s is an integer (in unary form, a string of zeros) representing a number of steps. Can you construct a TM, a “bounded UTM”, that accepts strings of that form if and only if the TM M accepts the input w in s or fewer steps?
2 Reductions
Negative results, showing that a problem P is not recursive or not RE, are often achieved by reducing a known non-recursive or non-RE problem to P, so that if P could be solved, then the other problem would be solved as well, thereby raising a contradiction.
2.1 The Halting Problem is not Recursive
The halting problem is the problem of determining, given a pair (T,w) consisting of a Turing machine T and a string w, whether T halts when presented w as input, regardless of whether T accepts w or not.
Prove that the halting problem is not recursive i.e., there is no algorithm that can determine whether an arbitrary T halts on an arbitrary w.
2.2 The Halting Problem is RE
The previous problem establishes that we cannot decide whether a TM halts on a given input. Now consider the weaker problem of whether we can list (given infinite time) the (T,w) pairs such that T halts on input w.
Prove that the halting problem is recursively enumerable, i.e., there is a Turing machine that enumerates all such (T,w) pairs.
2.3 Halting on empty input
Many problems can be proven by reduction to the halting problem.
For example, is it decidable whether an arbitrary Turing machine halts when presented with an empty input tape?
3 Rice’s Theorem
Rice’s theorem is a powerful tool for proving negative results about sets of languages.
Rice’s Theorem states that all non-trivial properties of the RE languages are undecidable.
To use it we must do two things:
-
Express the problem as a property of the RE languages.
-
Show that the property is not trivial: the set is neither empty nor universal.
Try to use Rice’s theorem to answer the following:
3.1 Accepting an Infinite Number of Strings
Is it decidable whether an arbitrary TM accepts an infinite number of strings?
3.2 Accepting 1011
Is it decidable whether an arbitrary TM accepts a particular input, e.g., 1011?
3.3 Accepting All Strings Over its Alphabet
Is it decidable whether an arbitrary TM over alphabet Σ accepts all strings in Σ∗?
3.4 Never Moving Far
Is it decidable whether an arbitrary TM never moves more than 2 steps to the left or right of its starting position?