1.2).    Using Venn Diagrams verify each of the set Identities. (Text Book Excercises)

           Some of the important from the 19 set identities are solved here and the rest are left
           for you.

    Solution:
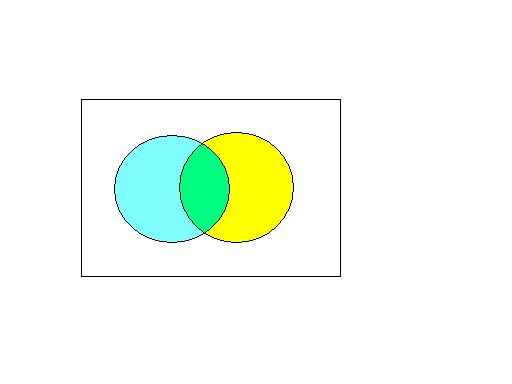
          Note: Green color is the intersection region for yellow and blue when using
                      yellow for one set and blue for other. When illustrating using three sets
                     red, blue, green are used for different  sets and black is used for the
                     intersection of all three.

            i)    A  B = B  A

                  The below shown are the individual sets A and B

                Assuming that there are some elements which belong to and some elements which belong
                to B and some elements which belong to both A and B. Then A  B is as shown below.

               The whole of the region consisting of yellow, green and blue alltogether is A  B.

                Now let us do the same for B  A.

                B  A is the region consisting of yellow, green and blue.
                As both A  B and B  A cover the same region shown by pink,

                we can conclude that

                                           A  B = B  A
 

        2)    A  ( A   B)  =  A
                    First let us draw the Venn diagram of A  B and then the complete Venn Diagram for
              A  ( A   B)

                Venn Diagram for A   B is shown below
                Green color portion is the A  B area.

              Now let us draw the Venn Diagram for A  ( A   B)

              From the above Venn Diagram it should be very clear that A  ( A   B)  is A.
                According to the definition of  Union, the area belonging to only A and area
                belonging to only B and the area common for both A and B is the area which
                belongs to A   B. So from the above Venn diagrams it is pretty clear that
                the green portion showing A   B is a part of A and so the answer is A itself.

           3)     (A  B)' = A'  B'
                  Let us complete the Venn Diagram for (A  B)'. Then complete the Venn Diagram
                    for A'  B' and compare to see if they both cover the same area of the Venn Diagrams,
                    if so the identity is proved.
                   As a first step, we will start with drawing Venn Diagram for  (A  B)'.
                   (A  B)' Venn Diagram is shown below

                                                                fig. 1
                    Blue color area indicates (A  B)'. It is the area belonging to  U - (A  B).
                  Now let us draw the Venn Diagram for A' and B' and then their intersection.

                    Yellow region indicates the A' area and blue color indicates the B' area..

                                                                    Fig. 2
                    B' is shown below.

                                                                      Fig 3

                    The intersection of above two Venn Diagrams is nothing but the common area
                    covered by both the Venns. It is nothing but A'  B' shown below
                                                                        Fig. 4

                                                                A'  B' area.

                    By observing the area covered in both Fig.1 and Fig.4 we can say that both
                   (A  B)'  and  A'  B'  cover the same area. So the identity is proved.
 

           4)    A  A' =  Null (empty set)

                    Set A and A' are shown in the following Venn Diagram.

                    The following is the Venn Diagram for    A  A'

                    From fig.1 we can clearly see that there is nothin in common between A and A'.
                    Intersection implies the elements common in both the sets. As the sets have no
                    common elements(area) its an Empty Set or NULL set.