Context-Free Languages
Context-Free Grammar
Subjects to be Learned
- Context-Free Grammar
- Context-Free Languages
- Push Down Automata
Contents
Earlier in the discussion of grammars we saw context-free grammars.
They are grammars whose productions have the form
X ->  , where X is a nonterminal and
, where X is a nonterminal and
 is a nonempty string of terminals
and nonterminals.
The set of strings generated by a context-free grammar is called a context-free
language and context-free languages can describe many practically important
systems. Most programming languages can be approximated by context-free grammar
and compilers for them have been developed based on properties of context-free
languages. Let us define context-free
grammars and context-free languages here.
is a nonempty string of terminals
and nonterminals.
The set of strings generated by a context-free grammar is called a context-free
language and context-free languages can describe many practically important
systems. Most programming languages can be approximated by context-free grammar
and compilers for them have been developed based on properties of context-free
languages. Let us define context-free
grammars and context-free languages here.
Definition (Context-Free Grammar) :
A 4-tuple G = < V ,  , S , P >
is a context-free grammar (CFG) if
V and
, S , P >
is a context-free grammar (CFG) if
V and  are finite sets sharing no elements
between them, S
are finite sets sharing no elements
between them, S  V is the start
symbol, and P is a finite set of productions of the form X ->
V is the start
symbol, and P is a finite set of productions of the form X ->
 , where
X
, where
X  V , and
V , and

 ( V
( V 
 )* .
)* .
A language is a context-free language (CFL)
if all of its strings are generated by a context-free grammar.
Example 1:
L1 = { anbn | n is a positive integer }
is a context-free language. For the following context-free grammar
G1 = < V1 ,  , S ,
P1 > generates L1 :
, S ,
P1 > generates L1 :
V1 = { S } ,  = { a , b } and
P1 = { S -> aSb , S -> ab }.
= { a , b } and
P1 = { S -> aSb , S -> ab }.
Example 2:
L2 = { wwr| w  {a, b }+ } is a context-free language ,
where w is a non-empty string and wr denotes the reversal of string w,
that is, w is spelled backward to obtain wr . For the following
context-free grammar
G2 = < V2 ,
{a, b }+ } is a context-free language ,
where w is a non-empty string and wr denotes the reversal of string w,
that is, w is spelled backward to obtain wr . For the following
context-free grammar
G2 = < V2 ,  , S ,
P2 >
generates L2 :
, S ,
P2 >
generates L2 :
V2 = { S } ,  = { a , b } and
P2 = { S -> aSa , S -> bSb , S -> aa , S -> bb }.
= { a , b } and
P2 = { S -> aSa , S -> bSb , S -> aa , S -> bb }.
Example 3:
Let L3 be the set of algebraic expressions involving identifiers x and y,
operations + and * and left and right parentheses. Then L3 is a context-free
language.
For the following context-free grammar
G3 = < V3 ,  3, S ,
P3 > generates L3 :
3, S ,
P3 > generates L3 :
V3 = { S } ,  3
= { x , y , ( , ) , + , * } and
P3 = { S -> ( S + S ) , S -> S*S , S -> x , S -> y }.
3
= { x , y , ( , ) , + , * } and
P3 = { S -> ( S + S ) , S -> S*S , S -> x , S -> y }.
Example 4:
Portions of the syntaxes of programming languages can be described by context-free
grammars. For example
{ < statement > -> < if-statement > , < statement > -> <
for-statement > ,
< statement > -> < assignment > , . . . ,
< if-statement > -> if ( < expression > ) < statement > ,
< for-statement > -> for ( < expression > ; < expression >
; < expression > )
< statement > , . . . , < expression > -> < algebraic-expression > ,
< expression >
-> < logical-expression > , . . . } .
Properties of Context-Free Language
Theorem 1:
Let L1 and L2 be context-free languages.
Then L1  L2 , L1L2 ,
and L1* are context-free languages.
L2 , L1L2 ,
and L1* are context-free languages.
Outline of Proof
This theorem can be verified by constructing context-free grammars
for union, concatenation and Kleene star of context-free grammars as follows:
Let G1 = < V1 ,  ,
S1 , P1 > and G2 = < V2 ,
,
S1 , P1 > and G2 = < V2 ,
 ,
S2 , P2 > be context-free grammars generating L1 and
L2 , respectively.
,
S2 , P2 > be context-free grammars generating L1 and
L2 , respectively.
Then for L1  L2 , first relabel symbols
of V2 , if necessary, so that V1 and V2 don't share any
symbols. Then let Su be a symbol
which is not in V1
L2 , first relabel symbols
of V2 , if necessary, so that V1 and V2 don't share any
symbols. Then let Su be a symbol
which is not in V1  V2 .
Next define Vu = V1
V2 .
Next define Vu = V1  V2
V2
 { Su } and
Pu = P1
{ Su } and
Pu = P1  P2
P2
 { Su -> S1 ,
Su -> S2 } .
{ Su -> S1 ,
Su -> S2 } .
Then it can be easily seen that Gu = < Vu ,
 ,
Su , Pu > is a context-free grammar that generates the language
L1
,
Su , Pu > is a context-free grammar that generates the language
L1  L2 .
L2 .
Similarly for L1L2 , first relabel symbols of V2 ,
if necessary, so that V1 and V2 don't share any symbols.
Then let Sc be a symbol
which is not in V1  V2 .
Next define Vc = V1
V2 .
Next define Vc = V1  V2
V2
 { Sc } and
Pc = P1
{ Sc } and
Pc = P1  P2
P2
 { Sc -> S1S2 } .
{ Sc -> S1S2 } .
Then it can be easily seen that Gc = < Vc ,
 ,
Sc , Pc > is a context-free grammar that generates the language
L1L2 .
,
Sc , Pc > is a context-free grammar that generates the language
L1L2 .
For L1* , let Ss be a symbol
which is not in V1 . Then let Ps = P1
 { Ss -> SsS1 ,
Ss ->
{ Ss -> SsS1 ,
Ss ->  } .
It can be seen that the grammar Gs = < Vs ,
} .
It can be seen that the grammar Gs = < Vs ,
 ,
Ss , Ps > is a context-free grammar that generates the language
L1* .
,
Ss , Ps > is a context-free grammar that generates the language
L1* .
Pushdown Automata
Like regular languages which are accepted by finite automata, context-free
languages are also accepted by automata but not finite automata. They need a little more
complex automata called pushdown automata.
Let us consider a context-free language anbn .
Any string of this language can be tested for the membership for the language
by a finite automaton if there is a memory such as a pushdown stack that can store
a's of a given input string. For example, as a's are read by the finite
automaton,
push them into the stack.
As soon as the symbol b appears stop storing a's and start popping a's one
by one every time a b is read.
If another a (or anything other than b) is read after the first b, reject the string.
When all the symbols of the input string are read, check the stack.
If it is empty, accept the string. Otherwise reject it.
This automaton behaves like a finite automaton except the following two points: First,
its next state is determined not only by the input symbol being read, but also
by the symbol at the top of the stack. Second, the contents of the stack can also
be changed
every time an input symbol is read. Thus its transition function specifies the new top of
the stack contents as well as the next state.
Let us define this new type of automaton formally.
A pushdown automaton ( or PDA for short )
is a 7-tuple M = < Q ,  ,
,
 , q0 , Z0 , A ,
, q0 , Z0 , A ,
 > , where
> , where
Q is a finite set of states,
 and
and
 are finite sets ( the input and stack alphabet, respectively ).
are finite sets ( the input and stack alphabet, respectively ).
q0 is the initial state,
Z0 is the initial stack symbol and it is a member of  ,
,
A is the set of accepting states
 is the transition function and
is the transition function and
 : Q
: Q 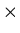 (
(
 (
( }
}
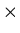
 -> 2 Q
-> 2 Q
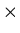
 *.
*.
Thus  ( p , a , X ) =
( q ,
( p , a , X ) =
( q ,  ) means the following:
) means the following:
The automaton moves from the current
state of p to the next state q when it sees an input symbol a at the input and X at the top
of the stack, and it replaces X with the string  at the top of the stack.
at the top of the stack.
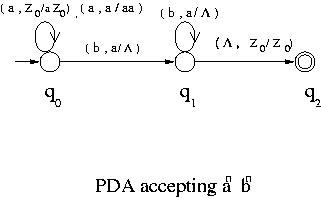
Example 1 :
Let us consider the pushdown automaton < Q ,  ,
,
 , q0 , Z0 , A ,
, q0 , Z0 , A ,
 > , where
Q = { q0 , q1 , q2 } ,
> , where
Q = { q0 , q1 , q2 } ,
 = { a , b } ,
= { a , b } ,
 = { a , b , Z0 } ,
A = { q2 } and let
= { a , b , Z0 } ,
A = { q2 } and let  be as given in the following
table:
be as given in the following
table:
| State | Input | Top of Stack | Move |
| q0 | a | Z0 | ( q0 , aZ 0 ) |
| q0 | a | a | ( q0 , aa ) |
| q0 | b | a | ( q1 ,  ) ) |
| q1 | b | a | ( q1 ,  ) ) |
| q1 |  | Z0 | ( q2 , Z0 ) |
This pushdown automaton accepts the language anbn .
To describe the operation of a PDA we are going to use a configuration of PDA.
A configuration of a PDA M = < Q ,
 ,
,
 , q0 , Z0 , A ,
, q0 , Z0 , A ,
 > is a triple
( q , x ,
> is a triple
( q , x ,  ) , where q is the state the PDA is currently in,
x is the unread portion of the input string and
) , where q is the state the PDA is currently in,
x is the unread portion of the input string and  is the current stack contents, where the input is read from left to right
and the top of the stack corresponds to the leftmost symbol of
is the current stack contents, where the input is read from left to right
and the top of the stack corresponds to the leftmost symbol of
 . To express that the PDA moves from
configuration ( p , x ,
. To express that the PDA moves from
configuration ( p , x ,  ) to configuration
( q , y ,
) to configuration
( q , y , 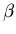 ) in a single move
(a single application of the transition function)
we write
) in a single move
(a single application of the transition function)
we write
( p , x ,  )
)
 ( q , y ,
( q , y , 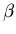 ) .
) .
If ( q , y , 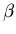 ) is reached from
( p , x ,
) is reached from
( p , x ,  ) by a sequence of zero or more moves,
we write
) by a sequence of zero or more moves,
we write
( p , x ,  )
)
 *
( q , y ,
*
( q , y , 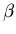 ) .
) .
Let us now see how the PDA of Example 1 operates when it is given the string aabb ,
for example.
Initially its configuration is ( q0 , aabb , Z0 ).
After reading the first a, its configuration is ( q0 , abb , aZ0 ).
After reading the second a, it is ( q0 , bb , aaZ0 ).
Then when the first b is read, it moves to state
q1 and pops a from the top of the stack. Thus the configuration is
( q1 , b , aZ0 ). When the second b is read, another a is
popped from the top of the stack and the PDA stays in state q1 .
Thus the configuration is ( q1 ,  ,
Z0 ). Next it moves to the state q2 which is the accepting state.
Thus aabb is accepted by this PDA. This entire process can be expressed using
the configurations as
,
Z0 ). Next it moves to the state q2 which is the accepting state.
Thus aabb is accepted by this PDA. This entire process can be expressed using
the configurations as
( q0 , aabb , Z0 )  ( q0 , abb , aZ0 )
( q0 , abb , aZ0 )  ( q0 , bb , aaZ0 )
( q0 , bb , aaZ0 )  ( q1 , b , aZ0 )
( q1 , b , aZ0 )  ( q1 ,
( q1 ,  , Z0 )
, Z0 )
 ( q2 ,
( q2 ,  , Z0 ).
, Z0 ).
If we are not interested in the intermediate steps, we can also write
( q0 , aabb , Z0 )  *
( q2 ,
*
( q2 ,  , Z0 ) .
, Z0 ) .
A string x is accepted by a PDA
(a.k.a. acceptance by final state) if
(q0, x, Z0)  *
(q,
*
(q,  ,
,  ), for some
), for some
 in
in  *, and
an accepting state q.
*, and
an accepting state q.
Like FAs, PDAs can also be represented by transition diagrams. For PDAs, however,
arcs are labeled differently than FAs. If  ( q , a , X ) =
( p ,
( q , a , X ) =
( p ,  ) , then an arc from state p to state q is added to
the diagram and it is labeled with ( a , X /
) , then an arc from state p to state q is added to
the diagram and it is labeled with ( a , X /  )
indicating that X at the top of the stack is replaced by
)
indicating that X at the top of the stack is replaced by  upon reading a from the input.
For example the transition diagram of the PDA of Example 1 is as shown below.
upon reading a from the input.
For example the transition diagram of the PDA of Example 1 is as shown below.
Example 2 :
Let us consider the pushdown automaton < Q ,  ,
,
 , q0 , Z0 , A ,
, q0 , Z0 , A ,
 > , where
Q = { q0 , q1 , q2 } ,
> , where
Q = { q0 , q1 , q2 } ,  = { a , b , c } ,
= { a , b , c } ,  =
{ a , b , Z0 } , A = { q2 } and let
=
{ a , b , Z0 } , A = { q2 } and let  be as given in the following table:
be as given in the following table:
| State | Input | Top of Stack | Move |
| q0 | a | Z0 | ( q0 , aZ 0 ) |
| q0 | b | Z0 | ( q0 , bZ 0 ) |
| q0 | a | 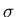 | ( q0 , a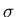 ) ) |
| q0 | b | 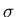 | ( q0 , b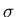 ) ) |
| q0 | c | 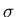 | ( q1 , 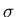 ) ) |
| q1 | a | a | ( q1 ,  ) ) |
| q1 | b | b | ( q1 ,  ) ) |
| q1 |  | Z0 | ( q2 , Z0 ) |
In this table 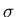 represents either a or b.
represents either a or b.
This pushdown automaton accepts the language { wcwr | w
 { a , b }* } , which is
the set of palindromes with c in the middle.
{ a , b }* } , which is
the set of palindromes with c in the middle.
For example for the input abbcbba, it goes through the following configurations and
accepts it.
( q0 , abbcbba , Z0 )  ( q0 , bbcbba , aZ0 )
( q0 , bbcbba , aZ0 )  ( q0 , bcbba , baZ0 )
( q0 , bcbba , baZ0 )  ( q0 , cbba , bbaZ0 )
( q0 , cbba , bbaZ0 )
 ( q1 , bba , bbaZ0 )
( q1 , bba , bbaZ0 )  ( q1 , ba , baZ0 )
( q1 , ba , baZ0 )  ( q1 , a , aZ0 )
( q1 , a , aZ0 )  ( q1 ,
( q1 ,  , Z0 )
, Z0 )
 ( q2 ,
( q2 ,  , Z0 ) .
, Z0 ) .
This PDA pushes all the a's and b's in the input into stack until c is encountered.
When c is detected, it ignores c and from that point on
if the top of the stack matches the input symbol, it pops the stack.
When there are no more unread input symbols and Z0 is at the top of the stack,
it accepts the input string. Otherwise it rejects the input string.
The transition diagram of the PDA of Example 2 is as shown below.
In the figure 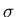 ,
,
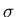 1 and
1 and
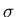 2 represent a or b.
2 represent a or b.

Further topics on CFL
- PDA and Context-Free Language
There is a procedure to construct a PDA that accepts the language generated by
a given context-free grammar and conversely.
That means that a language is context-free if and only if there is a PDA
that accepts it. Those procedures are omitted here.
- Pumping Lemma for Context-Free Language
Let L be a CFL. Then there is a positive integer n such that for any string u in L
with |u| 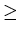 n , there are strings
v, w, x, y and z which satisfy
n , there are strings
v, w, x, y and z which satisfy
u = vwxyz
|wy| > 0
|wxy| 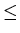 n
n
for every integer m 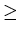 0 ,
vwmxymz
0 ,
vwmxymz  L
L
- Parsing and Parsers for CFL
Consider the algebraic expression x + yz. Though we are accustomed to interpreting
this as x + (yz) i.e. compute yz first, then add the result to x, it could also be
interpreted as ( x + y )z meaning that first compute x + y, then multiply the result
by z. Thus if a computer is given the string x + yz, it does not know which
interpretation to use unless it is explicitly instructed to follow one or the other.
Similar things happen when English sentences are processed by computers (or people
as well for that matter). For example in the sentence "A man bites a dog", native
English speakers know that it is the dog that bites and not the other way round.
"A dog" is the subject, "bites" is the verb and "a man" is the object of the verb.
However, a computer like non-English speaking people must be told how to interpret
sentences such as the first noun phrase (" A dog") is usually the subject
of a sentence, a verb phrase usually follow the noun phrase and the first word
in the verb phrase is the verb and it is followed by noun phrases reprtesenting
object(s) of the verb.
Parsing is the process of interpreting given input strings according to predetermined
rules i.e. productions of grammars. By parsing sentences we identify the parts of the
sentences and
determine the strutures of the sentences so that their meanings can be understood
correctly.
Contect-free grammars are powerful grammars. They can describe much of programming
languages and basic structures of natural languages. Thus they are widely used
for compilers for high level programming languages and natural language processing systems.
The parsing for context-free languages and regular languages have been extensively
studied. However, we are not going to study parsing here. Interested readers are
referred to the textbook and other sources.
????
references on Parsing
????
Test Your Understanding of Contect-Free Language
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.
Next -- Turing Machines
Back to Schedule
Back to Table of Contents
 )
)  )
) 
 , where X is a nonterminal and
, where X is a nonterminal and
 is a nonempty string of terminals
and nonterminals.
The set of strings generated by a context-free grammar is called a context-free
language and context-free languages can describe many practically important
systems. Most programming languages can be approximated by context-free grammar
and compilers for them have been developed based on properties of context-free
languages. Let us define context-free
grammars and context-free languages here.
is a nonempty string of terminals
and nonterminals.
The set of strings generated by a context-free grammar is called a context-free
language and context-free languages can describe many practically important
systems. Most programming languages can be approximated by context-free grammar
and compilers for them have been developed based on properties of context-free
languages. Let us define context-free
grammars and context-free languages here.
 , S , P >
is a context-free grammar (CFG) if
V and
, S , P >
is a context-free grammar (CFG) if
V and  are finite sets sharing no elements
between them, S
are finite sets sharing no elements
between them, S  V is the start
symbol, and P is a finite set of productions of the form X ->
V is the start
symbol, and P is a finite set of productions of the form X ->
 , where
X
, where
X  V , and
V , and

 ( V
( V 
 )* .
)* .
 , S ,
P1 > generates L1 :
, S ,
P1 > generates L1 :
 = { a , b } and
P1 = { S -> aSb , S -> ab }.
= { a , b } and
P1 = { S -> aSb , S -> ab }.
 {a, b }+ } is a context-free language ,
where w is a non-empty string and wr denotes the reversal of string w,
that is, w is spelled backward to obtain wr . For the following
context-free grammar
G2 = < V2 ,
{a, b }+ } is a context-free language ,
where w is a non-empty string and wr denotes the reversal of string w,
that is, w is spelled backward to obtain wr . For the following
context-free grammar
G2 = < V2 ,  , S ,
P2 >
generates L2 :
, S ,
P2 >
generates L2 :
 = { a , b } and
P2 = { S -> aSa , S -> bSb , S -> aa , S -> bb }.
= { a , b } and
P2 = { S -> aSa , S -> bSb , S -> aa , S -> bb }.
 3, S ,
P3 > generates L3 :
3, S ,
P3 > generates L3 :
 3
= { x , y , ( , ) , + , * } and
P3 = { S -> ( S + S ) , S -> S*S , S -> x , S -> y }.
3
= { x , y , ( , ) , + , * } and
P3 = { S -> ( S + S ) , S -> S*S , S -> x , S -> y }.
 L2 , L1L2 ,
and L1* are context-free languages.
L2 , L1L2 ,
and L1* are context-free languages.
 ,
S1 , P1 > and G2 = < V2 ,
,
S1 , P1 > and G2 = < V2 ,
 ,
S2 , P2 > be context-free grammars generating L1 and
L2 , respectively.
,
S2 , P2 > be context-free grammars generating L1 and
L2 , respectively.
 L2 , first relabel symbols
of V2 , if necessary, so that V1 and V2 don't share any
symbols. Then let Su be a symbol
which is not in V1
L2 , first relabel symbols
of V2 , if necessary, so that V1 and V2 don't share any
symbols. Then let Su be a symbol
which is not in V1  V2 .
Next define Vu = V1
V2 .
Next define Vu = V1  V2
V2
 { Su } and
Pu = P1
{ Su } and
Pu = P1  P2
P2
 { Su -> S1 ,
Su -> S2 } .
{ Su -> S1 ,
Su -> S2 } .
 ,
Su , Pu > is a context-free grammar that generates the language
L1
,
Su , Pu > is a context-free grammar that generates the language
L1  L2 .
L2 .
 V2 .
Next define Vc = V1
V2 .
Next define Vc = V1  V2
V2
 { Sc } and
Pc = P1
{ Sc } and
Pc = P1  P2
P2
 { Sc -> S1S2 } .
{ Sc -> S1S2 } .
 ,
Sc , Pc > is a context-free grammar that generates the language
L1L2 .
,
Sc , Pc > is a context-free grammar that generates the language
L1L2 .
 { Ss -> SsS1 ,
Ss ->
{ Ss -> SsS1 ,
Ss ->  } .
It can be seen that the grammar Gs = < Vs ,
} .
It can be seen that the grammar Gs = < Vs ,
 ,
Ss , Ps > is a context-free grammar that generates the language
L1* .
,
Ss , Ps > is a context-free grammar that generates the language
L1* .
 ,
,
 , q0 , Z0 , A ,
, q0 , Z0 , A ,
 > , where
> , where
 and
and
 are finite sets ( the input and stack alphabet, respectively ).
are finite sets ( the input and stack alphabet, respectively ).
 ,
,
 is the transition function and
is the transition function and
 : Q
: Q 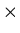 (
(
 (
( }
}
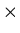
 -> 2 Q
-> 2 Q
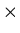
 *.
*.
 ( p , a , X ) =
( q ,
( p , a , X ) =
( q ,  ) means the following:
) means the following:
 at the top of the stack.
at the top of the stack.
 ,
,
 , q0 , Z0 , A ,
, q0 , Z0 , A ,
 > , where
Q = { q0 , q1 , q2 } ,
> , where
Q = { q0 , q1 , q2 } ,
 = { a , b } ,
= { a , b } ,
 = { a , b , Z0 } ,
A = { q2 } and let
= { a , b , Z0 } ,
A = { q2 } and let  be as given in the following
table:
be as given in the following
table:
 )
)  )
) 
 ,
,
 , q0 , Z0 , A ,
, q0 , Z0 , A ,
 > is a triple
( q , x ,
> is a triple
( q , x ,  ) , where q is the state the PDA is currently in,
x is the unread portion of the input string and
) , where q is the state the PDA is currently in,
x is the unread portion of the input string and  is the current stack contents, where the input is read from left to right
and the top of the stack corresponds to the leftmost symbol of
is the current stack contents, where the input is read from left to right
and the top of the stack corresponds to the leftmost symbol of
 . To express that the PDA moves from
configuration ( p , x ,
. To express that the PDA moves from
configuration ( p , x ,  ) to configuration
( q , y ,
) to configuration
( q , y , 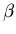 ) in a single move
(a single application of the transition function)
we write
) in a single move
(a single application of the transition function)
we write
 )
)
 ( q , y ,
( q , y , 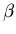 ) .
) .
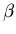 ) is reached from
( p , x ,
) is reached from
( p , x ,  ) by a sequence of zero or more moves,
we write
) by a sequence of zero or more moves,
we write
 )
)
 *
( q , y ,
*
( q , y , 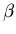 ) .
) .
 ,
Z0 ). Next it moves to the state q2 which is the accepting state.
Thus aabb is accepted by this PDA. This entire process can be expressed using
the configurations as
,
Z0 ). Next it moves to the state q2 which is the accepting state.
Thus aabb is accepted by this PDA. This entire process can be expressed using
the configurations as
 ( q0 , abb , aZ0 )
( q0 , abb , aZ0 )  ( q0 , bb , aaZ0 )
( q0 , bb , aaZ0 )  ( q1 , b , aZ0 )
( q1 , b , aZ0 )  ( q1 ,
( q1 ,  , Z0 )
, Z0 )
 ( q2 ,
( q2 ,  , Z0 ).
, Z0 ).
 *
( q2 ,
*
( q2 ,  , Z0 ) .
, Z0 ) .
 *
(q,
*
(q,  ,
,  ), for some
), for some
 in
in  *, and
an accepting state q.
*, and
an accepting state q.
 ( q , a , X ) =
( p ,
( q , a , X ) =
( p ,  ) , then an arc from state p to state q is added to
the diagram and it is labeled with ( a , X /
) , then an arc from state p to state q is added to
the diagram and it is labeled with ( a , X /  )
indicating that X at the top of the stack is replaced by
)
indicating that X at the top of the stack is replaced by  upon reading a from the input.
For example the transition diagram of the PDA of Example 1 is as shown below.
upon reading a from the input.
For example the transition diagram of the PDA of Example 1 is as shown below.

 ,
,
 , q0 , Z0 , A ,
, q0 , Z0 , A ,
 > , where
Q = { q0 , q1 , q2 } ,
> , where
Q = { q0 , q1 , q2 } ,  = { a , b , c } ,
= { a , b , c } ,  =
{ a , b , Z0 } , A = { q2 } and let
=
{ a , b , Z0 } , A = { q2 } and let  be as given in the following table:
be as given in the following table:
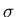
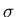 )
) 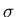
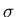 )
) 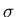
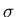 )
)  )
)  )
) 
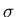 represents either a or b.
represents either a or b.
 { a , b }* } , which is
the set of palindromes with c in the middle.
{ a , b }* } , which is
the set of palindromes with c in the middle.
 ( q0 , bbcbba , aZ0 )
( q0 , bbcbba , aZ0 )  ( q0 , bcbba , baZ0 )
( q0 , bcbba , baZ0 )  ( q0 , cbba , bbaZ0 )
( q0 , cbba , bbaZ0 )
 ( q1 , bba , bbaZ0 )
( q1 , bba , bbaZ0 )  ( q1 , ba , baZ0 )
( q1 , ba , baZ0 )  ( q1 , a , aZ0 )
( q1 , a , aZ0 )  ( q1 ,
( q1 ,  , Z0 )
, Z0 )
 ( q2 ,
( q2 ,  , Z0 ) .
, Z0 ) .
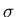 ,
,
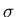 1 and
1 and
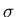 2 represent a or b.
2 represent a or b.

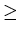 n , there are strings
v, w, x, y and z which satisfy
n , there are strings
v, w, x, y and z which satisfy
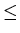 n
n
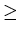 0 ,
vwmxymz
0 ,
vwmxymz  L
L