Regular Languages
Non-Regular Languages
Subjects to be Learned
- Existence of non-regular languages
- Myhill - Nerode Theorem for non-regularity test
- Pumping Lemma
Contents
We have learned regular languages, their properties and their usefulness
for describing various systems. There are, however, languages that are not regular
and therefore require devices other than finite automata to recognize them.
In this section we are going to study some of the methods for testing
given languages for regularity and see some of the languages that are not regular.
The main idea behind these test methods is that finite automata have only finite amount of memory
in the form of states and that they can not distinguish
infinitely many strings. For example to recognize the language
{ anbn | n is a natural number} ,
a finite automaton must remember how many a's it has read when it starts reading b's.
Thus it must be in different states when it has read different number of a's and starts
reading the first b. But any finite automaton has only finite number of states.
Thus there is no way for a finite automaton to remember how many a's it has read
for all possible strings anbn .
That is the main limitation of finite automata. Since a regular language must be recognized
by a finite automaton, we can conclude that
{ anbn | n is a natural number} is not regular.
This is the basis of
two of the regularity test methods we are going to study below: Myhill-Nerode Theorem and Pumping Lemma.
Myhill-Nerode Theorm
Indistinguishability of strings:
Strings x and y in  *
are indistinguishable with respect to a language L
if and only if
for every string z in
*
are indistinguishable with respect to a language L
if and only if
for every string z in  *, either xz and yz are both
in L or they are both not in L.
*, either xz and yz are both
in L or they are both not in L.
For example, a and aa are indistinguishable with respect to the language an
over alphabet { a }, where n is a positive integer, because aak and
aaak
are in the language an for any positive integer k. However, with respect to
the language
anbn , a and aa are
not indistinguishable (hence distinguishable), because ab is in the language anbn
while aab is not in the language.
Using this concept of indistinguishability, the following theorem by Myhill and Nerod
gives a criterion for (non)regularity of a language. It is stated without a proof.
Myhill-Nerode Theorem :
A language L over alphabet  is nonregular
if and only if there is an infinite subset of
is nonregular
if and only if there is an infinite subset of  * ,
whose strings are pairwise
distinguishable with respect to L.
* ,
whose strings are pairwise
distinguishable with respect to L.
Example 1:
L1 = { anbn | n is a positive integer } over alphabet
{ a , b } can be shown
to be nonregular using Myhill-Nerode as follows:
Consider the set of strings S1 = { an | n is a positive integer } .
S1 is over alphabet { a , b } and it is infinite. We are going to show that
its strings are pairwise distinguishable
with respect to L1. Let ak and am be arbitrary two different
members of the set S1, where k and m are
positive integers and k 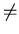 m .
Select bm as a string to be appended to ak and am . Then
akbm is not in L1 while
ambm is in L1 . Hence ak and am are
distinguishable with respect to L1 . Since
ak and am are arbitrary strings of S1,
S1 satisfies the conditions of Myhill-Nerode theorem. Hence L1 is
nonregular.
m .
Select bm as a string to be appended to ak and am . Then
akbm is not in L1 while
ambm is in L1 . Hence ak and am are
distinguishable with respect to L1 . Since
ak and am are arbitrary strings of S1,
S1 satisfies the conditions of Myhill-Nerode theorem. Hence L1 is
nonregular.
Example 2:
L2 = { ww | w  {a, b }* }
is nonregular.
{a, b }* }
is nonregular.
Consider the set of strings S2 which is the same as S1 of Example 1 above. It can be shown to be pairwise distinguishable with respect to L2 as follows.
Let ak and am be arbitrary two different members of the set, where k and m are
positive integers and k 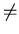 m .
Select bakb as a string to be appended to ak and am . Then
akbakb is in L2 while
ambakb is not in L2 . Hence ak and am
are distinguishable with respect to L2 . Since
ak and am are arbitrary strings of S2,
S2 satisfies the conditions of Myhill-Nerode theorem. Hence L2 is
nonregular.
m .
Select bakb as a string to be appended to ak and am . Then
akbakb is in L2 while
ambakb is not in L2 . Hence ak and am
are distinguishable with respect to L2 . Since
ak and am are arbitrary strings of S2,
S2 satisfies the conditions of Myhill-Nerode theorem. Hence L2 is
nonregular.
Example 3:
Let L3 be the set of algebraic expressions involving identifiers x and y, operations
+ and * and left and right parentheses.
L3 can be defined recursively as follows:
Basis Clause: x and y are in L3 .
Inductive Clause: If  and
and
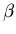 are in L3 , then
(
are in L3 , then
(  +
+ 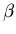 )
and (
)
and (  *
* 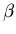 ) are in L3 .
) are in L3 .
Extremal Clause: Nothing is in L3 unless it is obtained from the above
two clauses.
For example, x , (x*y) , ( ( x + y ) * x ) and (( (x*y) + x ) + (y*y) ) are algebraic
expressions.
Consider the set of strings S3 = { (k x | k is a positive integer } ,
that is, the set of strings consisting of one or more right parentheses followed by
identifier x.
This set is infinite and it can be shown to be pairwise distinguishable with respect
to L3 as follows:
Let (k x and (m x be arbitrary two strings of S3 ,
where k and m are positive integers and k 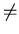 m .
Select [ + x ) ]k
as a string to be appended to (k and (m .
For example [ + x ) ]3 is +x)+x)+x) .
m .
Select [ + x ) ]k
as a string to be appended to (k and (m .
For example [ + x ) ]3 is +x)+x)+x) .
Then (k x + [ + x ) ]k is in L3 but
(m x + [ + x ) ]k is not in L3 because
the number of ('s is not equal to the number of )'s in the latter string.
Hence S3 is pairwise distinguishable with respect to L3 .
Hence L3 is not regular.
Pumping Lemma
Let us consider the NFA given below.
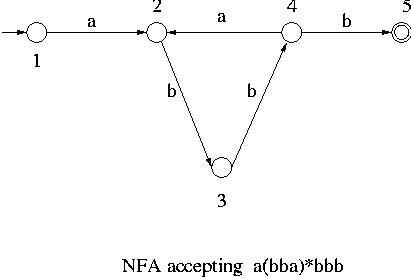
This NFA accepts among others some strings of length greater than 5 such as abbabbb,
abbabbabbb etc.
Those strings which are accepted by this NFA and whose length is greater than 5
have a substring which can be repeated any number of times without being rejected
by the NFA. For example the string abbabbb is accepted by the NFA and if one of its
substrings
bba is repeated any number of times in abbabbb, the resultant strings such as
abbb (bba repeated 0 times), abbabbabbb, abbabbabbabbb etc. are also accepted by the NFA.
In general if a string w (such as abbabbb in the example above) is accepted by an NFA
with n states and if its length is
longer than n, then there must be a cycle in the NFA along some path from the
initial state to some accepting state (such as the cycle 2-3-4-2 in the above example).
Then the substring representing that cycle (bba in the example) can be
repeated any number of times within the string w without being rejected by the NFA.
The following theorem which is called Pumping Lemma is based on this observation. It states
that if a language is regular, then any long enough string of the language has a substring
which can be repeated any number of times with the resultant strings still in the language.
It is stated without a proof here.
Pumping Lemma :
Suppose that a language L is regular. Then there is a positive integer n such that
for any string x in L with |x| 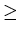 n, there are
strings u, v and w which satisfy the following relationships:
n, there are
strings u, v and w which satisfy the following relationships:
x = uvw
|uv| 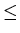 n
n
|v| > 0 and
for every integer m 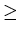 0, uvmw
0, uvmw
 L.
L.
Note that Pumping Lemma gives a necessity for regular languages
and that it is not a sufficiency, that is, even if there is an integer n
that satisfies the conditions of Pumping Lemma, the language is not necessarily regular.
Thus Pumping Lemma can not be used to prove the regularity of a language. It can only show
that a language is nonregular.
Example 4:
As an example to illustrate how Pumping Lemma might be used to prove that
a language is nonregular, let us prove that the language
L = akbk is nonregular, where k is a natural number.
Suppose that L is regular. Then there is a positive integer n that satisfies the conditions
of Pumping Lemma. Consider a string x = anbn for that n.
Then there must be strings u, v, and w
such that
x = uvw,
|uv| 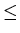 n
n
|v| > 0 , and
for every m 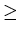 0, uvmw
0, uvmw
 L.
L.
Since |v| > 0 , v has at least one symbol. In string x = anbn,
v can be inside an , inside bn
or straddle an and bn .
Hence there are the following three possibilities for v:
1. v = ap, p > 0 ,
2. v = bp, p > 0 or
3. v = apbq , p, q > 0 .
Let us now consider the string uvmw for m = 2 for each of these three cases.
In case 1, uv2w = an-pa2pbn
= an+pbn . Since p > 0 , n + p
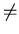 n . Hence
an+pbn can not be in the language L represented by
akbk .
n . Hence
an+pbn can not be in the language L represented by
akbk .
Similarly in case 2, since uv2w = an bn + p ,
it can not be in L.
In case 3, uv2w =
an-p(apbq)2bn-q =
an-p(apbqapbq)bn-q =
an bqapbn , which can not be in L.
Thus in all three cases uv2w is not in L. This violates the condition that
for every m 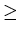 0, uvmw
0, uvmw
 L.
Hence L is not a regular language.
L.
Hence L is not a regular language.
Test Your Understanding of Non-regularity
Indicate which of the following statements are correct and which are not.
Click True or Fals , then Submit.
Next -- Context-Free Grammar
Back to Study Schedule
Back to Table of Contents
 *
are indistinguishable with respect to a language L
if and only if
for every string z in
*
are indistinguishable with respect to a language L
if and only if
for every string z in  *, either xz and yz are both
in L or they are both not in L.
*, either xz and yz are both
in L or they are both not in L.
 is nonregular
if and only if there is an infinite subset of
is nonregular
if and only if there is an infinite subset of  * ,
whose strings are pairwise
distinguishable with respect to L.
* ,
whose strings are pairwise
distinguishable with respect to L.
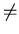 m .
Select bm as a string to be appended to ak and am . Then
akbm is not in L1 while
ambm is in L1 . Hence ak and am are
distinguishable with respect to L1 . Since
ak and am are arbitrary strings of S1,
S1 satisfies the conditions of Myhill-Nerode theorem. Hence L1 is
nonregular.
m .
Select bm as a string to be appended to ak and am . Then
akbm is not in L1 while
ambm is in L1 . Hence ak and am are
distinguishable with respect to L1 . Since
ak and am are arbitrary strings of S1,
S1 satisfies the conditions of Myhill-Nerode theorem. Hence L1 is
nonregular.
 {a, b }* }
is nonregular.
{a, b }* }
is nonregular.
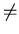 m .
Select bakb as a string to be appended to ak and am . Then
akbakb is in L2 while
ambakb is not in L2 . Hence ak and am
are distinguishable with respect to L2 . Since
ak and am are arbitrary strings of S2,
S2 satisfies the conditions of Myhill-Nerode theorem. Hence L2 is
nonregular.
m .
Select bakb as a string to be appended to ak and am . Then
akbakb is in L2 while
ambakb is not in L2 . Hence ak and am
are distinguishable with respect to L2 . Since
ak and am are arbitrary strings of S2,
S2 satisfies the conditions of Myhill-Nerode theorem. Hence L2 is
nonregular.
 and
and
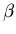 are in L3 , then
(
are in L3 , then
(  +
+ 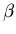 )
and (
)
and (  *
* 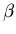 ) are in L3 .
) are in L3 .
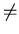 m .
Select [ + x ) ]k
as a string to be appended to (k and (m .
For example [ + x ) ]3 is +x)+x)+x) .
m .
Select [ + x ) ]k
as a string to be appended to (k and (m .
For example [ + x ) ]3 is +x)+x)+x) .

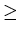 n, there are
strings u, v and w which satisfy the following relationships:
n, there are
strings u, v and w which satisfy the following relationships:
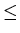 n
n
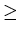 0, uvmw
0, uvmw
 L.
L.
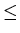 n
n
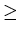 0, uvmw
0, uvmw
 L.
L.
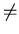 n . Hence
an+pbn can not be in the language L represented by
akbk .
n . Hence
an+pbn can not be in the language L represented by
akbk .
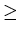 0, uvmw
0, uvmw
 L.
Hence L is not a regular language.
L.
Hence L is not a regular language.