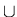 {x}.Therefore 0+ = 0
{x}.Therefore 0+ = 0 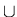 {0} = {0}
which is denoted as 1. Then 1+ = 1
{0} = {0}
which is denoted as 1. Then 1+ = 1 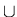 {1} = {0, 1} = {0}
{1} = {0, 1} = {0} 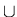 {{0}} = {0,
{0}} which is denoted as 2. 2+ = 2
{{0}} = {0,
{0}} which is denoted as 2. 2+ = 2 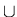 {2} = {0, 1}
{2} = {0, 1} 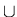 {2} = {0, 1, 2} = {0, {0}, {0,
{0}}}, which is dented as 3 etc.
{2} = {0, 1, 2} = {0, {0}, {0,
{0}}}, which is dented as 3 etc.
S
Naive Set Theory vs Axiomatic Set Theory
As given in Introduction to Set Theory of this course material, the concept of set is not defined rigorously in the naive set thoery which was originated by Georg Cantor. There we rely on everyone's notion of "set" as a collection of objects or a container of objects. In that sense "set " is an undefined concept. Similarly we say an object "belongs to " or "is a member of" a set without rigorously defining what it means. It is also assumed that sets have certain (obvious) properties usually asssociated with a collection of objects such as the union of sets exists, for any pair of sets there is a set that contains them etc. For example, P. Halmos lists those properties as axioms in his book "Naive Set Theory" as follows:
1. Axiom of extension
Two sets are equal if and only if they have the same elements.
For example {1, 2} = {1, 2, 1} because every element of {1, 2} is in {1, 2, 1} and vice versa.
2. Axiom of specification
For every set S and every proposition P, there is a set which contains those elements of S which satisfy P and nothing else.
For example let S be the set of natural numbers and let P be the proposition that states for every object x that x is an even number. Then this axiom states that there is a set that contains all the even natural numbers.
3. Axiom of pairs
For any two sets there is a set which contain both of them and nothing else.
For example for sets {1} and {1,2} there is a set that contains both of them. For example {{1}, {1,2}} is such a set in fact that is the only such set.
4. Axiom of union
For every collection of sets, there is a set that contains all the elements and only those that belong to at least one set in the collection.
For example for every natural number i let Ai = {20, 21 , 22, ..., 2i}. Then there is a set that contains all the powers of 2 and only those, that is {20, 21 , 22, ..., 2i, ...}.
5. Axiom of powers.
For each set A there is a collection of sets that contains all the subsets of the set A and nothing else.
For example a set that contains all the subsets of the set of natural numbers exists, that is there is a set that contains all the sets of natural numbers.
6. Axiom of infinity
There is a set containing 0 and the successor of each of its elements.
Here 0 is defined to be the empty set and the successor of
an element x , denoted by x+, is the set obtained by adding element
x to the set x i.e. x+ = x 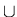 {x}.Therefore 0+ = 0
{x}.Therefore 0+ = 0 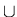 {0} = {0}
which is denoted as 1. Then 1+ = 1
{0} = {0}
which is denoted as 1. Then 1+ = 1  {1} = {0, 1} = {0}
{1} = {0, 1} = {0}  {{0}} = {0,
{0}} which is denoted as 2. 2+ = 2
{{0}} = {0,
{0}} which is denoted as 2. 2+ = 2  {2} = {0, 1}
{2} = {0, 1}  {2} = {0, 1, 2} = {0, {0}, {0,
{0}}}, which is dented as 3 etc.
{2} = {0, 1, 2} = {0, {0}, {0,
{0}}}, which is dented as 3 etc.
Thus a set containing 0 and the successor of each of its elements contains 0, 1, 2, 3, ... and possibly some more. Such sets can be employed to rigorously describe the concept of infinity. The smallest of such set is defined to be the set of natural numbers and an element of that set is a natural number.
7. Axiom of choice
The Cartesian product of a non-empty indexed collection of non-empty sets is non-empty. In other words if {Ai} is a collection of non-empty sets indexed by a non-empty set I, then there is an indexed collection {xi} such that xi is an element of Ai for each i in I.
For example for every natural number i let Ai = {20, 21 , 22, ..., 2i}. Then {A0, A1, A2, ...} is a collection of infinitely many non-empty sets. The axiom of choice guarantees that we can choose an element from each of these Ai 's simultaneously. This axim guarantees simultaneous choice of elements from an infinite as well as finite collection of sets.
Using those properties a naive set theory develops concepts of ordered pair, relation, and function, and discusses their properties, which are basically followed in the course material for this course. It further discusses numbers, cardinals, ordinals, their arithmetics, and finally different kinds of infinity, in particular uncountability of the set of real numbers.
In the naive set theory originated by Cantor the concept of set was not defined. In particular no attention was paid to the nature of elements of sets. Since a set is understood to be a collection of objects, it was assumed that any object can be a member of a set. However, Russell's paradox showed that that was not the case, that is, not every object can be a member of a set. The paradox proceeds as follows:
Let S = { x : x is set and x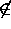 x }. Then since anything can be in a set, S is a set.
x }. Then since anything can be in a set, S is a set.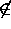 S or S
S or S  S. If S
S. If S 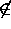 S, then by the definition of S, S
S, then by the definition of S, S  S, which is a contradiction. Thus S
S, which is a contradiction. Thus S  S.
However, then again by the definition of S, S
S.
However, then again by the definition of S, S 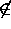 S, which is also a contradiction. Thus S can not be a set. That is, there are objects which can not be in a set.
S, which is also a contradiction. Thus S can not be a set. That is, there are objects which can not be in a set.