Properties of Regular Languages
CS390, Spring 2024
Abstract
In the previous modules, we have seen two very different ways to describe regular languages: by giving a FA or by a regular expression.
In this section we focus on the important properties of the languages themselves. We will look at decision procedures, which allow us to decide questions about regular languages. We will also look at the problem of minimizing DFAs, reducing a DFA to the smallest possible number of states without changing the language it recognizes.
We start, in this lesson, with important tools for checking whether a language is regular:
- The Pumping Lemma, a useful tool for proving that certain languages are not regular.
- Closure properties, which can help to identify languages that are regular.
1 The Pumping Lemma
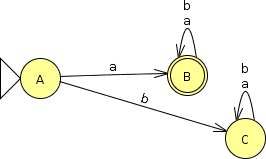
The FA on the right accepts strings over $\{a, b\}$ that start with ‘a’. This illustrates that an FA can distinguish input strings based upon the opening symbols of its input.
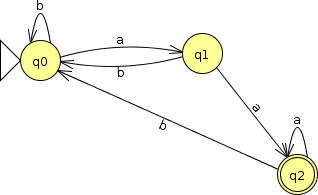
This FA, on the other hand, accepts strings over $\{a, b\}$ that end with ‘aa’. So FAs can also distinguish input strings based upon the closing symbols of their input.
If you are willing to set up enough states, you can use an FA to recognize any non-repeated pattern at the start and/or end of strings. But there are limits to how discriminating an FA can be “in between”.
1.1 The Lemma
Theorem 4.1: (The pumping lemma for regular languages)
Let $L$ be a regular language. Then there exists a constant $n$ (which depends on $L$) such that for every string $w$ in $L$ such that $|w| \geq n$, we can break $w$ into three strings, $w = xyz$, such that
- $y \ne \epsilon$
- $|xy| \leq n$, and
- $\forall k \geq 0$, the string $xy^kz$ is also in $L$.
 (video)
(video)The Pumping Lemma basically indicates that a FA can distinguish based upon some initial input symbols and also upon some closing input symbols, but because it has only a finite number of states it cannot “remember” everything that goes on in the middle. It must “loop” repeatedly back to the same state(s) in the middle of the input. (This is somewhat reminiscent of the argument we made in converting FAs to regular expressions.)
1.2 Using the Pumping Lemma
The Pumping lemma is most useful as a way of proving that a language cannot possibly be accepted by an FA. The examples given in the book:
\[ L = \{x \in \{a,b\}^* | n_a(x) > n_b(x) \} \]
is a “classic” of CS theory.
1.2.1 $0^n1^n$
Also of note is this language:
\[ L = \{0^{n} 1^{n} | n \geq 1\} \]
which is suggested in exercise 4.1.1a.
These languages have a certain practical implication. If you cannot use an FA to determine to guarantee that two different characters occur the same number of times in a string, even if they are arranged conveniently with all of the occurrences of one character coming before any occurrences of the other, then you almost certainly cannot use an FA to solve the even more complicated problem of determining whether parentheses or brackets are balanced in a program. Such checks are, however, critical in compilers and other programming language processors. This tells us that the regular languages are not powerful enough to express some rather mundane characteristics of typical programming languages.
Let’s look at how we can use the Pumping Lemma to provide that this second language, $\{0^{n} 1^{n} | n \geq 1\}$, is not regular.
According to the Pumping Lemma, if this were regular, then every sufficiently long string in the language can be divided into three pieces, $x$, $y$, and $z$, such that $x y^* z$ is also in the language. Let $n$ be the critical value for this language. Then consider a string $s = 0^n1^n$ (which is clearly longer than $n$). The Pumping lemma says that, if this language is regular, we can divide this string into pieces $x$, $y$, and $z$ such that $|xy| \leq n$, $|y| > 0$, and all $xy^*z$ are also in the language.
Let’s try to divide that string into those pieces $x$, $y$, and $z$ such that $s = xyz$. There are two cases to consider:
-
$y$ contains only zeros. So, we have $x=0^i$, $y=0^j$, $j > 0$, $z=0^k1^n$, such that $i + j + k = n$. But the Pumping lemma says that $xy^2z$ would also need to be in the language. But $xy^2z = 0^{i+2j+k}1^n$. That string is in the language $0^n1^n$ only if $i + 2j + k = n$. Since
\[ i + j + k = n = i + 2j + k\]
has no solution when $j > 0$, this is not possible.
-
$y$ contains at least one ‘1’. But then $x$ must contain all of the 0’s (and possibly some 1’s), so $|xy| > n$, which also violates the Pumping Lemma.
Hence the Pumping Lemma tells us that $0^i1^i$ cannot be a regular language. (This is often used as a justification for the informal claim that a FA can only “remember” a finite amount of prior history of what has been input into it.)
1.2.2 # of zeros == # of ones
Can you use the Pumping Lemma to prove the following:
Prove that the language over {0,1} consisting of all strings with equal numbers of zeros and ones is not a regular language.
Think about this for a moment. The key idea, when applying the pumping lemma, is to identify a large string that is definitely in the language, but that cannot be divided into sections such that the middle part can be repeated indefinitely while staying in the language. If you can identify such a string, everything else follows form there.
2 Closure Properties
We say that a set $S$ is closed under a binary operation $\oplus$ iff $\forall a \in S, b \in S \Rightarrow a \oplus b \in S$. That is, pick any two elements of $S$ and apply the operator to them and the result is also in $S$.
- We can do similar definitions for closure of a set under operators that take 1, 3, or any greater number of operands.
Example 1: Familiar ClosuresThe set of integers, $\cal{Z}$, is closed under addition, because for any two integers $i$ and $j$, $i + j$ is still an integer. Similarly, the set of integers is closed under subtraction and multiplication.
The set of natural numbers, $\cal{N}$, on the other hand, is not closed under subtraction. We can prove this by example: 2 and 5 are both natural numbers, but $2 - 5$ is negative and therefore not a natural number.
In this section, we are interested in the kinds of operations that we can perform on Regular Languages and still be guaranteed that we will get a regular Language as a result.
2.1 Closure Under Set Operations
Languages are sets of strings, and it is natural to think of the common set operations such as union, intersection, etc., as ways to combine languages. Clearly the set of all languages will be closed under any common set operations. The union/intersection/complement/difference of sets of strings will still yield a set of strings.
But do regular languages, the set of languages accepted by regular expressions and FAs, have the same kind of closure?
2.1.1 The Regular Languages are Closed under Union
We’ve actually already shown this by showing that, given a pair of FAs, we can easily construct an NFA that accepts the union of their languages.
Your text makes the equally simple argument that, given a pair of regular expressions $R_1$ and $R_2$, we can write $(R_1) + (R_2)$, which is still a regular expression and therefore still describes a regular language.
2.1.2 The Regular Languages are Closed under Complement
A complement of something, in English, is something “completes” that something. For example, you may be familiar with the idea that all colors of light can be broken down into red, blue and green components. So if you were designing an adjustable mood lighting system and you had a red bulb and a blue bulb, you might see that as incomplete. If someone then handed you a green bulb, you might say that it complements the other two bulbs. (Don’t confuse “complement” with “compliment”, to make encouraging statements about something.)
A complement of a set S would be the set T that “completes” S in the sense that $S \cup T$ is the entire universe of set elements, and $S \cap T = \emptyset$, there is no overlap between $S$ and $T$.
For a language $L$, a complement would be the set of strings in the same universe ($\Sigma^*$) that are not members of $L$.
It’s not hard to show that regular languages are closed under complements.

Take any DFA for a regular language L. For example, this DFA for the language of strings over alphabet $\{a, b\}$ that end with “aa”. Suppose we want to take $\bar{L}$, the set of all strings over that same alphabet that do not end with “aa”.
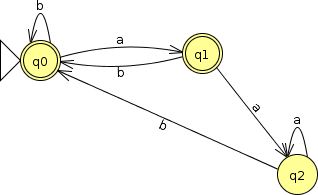
That’s pretty easy to do with a DFA — just exchange all of the final and non-final states. Clearly the resulting FSA will accept exactly the strings that the original DFA would not have accepted.
One of the interesting things about this construction is that it’s so easy to with FAs, but trying to write a regular expression that accepts the complement of the language accepted by another regular expression can be quite tricky.
2.1.3 The Regular Languages are Closed under Intersection
One way to prove this is to modify our argument for closure under union.
- Start with our earlier construction for running two FAs “in parallel”.
- Then convert that NFA into a DFA. The resulting DFA will be labeled with sets of labels from the original two FAs, representing states that could be simultaneously active when we ran those FAs in parallel.
-
Choose as final states in our new DFA only those states in which every label from the original FAs were final.
Alternatively, we can prove closure under intersection by reducing intersection to other operators:
\[ A \cap B = \overline{\bar{A} \cup \bar{B}} \]
and since, the regular languages are closed under union and complement, they must be closed under intersection as well.
2.1.4 The Regular Languages are Closed under Difference
Set difference selects all of the elements in one set that are not present in a second set. To show that the regular languages are closed under difference, we only have to note that
\[ A - B = A \cap \bar{B} \]
2.2 Other Closure Properties
2.2.1 The Regular Languages are Closed under Reversal
If we have a FA for a language $L$, we can construct an FA that accepts $L^R$ the set of strings that are reversed versions of some string in $L$.
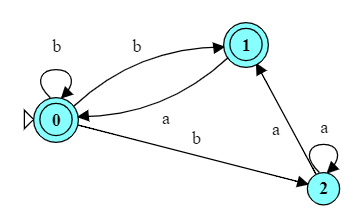
For example, if we start with this FA for strings over $\{a, b\}$ that do not end with “aa”,
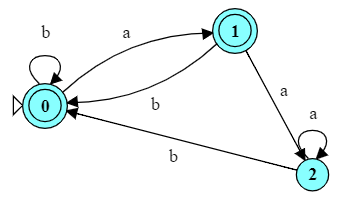
-
Reverse all of the arcs in the transition diagram.
If this leaves us with any states that lack a transition on some symbol of $\Sigma$, add a transition to a special, unescapable “trap” state.
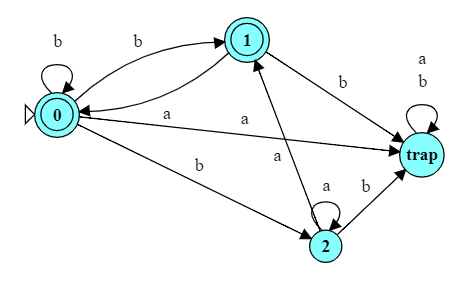
-
Make the start state the only accepting state.
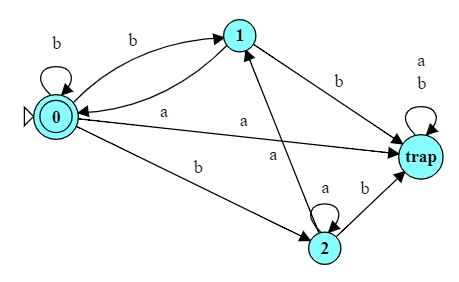
-
Create a new start state with transitions on $\epsilon$ to each of the original accepting states.
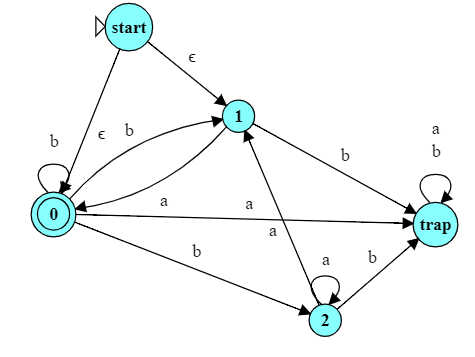
You may be able see that this automaton accepts all strings that do not begin with “aa” (i.e., that are reversed forms of strings that do not end in “aa”). If not, here is the reversed automaton in Automat. Try running this automaton and convince yourself that it works.
Could we do a simpler DFA than this? Certainly. Later we will discuss an algorithm for minimizing a DFA. But having done the construction is enough to demonstrate the closure.
Your text carries out the formal argument that this construction can be show in general to guarantee closure.
2.2.2 The Regular Languages are Closed under Homomorphism
A homomorphism in general is a transformation (“morph”) accomplished by a uniformly applied (“homo” as in “homogenous”) substitution.
In this context, we are considering the substitution of strings for characters in $\Sigma$.
Single-Character Substitutions
Now it should be obvious that, if we have a regular language $L$, we could substitute characters in $\Sigma$ by other single characters and still be regular.
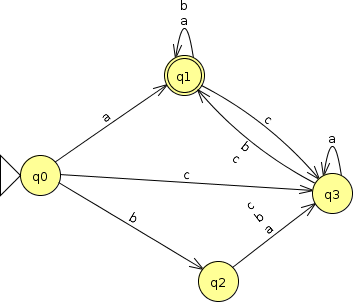
For example, if I show you this FA, you would have to agree that, whatever language it accepts, that language is regular.
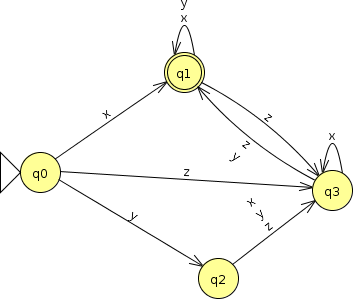
And, having said that, you might agree that if I replace ‘a’ by ‘x’, ‘b’ by ‘y’, and ‘c’ by ‘z’, the existence of the resulting FA proves that the language is still regular.
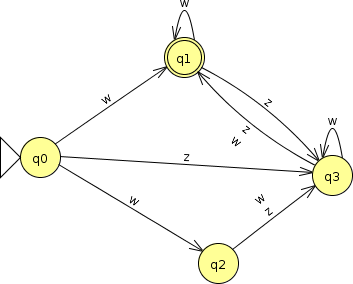
In fact, the replacement doesn’t even have to be one-to-one. If I replace ‘a’ and ‘b’ by ‘w’, and replace ‘c’ by ‘z’, the FA becomes non-deterministic, but it’s still an FA and so the language that it accepts is therefore still regular.
String Substitutions
OK, so single character homomorphisms preserve regularity. But what about replacing each character in the language by an entire string?
After all, if we wanted to replace ‘a’ by “cat” and ‘b’ by “dog”, we can’t go from
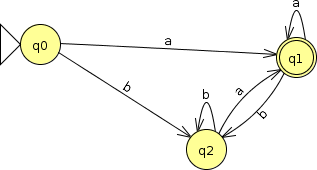
to
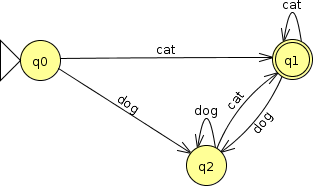
can we? That’s not a FA.
But we can do this: “Split” each of the original single-character arcs by introducing intermediate states.
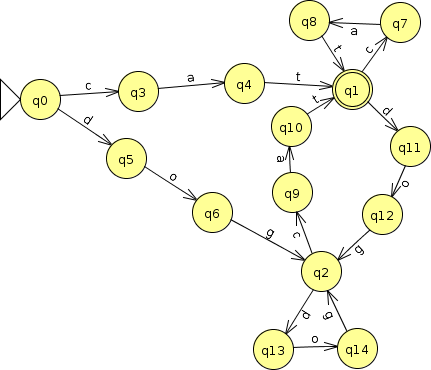
Your text formalizes this construction to prove the regular languages are closed under homomorphism.
2.2.3 The Regular Languages are Closed under Reverse Homomorphism
A reverse homomorphism replaces entire strings in a language by individual symbols. This is fairly easy to envision in a “set of strings” view, e.g., if I had a language of all strings ending in “aa”:
\[ \{ aa, aaa, baa, aaaa, abaa, baaa, bbaa, \ldots \} \]
and I decided to replace all strings “ba” by ‘w’, I would get
\[ \{ aa, aaa, wa, aaaa, awa, waa, bwa, \ldots \} \]
what I would be left with is still a language, but it’s hard to actually describe what’s in the language. If I had started with a FA or regular expression for the language, it would be hard to even describe the substitution.
Nonetheless, the regular languages are closed under this operation as well.

