Decision Problems for Regular Languages
CS390, Spring 2024
1 Decision procedures
Decision procedures are, in essence, algorithms that return a boolean true/false result. They typically represent questions that we might want to ask about a language. We would like to know if certain questions are decidable, if there is some systematic way of answering the question.
A decision procedure is an algorithm for computing the answer to such a problem. We frequently demonstrate that a problem is decidable by actually giving an algorithm for deciding it.
When we talk about “decision procedures” or “algorithms”, we refer to step-by-step procedures that are guaranteed to terminate with an answer.
You cannot, for example, answer the question is P decidable for any regular language L?“ by starting with ”make a list of all the strings in L“ or ”loop through all strings in L" because many regular languages (perhaps, most of the interesting ones) are infinite, so such a loop might not terminate.
Many decision procedures for regular languages work by treating an FA as a graph and applying common graph algorithms to it. If that doesn’t ring a bell, and particularly if you have not yet taken CS361, you might want to look at Graphs – the Basics and Traversing a Graph. You don’t really need anything more than the idea of traversing a graph, as that is enough to let you answer questions like “can I go from q0 to q12?” or “which states can I reach starting from q4?”, which are the kind of questions you need for most regular language decision problems.
1.1 Is a Regular Language Empty?
If someone shows us a regular language as a set of strings, this is trivially easy to answer. But we could ask the same question about a regular language presented to us in the form of an FA or a regular expression.
-
If we are given an FA, we only need to trace a path from the start state to any final state. If such a path exists, its transitions define a string in the language and we know that the language is not empty.
-
In algorithmic terms, we would do a depth-first-traversal starting from the initial state and stopping when we have reached a final state or have visited all states reachable from the initial state.
-
This would be our decision procedure to answer this question.
-
 (video)
(video)
-
-
If we are given a regular expression, we can convert it to an FA and then search that FA, as just described.
-
Again, we have a step-by-step, guaranteed-to-halt, procedure for doing this, so what we have described is a decision procedure whose very existence shows that the question is decidable.
-
1.2 Is the String s a Member of a Regular Language L?
-
If we are given an FA, we only need to “execute” the FA on the string $s$ and see if we end at an accepting state.
-
If we are given a regular expression, we can convert it to an FA and then execute that FA, as just described.
1.3 Distinguishable States
One of the most fundamental questions we might ask about regular languages is
Do two FAs describe the same language?
Before we can answer this question, we need to introduce an intermediate problem: given any two states in an FA, are those states equivalent or distinguishable?
We’ll say that two states $p$ and $q$ are equivalent if
-
Both are accepting or neither is accepting.
Formally, $p \in F \Leftrightarrow q \in F$.
-
If we feed any string $w$ into the FA starting from $p$ and then again starting from $q$, we wind up in states that match in acceptance states: both accept or neither does.
Formally,
\[ \forall w \in \Sigma^*, \hat{\delta}(p,w) \in F \Leftrightarrow \hat{\delta}(q,w) \in F \]
If two states are not equivalent, we say that they are distinguishable.
What does that really mean if we say that two states are distinguishable?
Numerous studies have shown that most people cannot distinguish the taste of one of the two most popular-selling cola brands from the other. If I were red-green color blind, I would be unable to distinguish red objects from green ones. At night, most of us cannot distinguish blue objects from green ones. I have a relative who is tone-deaf. She cannot distinguish the musical pitch C from the neighboring D.
So what does it mean when we talk about a state or an FA not being able to distinguish one string from another? It means that it cannot tell them apart, no matter what we do in the way of further inspection.
 (video)
(video)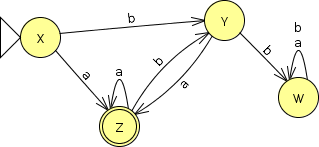
For example, consider this FA for the language of strings in which every ‘b’ is followed immediately by an ‘a’. If I were to execute this on the strings “aaab” and “abba”, for example, winding up in states Y and W, respectively, both strings are “not accepted” as is.
So do we really need both W and Y in our FA? Yes. These are distinguishable by this language, because if I consider adding the string “a” to each of them, then “aaaba” is accepted but “abbaa” is still not accepted. So it is possible to tell those two states apart by feeding additional characters into the FA.
1.3.1 A Decision Procedure for Distinguishing States
We can determine which pairs of states in a DFA are distinguishable from others by a “table filling algorithm”.
- We set up a table mapping each state onto each other state.
- We make a first pass by marking all of the accepting states as distinguishable from the non-accepting states.
- Then the algorithm extends those sets of states that can be distinguished by taking each unmarked pair (q,r) that we have not analyzed yet and considering where we could go by inputting one more additional character.
If those would take us to a pair of states already know to be distinguished, then (q,r) are distinguished as well.
 (video)
(video)1.3.2 Distinguishability Example 1
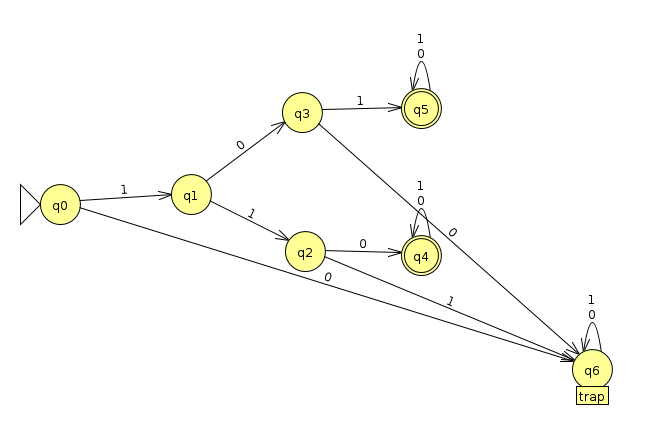
Which of the states in this DFA are distinguishble?
1.3.3 Distinguishability Example 2
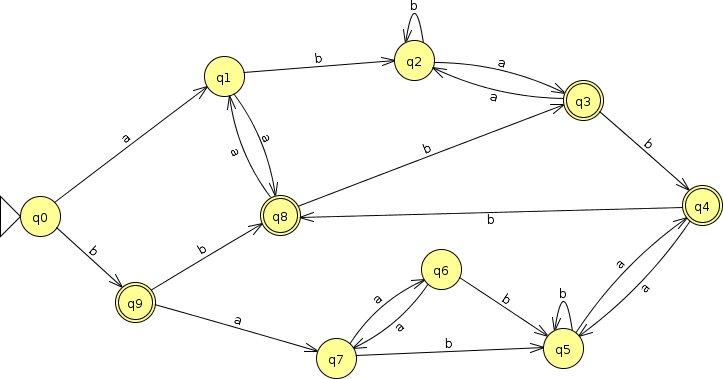
What are the distinguishable states in this FA?
1.4 Determining if Two FAs Accept the Same Language
With the ability to determine if two FAs are equivalent, we can now answer the question of whether two FAs accept the same language.
-
Pretend that we are going to run the two FSAs in parallel, much as we have done before.
We do this by creating a new starting state, and add $\epsilon$ trnasitions from it to the starting states of the original two FAs.
-
Do the table-filling algorithm.
- Check the starting states of the original FSAs in the final table. If they are marked as distinguished, that means that there exists at least one input string on which the two FSAs disagree over whether to accept that string. Thus they do not accept the same language. If the two states are unmarked and therefore equivalent, then no such string exists and the two FSAs agree on every possible input string, meaning that they accept the same language.
2 Minimizing States in a Finite Automaton
We can also make use of this idea of equivalent/distinguishable states to minimize the number of states in a DFA.
-
Start by determining which pairs of states are distinguishable as described above.
-
Look at the unmarked spaces in the final table. Those represent pairs of equivalent states. Equivalence is transitive. If A and B are equivalent, and B and C are equivalent, then A and C are equivalent.
Partition the set of states by taking the transitive closure of the state equivalence for each state.
In other words, gather together all the sets of states that are all equivalent to one another.
This yields multiple sets of states, with search set containing only states that are equivalent to one another.
-
Create an FA with a state for each set in that partition.
-
Trace the state transitions from each of these combined state for each symbol in $\Sigma$ to get the new transitions.
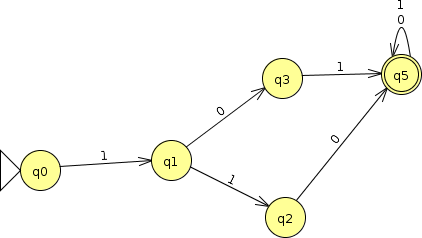
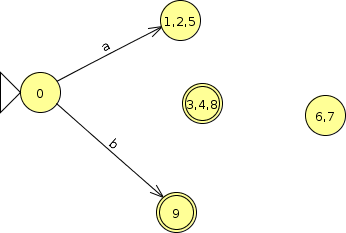
2.1 Minimization Example 1
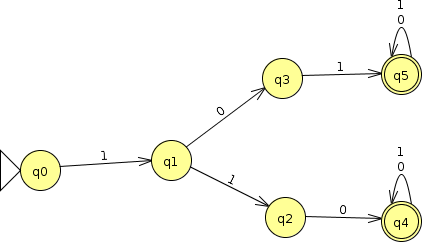
What is the smallest DFA accepting the same language as this FA?
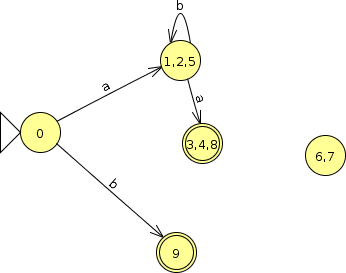
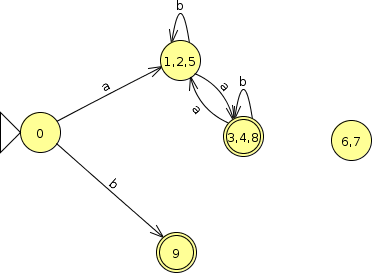
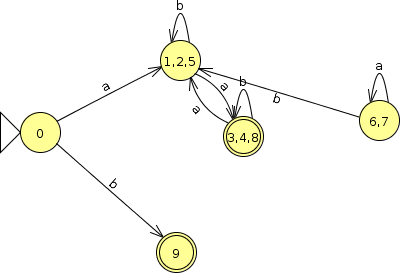
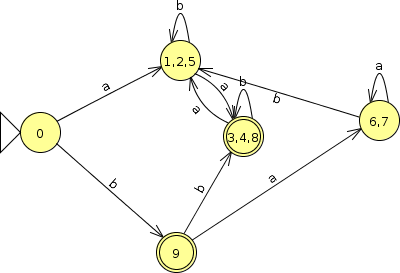
2.2 Minimization Example 2

What is the smallest FA accepting he same language as this one?